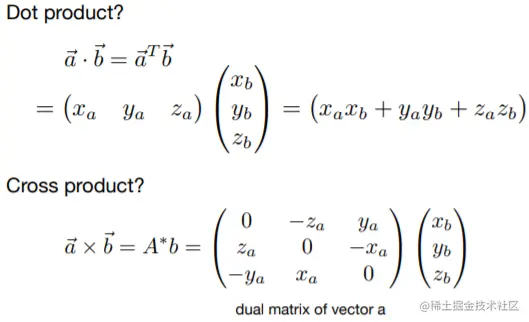Games101学习笔记#1 - 向量与线性代数

codeMan
460 阅读3分钟

课程地址

课程录像：GAMES101-现代计算机图形学入门-闫令琪
课程主页：GAMES101: 现代计算机图形学入门
本节PPT：GAMES101_Lecture_02
作业地址：往期作业汇总帖

1. 摘要

  • 向量（点乘、叉乘...）
  • 矩阵（矩阵与矩阵相乘、矩阵与向量相乘...）

2. 向量

  • 概念：表示一个方向和长度的量。
  • 用笛卡尔坐标系表示：有两个相互垂直的单位向量 x⃗\vec{x} 和 y⃗\vec{y}，任一个向量 a⃗\vec{a} 都可以表示为从原点开始的由m个 x⃗\vec{x} 向量与n个 y⃗\vec{y} 向量相加而成，这个(m,n)就表示向量 a⃗\vec{a}。
  • 在图形学中向量通常用列矩阵来表示（在后面的学习中，就会知道这是为了方便与矩阵进行运算）。

image.png

  • 点乘

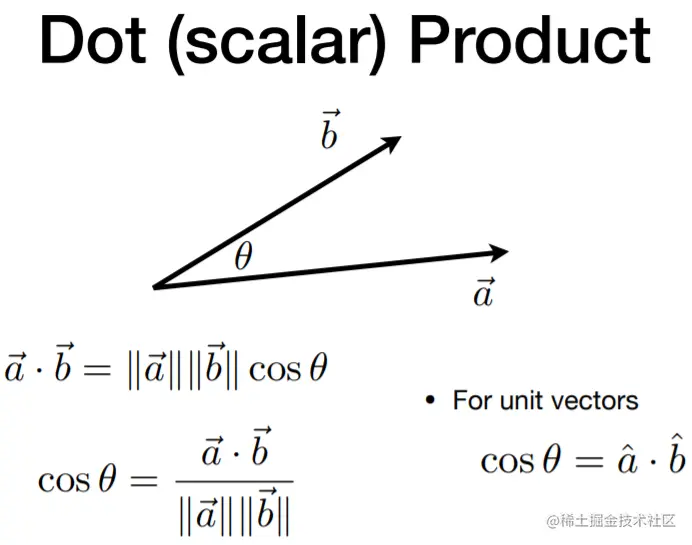
    • 定义：∥x⃗∥×∥y⃗∥×cos⁡θ\lVert\vec{x}\rVert \times \lVert\vec{y}\rVert \times \cos\theta

    • 作用：得到两个向量之间的夹角（尤其是对两个单位向量来说，点乘就是夹角余弦值）、将向量拆分成两个相关垂直的向量、两个向量在方向上有多接近。

    • 矩阵表示：将两个向量分别用列矩阵表示再相乘即可得到点乘值。

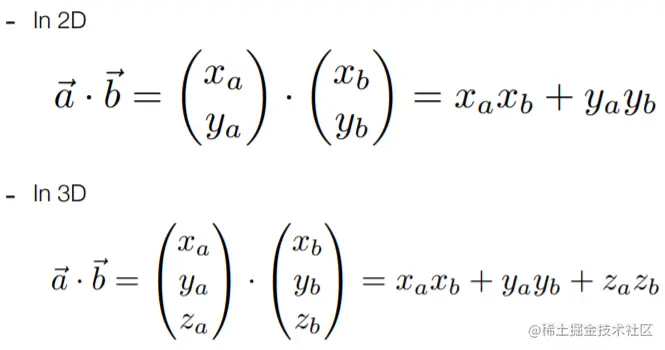
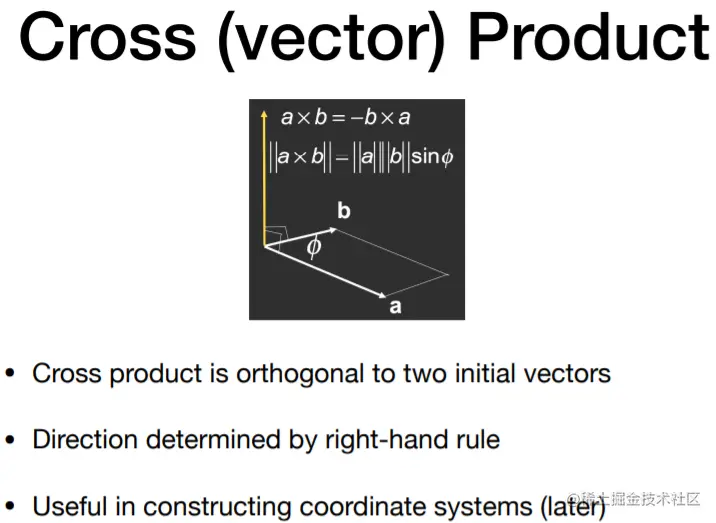
image.png

  • 叉乘
    • 定义：一个与向量a⃗\vec{a}和向量b⃗\vec{b}都垂直的向量c⃗\vec{c}，可以通过右手定则得到该向量的方向（将四个手指从a⃗\vec{a}向b⃗\vec{b}弯曲，拇指的朝向就是向量c⃗\vec{c}的方向）
    • 左手系和右手系区分：
      • 右手系：x⃗×y⃗=z⃗\vec{x}\times\vec{y}=\vec{z}
      • 左手系：x⃗×y⃗=−z⃗\vec{x}\times\vec{y}=-\vec{z}
    • 作用：

      • 判定左和右：在右手空间直角坐标系下，有两个在x⃗y⃗\vec{x}\vec{y}平面上的向量a⃗\vec{a}和b⃗\vec{b}。a⃗\vec{a}叉乘b⃗\vec{b}的方向是 z⃗\vec{z}，则 a⃗\vec{a} 在 b⃗\vec{b} 的右边；是−z⃗-\vec{z}，则 a⃗\vec{a} 在 b⃗\vec{b} 的左边。

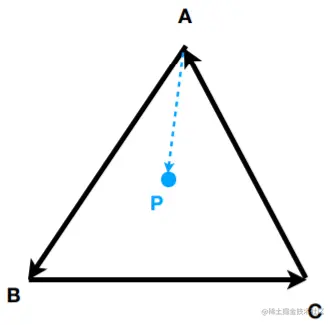
      • 判定内和外：分别计算AP⃗\vec{AP}和AB⃗\vec{AB}、BP⃗\vec{BP}和BC⃗\vec{BC}、CP⃗\vec{CP}和CA⃗\vec{CA}的叉乘，若三个结果的方向都一致，则P点在三角形ABC内，否则在三角形外。

      • 将任意一个向量分解到一个自定义的空间直角坐标系：假设有三个相互垂直的单位向量 u⃗\vec{u}、v⃗\vec{v}、w⃗\vec{w}（任意两个向量的点乘为0，且u⃗×v⃗\vec{u}\times\vec{v}=w⃗\vec{w}）,那么任意一个向量 p⃗\vec{p}，都可以表示为(p⃗⋅u⃗)u⃗+(p⃗⋅v⃗)v⃗+(p⃗⋅w⃗)w⃗(\vec{p}\cdot\vec{u})\vec{u}+(\vec{p}\cdot\vec{v})\vec{v}+(\vec{p}\cdot\vec{w})\vec{w}，即向量p⃗\vec{p} 在 u⃗v⃗w⃗\vec{u}\vec{v}\vec{w} 坐标系中的坐标为(p⃗⋅u⃗,p⃗⋅v⃗,p⃗⋅w⃗)(\vec{p}\cdot\vec{u},\vec{p}\cdot\vec{v},\vec{p}\cdot\vec{w})。

    • 矩阵表示：

image.png

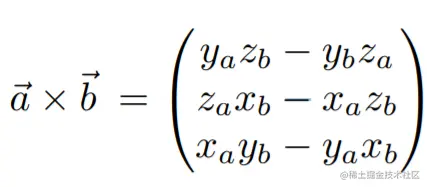
3. 矩阵

  • 概念：按照行列进行排布的数字集合。
  • 矩阵相乘
    • 运算条件：矩阵A与矩阵B相乘，那么A的列数一定等于B的行数
    • 运算结果：m×nm\times n矩阵与n×pn\times p矩阵的乘积为m×pm\times p矩阵，其中元素(i,j)(i,j)的值为第一个矩阵的第 ii 行与第二个矩阵的第 jj 行的点积。

image.png

  • 矩阵性质
    • 不满足交换律：AB≠BAAB\neq BA。
    • 满足结合律和分配律。
    • 主要性质：可以改变运算先后，但不能改变左右运算顺序。 image.png
  • 矩阵转置
    • 定义：行列互换，(i,j)(i,j) 变为 (j,i)(j,i)。
    • 性质：(AB)T=BTAT(AB)^\mathrm{T} = B^\mathrm{T}A^\mathrm{T}。
    image.png
  • 单位矩阵
    • 定义：只有对角线上的值为1，其他值为0的矩阵。
    • 矩阵的逆：一个矩阵与矩阵A的乘积为单位矩阵，那么这个矩阵就是A的逆，记为A−1A^{-1}。
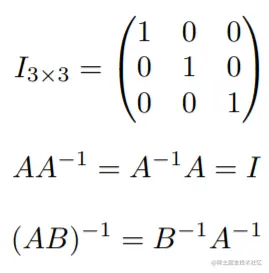
    • 逆的性质：(AB)−1=B−1A−1(AB)^{-1} = B^{-1}A^{-1}。 image.png
  • 用矩阵计算点乘和叉乘（向量由列矩阵表示）
    • 点乘：a⃗⋅b⃗=a⃗Tb⃗\vec{a}\cdot\vec{b}=\vec{a}^\mathrm{T}\vec{b}。
    • 叉乘：a⃗×b⃗=A∗b\vec{a}\times\vec{b}=A^*b。注：A∗A^*是由 a⃗\vec{a} 按照一定规律转换而成的矩阵。 image.png
avatar
文章
阅读
粉丝