本文已参与「新人创作礼」活动，一起开启掘金创作之路。

每日一题做题记录，参考官方和三叶的题解

题目要求

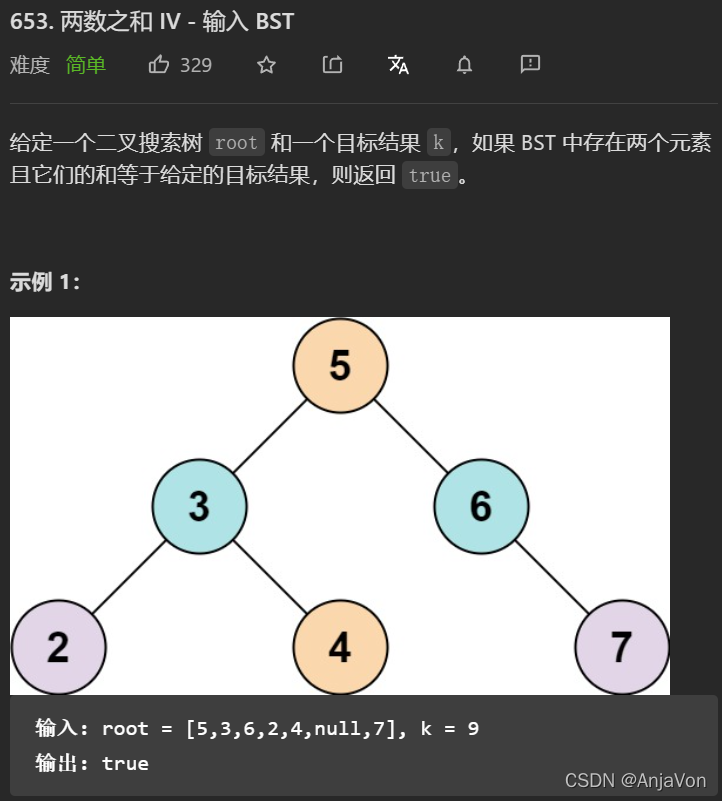
思路一：DFS

用DFS遍历整棵树，并用哈希表set存储遍历过的值，查找set是否有与当前值相加得到目标的值。
两种语言的哈希表分别为HashSet和unordered_Set，在19日的题目中也有使用。

Java

class Solution {
    Set<Integer> set = new HashSet<>();
    public boolean findTarget(TreeNode root, int k) {
        if(root == null)
            return false;
        if(set.contains(k - root.val))
            return true;
        set.add(root.val);
        return findTarget(root.left, k) | findTarget(root.right, k);
    }
}

• 时间复杂度：$O(n)$，$n$为BST的大小
• 空间复杂度：$O(n)$

C++

class Solution {
public:
    unordered_set<int> set;
    bool findTarget(TreeNode* root, int k) {
        if(root == nullptr)
            return false;
        if(set.count(k - root -> val))
            return true;
        set.emplace(root -> val);
        return findTarget(root -> left, k) || findTarget(root -> right, k);
    }
};

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

emplace与insert

• 学习参考链接
• c++ 11中的多数容器都增加了一个新的插入元素函数方法emplace，简单来说它具有较高的效率，可以替代大部分的insert操作，原理在于其无需临时变量和隐式转换。

思路二：中序遍历+双指针

利用一下BST中序输出有序的特征，然后用双指针移动查找。
利用两个栈存放符合当前条件的较小值和较大值，栈顶元素分别是符合当前条件的最小值和最大值，也即BST中的“最”左值和“最”右值。

Java

class Solution {
    public boolean findTarget(TreeNode root, int k) {
        Deque<TreeNode> ls = new ArrayDeque<>(), rs = new ArrayDeque<>();//定义两个栈
        TreeNode tmp = root;
        //分别存放根左和根右
        while(tmp != null) {
            ls.addLast(tmp);
            tmp = tmp.left;
        }
        tmp = root;
        while(tmp != null) {
            rs.addLast(tmp);
            tmp = tmp.right;
        }
        //从最左（小）和最右（大）开始查找
        TreeNode l = ls.peekLast(), r = rs.peekLast();
        while(l.val < r.val) {
            int t = l.val + r.val;
            if(t == k)
                return true;
            else if(t < k) //小则向右找
                l = getNext(ls, true);
            else //大则向左找
                r = getNext(rs, false);    
        }
        return false;
    }

    TreeNode getNext(Deque<TreeNode> s, boolean isLeft) {
        TreeNode cur = s.pollLast();
        //找比cur大or小一点的值
        //找比cur右or左一点的值
        TreeNode node = isLeft ? cur.right : cur.left;
        while(node != null) {
            s.addLast(node);
            node = isLeft ? node.left : node.right;
        }
        return s.peekLast();
    }
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

ArrayDeque

• 学习参考链接
• 简介
  • 一个两端皆可插入/删除的队列
  • 简单区别一下peek和poll

方法	功能
addLast(key)	将key加入队尾
peekLast(key)	返回队尾元素key ，不删除

C++

注意指针地址符不要少，写java写习惯了导致调了好久。

class Solution {
public:
    bool findTarget(TreeNode* root, int k) {
        stack<TreeNode *> ls, rs; //定义两个栈
        TreeNode *tmp = root;
        //分别存放根左和根右
        while(tmp != nullptr) {
            ls.push(tmp);
            tmp = tmp->left;
        }
        tmp = root;
        while(tmp != nullptr) {
            rs.push(tmp);
            tmp = tmp->right;
        }
        //从最左（小）和最右（大）开始查找
        TreeNode *l = ls.top(), *r = rs.top();
        while(l->val < r->val) {
            int t = l->val + r->val;
            if(t == k)
                return true;
            else if(t < k) //小则向右找
                l = getNext(ls, true);
            else //大则向左找
                r = getNext(rs, false);
        }
        return false;
    }
    TreeNode *getNext(stack<TreeNode *> &s, bool isLeft) {
        TreeNode *cur = s.top();
        s.pop();
        //找比cur大or小一点的值
        //找比cur右or左一点的值
        TreeNode *node = isLeft ? cur->right : cur->left;
        while(node != nullptr) {
            s.push(node);
            node = isLeft ? node->left : node->right;
        }
        return s.top();
    }
};

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

总结

本题属于简单“树”类题目，直接套用DFS即可解决（BFS也一样），但是要想到如何利用二叉搜索树的特点并不简单，法二的思路值得多多琢磨。

欢迎指正与讨论！