关于周志华老师的《机器学习》这本书的学习笔记
记录学习过程
本博客记录Chapter9

1 聚类任务

聚类任务（clustering）是一类典型的”无监督学习“任务，其训练样本的标记信息是未知的，目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律：将数据集中的样本划分为若干个通常是互不相交的子集，每个子集称为一个簇。

形式化地说，假定样本集 $D=\{x_1,x_2,…,x_m\}$ 包含 $m$ 个无标记样本，每个样本 $x_i=(x_{i1},x_{i2},…,x_{in})$ 是一个 $n$ 维地特征向量。则聚类算法将样本集 $D$ 划分为 $k$ 个不相交的簇 $\{C_l|l=1,2,…,k\}$ 。我们用 $\lambda_j\in \{1,2,…,k\}$ 表示样本 $x_j$ 的”簇标记“（cluster label），即 $x_j \in C_{\lambda_j}$ 。于是聚类的结果可以用包含 $m$ 个元素的簇标记向量 $\lambda = \{\lambda_1,\lambda_2,…,\lambda_j\}$ 表示。

2 性能度量

聚类性能度量亦称为”有效性指标“（validity index）。针对聚类问题，直观上看，我们希望”物以类聚“，即同一簇的样本尽可能彼此相似，不同簇的样本尽可能不同。换言之，聚类结果的”簇内相似度“应该比较高，并且”簇间相似度“应该比较低。

聚类性能度量的指标大致有两类：

外部指标（external index）：将聚类结果与某个参考模型（reference model）进行比较
内部指标（internal index）：直接考察聚类结果而不利用任何参考模型

对于数据集 $D=\{x_1,x_2,…,x_m\}$ ，假定通过聚类得出的簇划分为 $C=\{C_1,C_2,…,C_k\}$ ，参考模型给出的簇划分 $C^*=\{C_1^*,C_2^*,…,C_s^*\}$ ，相应的，令 $\lambda$ 与 $\lambda^*$ 表示 $C$ 与 $C^*$ 的簇标记向量。我们将样本两两配对考虑，定义：

a=|SS|, \space\space SS=\{(x_i,x_j)|\lambda_i=\lambda_j,\lambda^*_i=\lambda_j^*,i<j\},\\ b=|SD|, \space\space SD=\{(x_i,x_j)|\lambda_i=\lambda_j,\lambda^*_i\neq \lambda_j^*,i<j\},\\ c=|DS|, \space\space DS=\{(x_i,x_j)|\lambda_i\neq \lambda_j,\lambda^*_i=\lambda_j^*,i<j\},\\ d=|DD|, \space\space DD=\{(x_i,x_j)|\lambda_i\neq \lambda_j,\lambda^*_i\neq \lambda_j^*,i<j\}

其中， $SS$ 表示了在 $C$ 中隶属于相同簇且在 $C^*$ 中也属于相同簇的样本对，其他类似……

由于每个样本对只能出现在其中一种情况，则有 $a+b+c+d=\frac{m(m-1)}{2}$

基于上述四个式子，我们可以推导出下面常用的聚类性能度量外部指标：

Jaccard系数
$JC=\frac{a}{a+b+c}$
FM指数
$FMI=\sqrt{\frac{a}{a+b}\cdot \frac{a}{a+c}}$
Rand指数
$RI=\frac{2(a+d)}{m(m-1)}$

上述三个外部指标的结果均在 $[0,1]$ 之间，值越大越好。

考虑聚类结果的簇划分 $C=\{C_1,C_2,…,C_k\}$ ，定义：

avg(C)=\frac{2}{|C|(|C|-1)} \sum_{1\le i\le j\le |C|}dist(x_i,x_j)\\ diam(C)=\max_{1\le i\le j\le |C|}dist(x_i,x_j)\\ d_{min}(C_i,C_j)=\min_{x_i\in C_i,x_j\in C_j}dist(x_i,x_j)\\ d_{cen}(C_i,C_j)=dist(\mu_i,\mu_j)

其中， $dist$ 表示两个样本之间的距离， $\mu$ 表示簇的中心点 $\mu=\frac{1}{|C|}\sum_{1\le i\le |C|}x_i$ 。 $avg(C)$ 表示簇 $C$ 内样本间的平均距离， $diam(C)$ 表示簇 $C$ 内样本的最远距离， $d_{min}$ 表示两个簇之间最近样本间的距离， $d_{cen}$ 表示两个簇的中心点之间的距离。

基于上述四个式子，可以推导出常用的聚类性能度量内部指标：

DB指数
$DBI=\frac{1}{k}\sum_{i=1}^k\max_{j\neq i}(\frac{avg(C_i)+avg(C_j)}{d_{cen}(C_i,C_j)})$
Dunn指数
$DI=\min_{1\le i\le k}\{\min_{j \neq i}(\frac{d_{min}(C_i,C_j)}{\max_{1\le l\le k}diam(C_l)})\}$

DBI的值越小越好，而DI的值越大越好。

3 距离计算

对于函数 $dist(\cdot,\cdot)$ ，若其是一个距离度量，则需要满足一些基本性质：

非负性： $dist(x_i,x_j)\ge 0$
同一性： $dist(x_i,x_j)=0$ 当且仅当 $x_i=x_j$
对称性： $dist(x_i,x_j)=dist(x_j,x_i)$
直递性： $dist(x_i,x_j)\le dist(x_i,x_k)+dist(x_k,x_j)$ ，可以理解成”三角不等式“

对于有序属性（例如{1，2，3}中1和2更接近，可以比较顺序，因此是有序属性；但是{飞机，火车，轮船}就很难找到顺序关系，因此不是有序属性），对于给定样本 $x_i=\{x_{i1},x_{i2},…,x_{in}\}$ 和 $x_j=\{x_{j1},x_{j2},…,x_{jn}\}$ ，最常用的距离函数是”闵可夫斯基距离“：

dist_{mk}(x_i,x_j)=(\sum_{u=1}^n |x_{iu}-x_{ju}|^p)^{\frac{1}{p}}

当 $p=1$ 时，该距离为曼哈顿距离
当 $p=2$ 时，该距离为欧氏距离

对于无序属性，我们可以采用 $VDM$ 来衡量距离。令 $m_{u,a}$ 表示属性 $u$ 上取值为 $a$ 的样本数， $m_{u,a,i}$ 表示第 $i$ 个样本簇中在属性 $u$ 上取值为 $a$ 的样本数， $k$ 为样本簇数，则属性 $u$ 上两个离散值 $a$ 与 $b$ 之间的 $VDM$ 距离为：

VDM_p(a,b)=\sum_{i=1}^k |\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}|

将闵可夫斯基距离和VDM距离结合起来即可处理混合属性，假定有 $n_c$ 个有序属性、 $n-n_c$ 个无序属性，且有序属性排列在无序属性之前：

MinkovDM_p(x_i,x_j)=(\sum_{u=1}^{n_c}|x_{iu}-x_{ju}|^p+\sum_{u=n_c+1}^nVDM_p(x_{iu},x_{ju}))^{\frac{1}{p}}

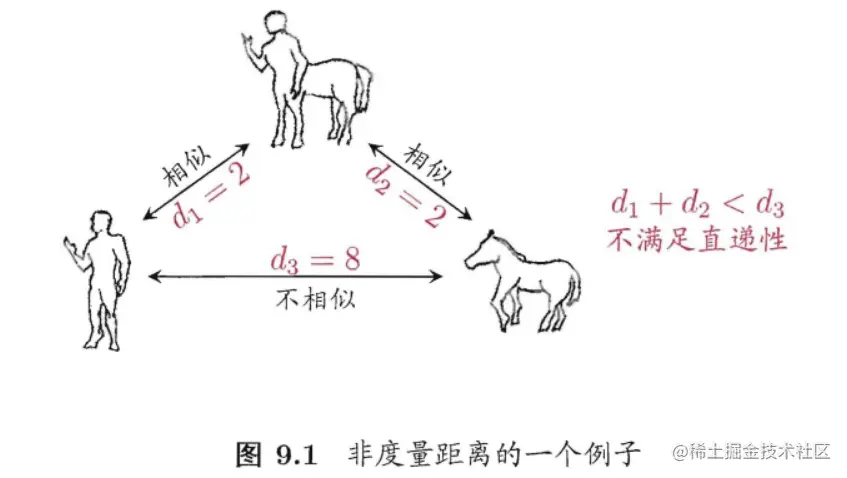
需注意的是，通常我们是基于某种形式的距离来定义“相似度度量”(similarity measure),距离越大，相似度越小。然而，用于相似度度量的距离未必一定要满足距离度量的所有基本性质，尤其是直递性。例如在某些任务中我们可能希望有这样的相似度度量:“人”、“马”分别与“人马”相似，但“人”与“马”很不相似；要达到这个目的,可以令“人”、“马”与”人马”之间的距离都比较小，但“人”与“马”之间的距离很大，如图所示，此时该距离不再满足直递性；这样的距离称为“非度量距离”(non-metric distance)。此外，本节介绍的距离计算式都是事先定义好的，但在不少现实任务中，有必要基于数据样本来确定合适的距离计算式，这可通过“距离度量学习”(distance metric learning)来实现。

4 原型聚类

原型聚类（prototype-based clustering）：假设聚类结构能通过一组原型刻画。通常情形下，算法对原型进行初始化，然后对原型进行迭代更新求解。

4.1 k均值算法

给定样本集 $D=\{x_1,x_2,…,x_m \}$ ，k均值（k-means）算法针对聚类所得簇划分 $C=\{C_1,C_2,…,C_k \}$ ，目标是最小化平方误差：

E=\sum_{i=1}^k \sum_{x\in C_i}||x-\mu_i||_2^2

其中 $\mu_i=\frac{1}{|C_i|}\sum_{x\in C_i}x$ 是簇 $C_i$ 的均值向量。直观来看，该式子刻画了簇内样本围绕簇均值向量的紧密程度， $E$ 值越小则簇内样本相似度越高。

k-means算法流程如下：

为了避免运行时间过长，通常会设置一个最大运行轮数或最小调整幅度阈值。

4.2 学习向量量化

学习向量量化（Learning Vector Quantization，检查LVQ）是试图找到一组原型向量来刻画聚类结构，但与一般聚类算法不同的是，LVQ假设数据样本带有类别标记，学习过程中用样本的监督信息来辅助聚类。

假定数据集 $D=\{(x_1,y_1),(x_2,y_2),…,(x_m,y_m) \}$ ，其中每个样本 $x_i$ 有 $n$ 个属性 $(x_{i1};x_{i2};…;x_{in})$ ， $y_i$ 是样本 $x_i$ 的类别标记。LVQ算法的目标是学习到一组 $n$ 维原型向量 $\{p_1,p_2,…,p_n\}$ ，每个原型向量代表一个聚类簇，簇标记 $t_i\in Y$ 。

LVQ算法描述如下：

通过该流程图，我们可以看出LVQ算法的关键在于上图中的6-10行，即原型向量的更新。直观上看，若样本 $x_j$ 的类别与原型向量 $p_i$ 相同，则令 $p_i*$ 向 $x_j$ 的方向靠拢：

p'=p_i*+\eta (x_j-p_i*)

$p'$ 与 $x_j$ 之间的距离为：

||p'-x_j||_2 =||p_i*+\eta(x_j-p_i*)-x_j||_2 =(1-\eta)\cdot||p_i* -x_j||_2

其中， $\eta$ 是学习率，位于 $(0,1)$ 之间。类似地，如果样本 $x_j$ 的类别与原型向量 $p_i$ 不同，则将距离增大为 $(1+\eta)||p_i*-x_j||_2$ ，令原型向量和 $x_j$ 的距离增大。

通过上述过程，对任意的样本 $x_j$ ，它将被划入到与其距离最近的原型向量所代表的簇中；换言之，每个原型向量 $p_i$ 定义了与之相关的一个区域 $R_i$ ，该区域中每个样本与 $p_i$ 的距离不大于它与其他原型向量的距离，即

R_i=\{x\in X|\space||x-p_i||_2 \le||x-p_{i'}||_2,i\neq i' \}

由此形成了对样本空间 $X$ 的簇划分 $\{R_1,R_2,…,R_q\}$ ，通常该划分称为“Voronoi剖分”。

4.3 高斯混合聚类

高斯混合聚类（Mixture-of-Gaussian）采用概率模型来表达聚类原型。

高斯分布的概率密度函数如下：

p(x)=\frac{1}{(2\pi)^{\frac{n}{2}}|\sum|^{\frac{1}{2}}} e^{-\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu)}

其中， $\mu$ 是 $n$ 维均值向量， $\sum$ 是 $n \times n$ 的协方差矩阵（对称正定矩阵）。

为了明确显示高斯分布与相应参数的依赖关系，我们将概率密度函数记为 $p(x|\mu,\sum)$ ，定义高斯混合分布，其中 $\alpha_i$ 为混合系数（mixture coefficient），：

p_M(x)=\sum_{i=1}^k \alpha_i\cdot p(x|\mu_i,\sum_i)\\ \sum_{i=1}^k \alpha_i=1

假设样本的生成过程由高斯混合分布给出，根据 $\alpha_i$ 定义的先验分布选择高斯混合分布（ $\alpha_i$ 表示选择第 $i$ 个分布的概率），然后根据被选择的混合成分的概率密度函数进行采样，从而生成相应的样本。

若训练集 $\{x_1,x_2,…,x_m\}$ 由上述过程给出，令随机变量 $z_j\in {1,2,…,k}$ 表示生成样本 $x_j$ 的高斯混合成分，其取值未知。显然 $z_j$ 的先验概率 $P(z_j=i)$ 对应于 $\alpha_i$ 。其后验概率对应于下式，并记为 $\gamma_{ji}$ ：

p_M(z_j=i|x_j)=\frac{P(z_j=i)\cdot p_M(x_j|z_j=i)}{p_M(x_j)} =\frac{\alpha_i\cdot p(x_j|\mu_i,\sum_i)}{\sum_{l=1}^k \alpha_l\cdot p(x_j|\mu_l,\sum_l)}

当混合高斯分布已知时，高斯混合聚类将样本集划分为 $k$ 个簇，每个样本 $x_j$ 的簇标记 $\lambda_j$ 如下确定（即高斯混合聚类采用概率模型对圆形进行刻画，簇划分由原型对应的后验概率确定）：

\lambda_j=\mathop{\arg \max}_{i\in \{1,2,…,k\}} \gamma_{ji}

由最大化对数似然和EM算法，我们可以求解 $\alpha_i$ ：

\alpha_i=\frac{1}{m}\sum_{j=1}^m\gamma_{ji}

即每个高斯分布的混合系数由样本属于改成份的平均后验概率确定。

高斯混合聚类的流程如下：

5 密度聚类

密度聚类（density-based clustering）：假设聚类结构能通过样本的分布的紧密程度决定。通常情况下，密度聚类算法从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。

DBSCAN是一种著名的密度聚类算法，其基于一组“邻域”（neighborhood）参数（ $\epsilon,MinPts$ ）来刻画样本分布的紧密程度。给定数据集 $D=\{x_1,x_2,…,x_m\}$ ，定义以下几个概念：

$\epsilon-$ 邻域：对于 $x _j\in D$ ，其 $\epsilon-$ 邻域包含样本集 $D$ 中与 $x_j$ 的距离不大于 $\epsilon$ 的样本，即
$N_\epsilon(x_j)=\{x_j\in D|dist(x_i,x_j)\le \epsilon \}$
核心对象（core object）：若 $x_j$ 的 $\epsilon-$ 邻域至少包含 $MinPts$ 个样本，即 $|N_\epsilon(x_j)|\ge MinPts$ ，则 $x_j$ 是一个核心对象。
密度直达（directly density-reachable）：若 $x_j$ 位与 $x_i$ 的 $\epsilon-$ 邻域内，且 $x_i$ 是核心对象，则称 $x_i$ 和 $x_j$ 密度直达。
密度可达（density-reachable）：对 $x_i$ 和 $x_j$ ，存在样本序列 $p_1,p_2,…,p_n$ ，其中 $p_1=x_i,p_n=x_j$ ，且 $p_{i+1}$ 和 $p_i$ 密度直达，则称 $x_i$ 和 $x_j$ 密度可达。
密度相连（density-connected）：对 $x_i$ 和 $x_j$ ，若在 $x_k$ 使得 $x_i$ 与 $x_j$ 均由 $x_k$ 密度可达，则称 $x_i$ 与 $x_j$ 密度相连。

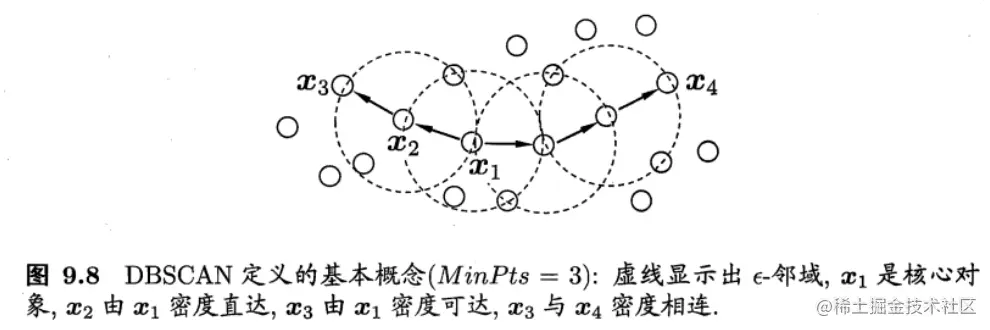
基于上述概念，DBSCAN将“簇”定义为：由密度可达关系导出的最大密度相连样本集合。形式化的说就是，给定邻域参数（ $\epsilon,MinPts$ ）,簇 $C \subseteq D$ 是满足以下性质的非空样本子集：

连接性： $x_i \in C$ ， $x_j\in C \Rightarrow x_i$ 和 $x_j$ 密度相连
最大性： $x_i \in C, x_j$ 可由 $x_i$ 密度可达 $\Rightarrow x_j\in C$

若 $x$ 是核心对象，由 $x$ 密度可达的所有样本组成的集合记为 $X = \{x' \in D|x'由x密度可达 \}$ 是满足最大型和连接性的簇。

DBSCAN算法先任选数据集中一个核心对象为种子（seed），再由此出发确定相应的聚类簇。算法描述如下：

6 层次聚类

层次聚类（hierarchical clustering）试图在不同层次对数据集进行划分，从而形成树形的聚类结构。数据集的划分可以采用 “自底向上”的聚合策略，也可采用 “自顶向下”的分拆策略。

AGNES是一种采用自底向上聚合策略的层次聚类算法。它先将数据集的每个样本看作一个初始聚类簇，然后再算法运行的每一步中找出距离最近的两个聚类簇进行合并，该过程不断重复，直至达到预设的聚类簇个数。

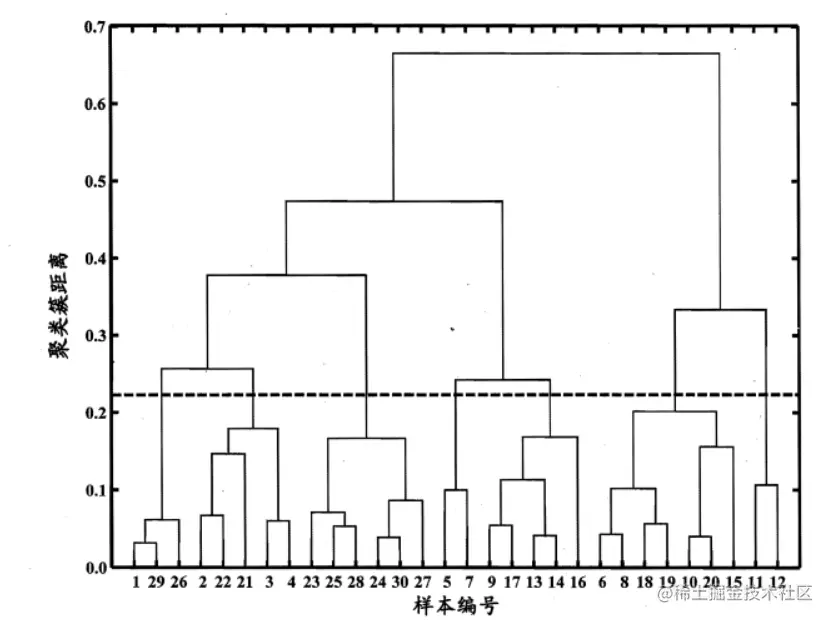
给定聚类簇 $C_i$ 和 $C_j$ ，其距离公式如下：

单链接：最小距离 $d_{min}(C_i,C_j)=\min_{x\in C_i,z\in C_j} dist(x,z)$
全链接：最大距离 $d_{max}(C_i,C_j)=\max_{x\in C_i,z\in C_j} dist(x,z)$
均链接：平均距离 $d_{avg}(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum_{x\in C_i}\sum_{z\in C_j} dist(x,z)$

机器学习 第九章聚类