Multi-Modal Distance Metric Learning

简介

随着社交媒体的快速发展，多模态数据正在急剧增加，本文提出了一种有效的、可扩展的多模态距离度量学习框架。该方法基于multi-wing harmonium 模型，提供了一种原则性的方法，可以将任意形态的数据嵌入到一个单一的潜在空间中，在适当的监督下，可以得到一个最优的距离矩阵，即最优距离矩阵（即最小化相似对之间的距离，最大化不相似对间的距离）。

Multi-Modal Distance Metric Learning

Multi-Wing Harmonium 模型

dual-wing harmonium 模型（DWH）如图1所示，它由两种输入单元模态组成： $X=\{x_i\},Z=\{z_j\}$ ， $H=\{h_k\}$ 为一组隐藏单元。在这种无向图模型中，两种输入模式之间不存在联系。每个输入单元的模态和隐藏单元形成一个完全二分图，其中同一组中的单元没有连接，而另一组中单元完全连接。

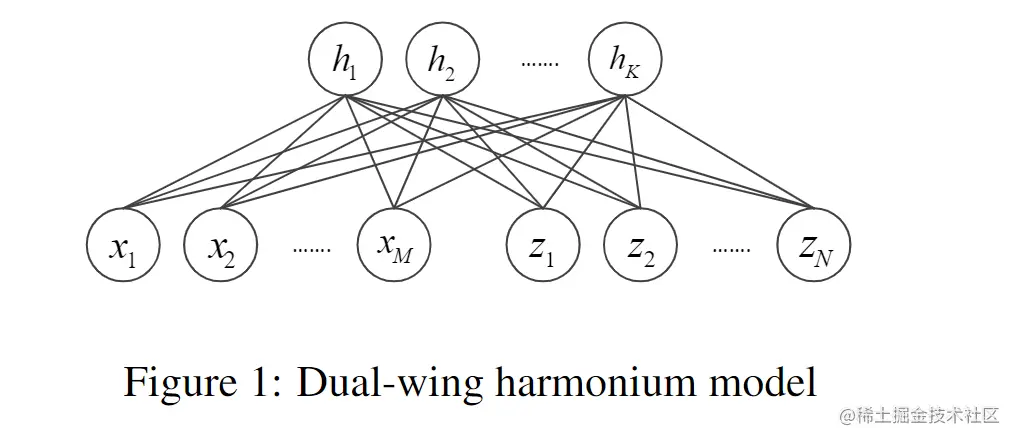
这种拓扑结构引出了3个条件独立假设：

给定潜在变量 $H$ 时，两个模态 $X,Z$ 是相互独立的： $p(X,Z|H)=p(X|H)p(Z|H)$
给定 $X,Z$ 时， $H$ 中的每个单元是互相独立的： $p(K|X,Z)=\prod_kp(h_k|X,Z)$
给定 $H$ ，每种模态的单位都是独立的： $p(X|H)=\prod_i p(x_i|H),p(Z|H)=\prod_j(z_j|H)$

考虑所有观察到的和隐藏的变量都来自于指数族（exponential family）的情况，可以得到：

p(x_i)=e^{\theta^T_i\phi(x_i)-A(\theta_i)},p(z_j)=e^{\eta^T_j\varphi(z_j)-B(\eta_j)},p(h_K)=e^{\lambda^T_k\psi(h_k)-C(\lambda_k)}

$\theta_i,\eta_j,\lambda_k$ 为自然参数， $\phi(),\varphi(),\psi()$ 为充分统计量， $A(),B(),C()$ 为对数配分函数。（关于指数族分布的基础知识）

通过引入一个附件项耦合对数域上的随机变量，得到联合分布形式：

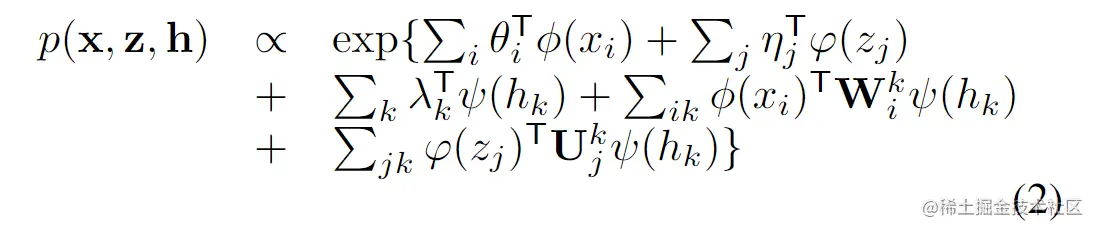
使用 $\Theta$ 来表示所有的参数 $(\theta,\eta,\lambda,W,U)$ 。根据联合分布得到条件分布：

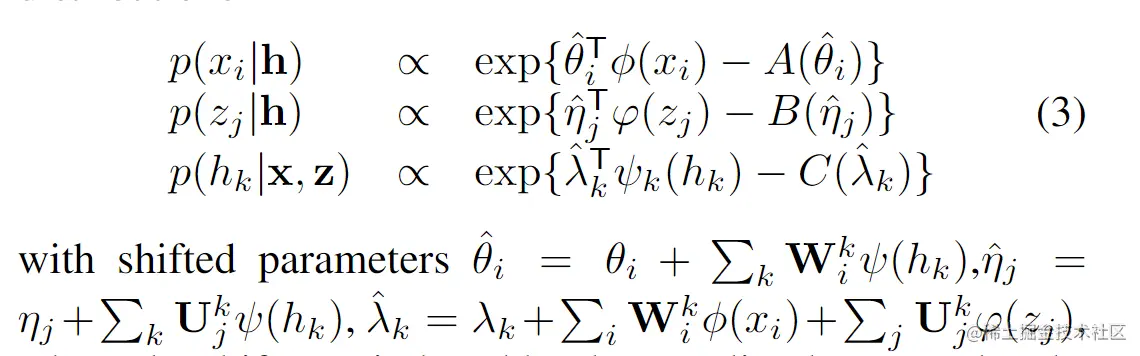
此处的shifts是基于观察到的和隐藏单元间的耦合关系确定。

根据具体的应用可以首先指定公式（3）中的本地条件分布，然后还计算公式（2）中的联合分布，这就是所谓的自下而上的dual-wing harmonium 模型，这个模型也很容易可以扩展成multi-wing harmonium （MWH）。

Multi-Modal Distance Metric Learning

本节中，介绍如何使用 MWH 模型来学习多模态距离测量。给定数据点 $y=(x,z)$ 有两种模态 $x,z$ 。在DWH框架中，可以将 $y$ 嵌入到公共潜在空间中，并得到其潜在表示 $t$ ：

t=\mathbb{E}_{p(h|x,z;\Theta)}[H]

显然 $t$ 是一个关于 $\Theta$ 的函数， $\mathbb{E}$ 表示数学期望。从语义上介绍，演出单元 $H$ 可以看做是一组隐藏主题，而不同源的观察值反映的是来自不同专题的中心主题，并由共享主题生成。

给定一组标记为相似或不相似的数据对，在潜在空间中强制相似对彼此接近，而不同对彼此远离。文章简单的使用欧氏距离作为距离度量来度量潜在空间中的嵌入点。令 $S=\{y^{(i)},y^{(j)}\}$ 表示相似数据对， $D=\{y^{(i)},y^{(j)}\}$ 表示不相似数据对。得到下面的优化问题：

\min_{\Theta}\sum_{(y^{(i)},y^{(j)})\in S}||t^{(i)}-t^{(j)}||^2 \\ \ \\ s.t.\ \forall (y^{(i)},y^{(j)})\in D,||t^{(i)}-t^{(j)}||^2 \geq 1

$t^{(i)}$ 为 $y^{(i)}$ 的潜在空间，该函数的目标是在保持不相似点间在潜在空间的距离为1的情况下尽可能减小相似点间的距离，需要学习的参数是 $\Theta$ 。

用 $Y$ 表示 $S$ 或 $D$ 中的所有数据示例，无监督DWH模型通过最大化数据观察 $Y$ 的似然值来学习参数 $\Theta$ 。有监督DWH模型结合距离度量学习和最大似然学习通过联合最大函数似然值来学习 $\Theta$ 。具体的，将优化问题定义为：

\min_{\Theta} \frac{1}{|Y|}L(Y;\Theta)+\lambda\frac{1}{|S|}\sum_{(y^{(i)},y^{(j)})\in S}||t^{(i)}-t^{(j)}||^2 \\ \ \\ s.t.\ \forall (y^{(i)},y^{(j)})\in D,||t^{(i)}-t^{(j)}||^2 \geq 1 \tag{6}

$L(Y;\Theta)$ 是一个关于数据 $Y$ 的负对数似然， $\lambda$ 为权衡参数。

优化

本节提出了公式（6）的一个有效解法，使用hinge loss来消除公式（6）中的约束，得到：

\min_{\Theta} \frac{1}{|Y|}L(Y;\Theta)+\lambda_1\frac{1}{|S|}\sum_{(y^{(i)},y^{(j)})\in S}||t^{(i)}-t^{(j)}||^2+\lambda_2\frac{1}{|D|}\sum_{(y^{(i)},y^{(j)})\in D}\max(0,1-||t^{(i)}-t^{(j)}||^2) \\ \ \\ \tag{7}

公式（7）为公式（6）的松弛版本，当公式（6）中的约束满足要求时，公式（7）中的hinge loss为0。不满足要求是， hinge loss不为0，并最小化强制满足约束。

使用contrastive divergence方法来近似 $\Theta$ 关于 $\frac{1}{|Y|}L(Y;\Theta)$ （负对数似然）的梯度，总之，参数的次梯度与方程(7)中定义的目标函数可以计算如下：

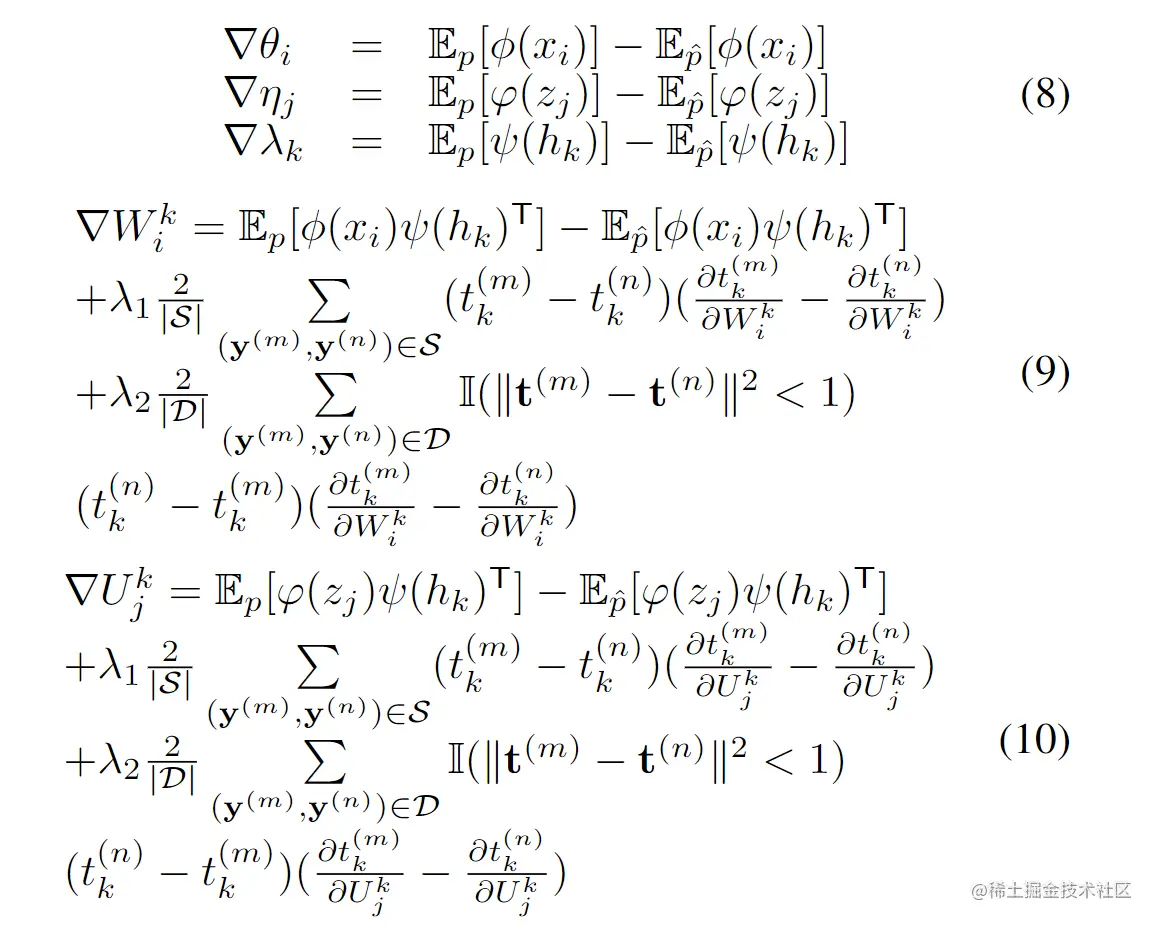
其中 $\mathbb{E}_p[]$ 表示真实分布的期望， $\mathbb{E}_{\hat{p}}[]$ 表示经验分布的期望。精确计算 $\mathbb{E}_p[]$ 是非常困难的，因此通过从 $\mathbb{E}_{\hat{p}}[]$ 中运行一些Gibbs 采样来估算 $\mathbb{E}_p[]$ ，采样可以按以下方式迭代完成：

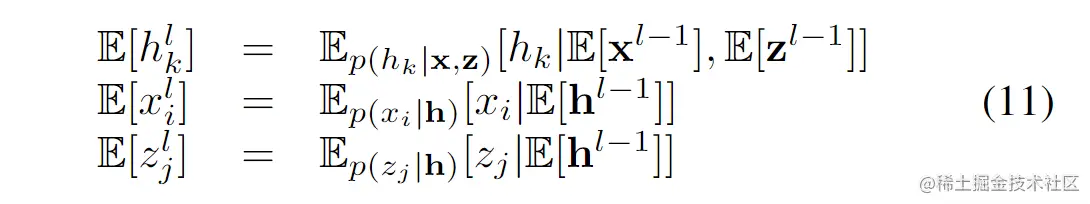
$l$ 为迭代的索引号。