这是我参与2022首次更文挑战的第29天,活动详情查看:2022首次更文挑战
之前我们提到在Sequence to sequence模型中选择最有可能性的输出的时候,不能使用贪心算法。
我们还说过学过算法的都知道,贪心算法可以较快的得到结果,但是它的结果可能并不是全局最好的;穷举算法可以达到最好的结果,但是它的计算量往往过于巨大。在这个基础上我们可以使用一种折中的算法,就是启发式的搜索算法——束搜索(Beam Search)。
举个例子
还是使用这个例子:
一句法语Jane visite l’Afrique en septembre.将其翻译为英语。
step 1
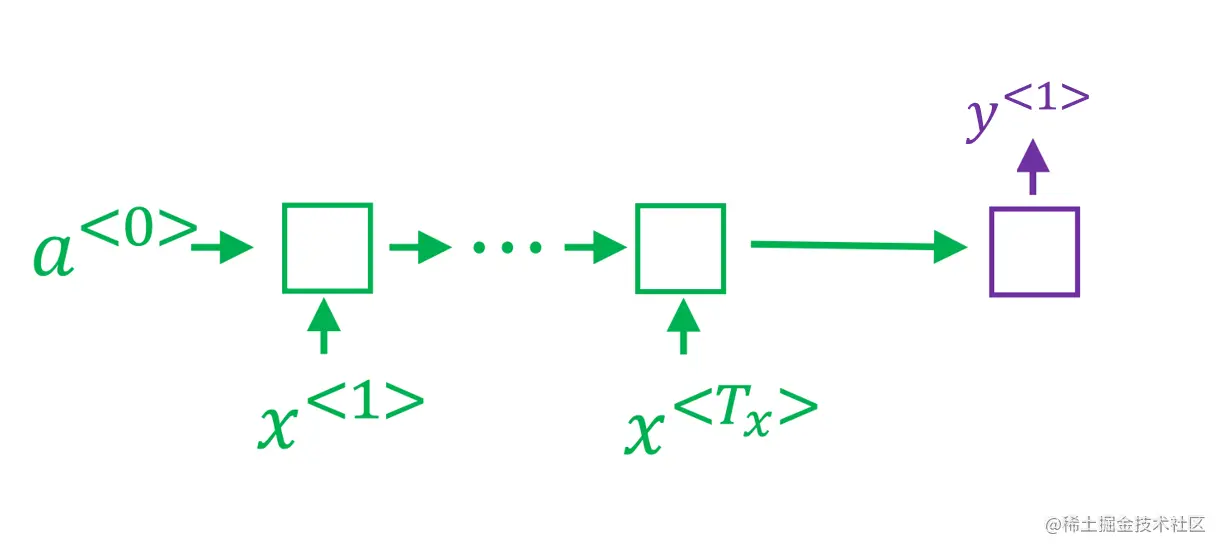
第一步我们是要计算:
P(y<1>∣x)
和贪心算法不太一样的地方在于贪心算法需要找到一个最优值,束搜索需要设置一个搜索宽度K,在这里我们设置K=3。之后就会选择出三个最有可能的词语作为候选。然后进入第二步。

贪心算法只找最佳候选,穷举是所有候选都考虑,束搜索是只考虑K个候选。
setp 2
第二步我们是要计算:
P(y(2)∣x,y(1))
这一步我们需要在前三种情况的基础上再进行搜索,再找出三个最可能的结果。这里是在前三种搜索的基础上,再筛选出来三种;不是说在前三种的基础上,每种再筛选出来三种。是3万里边选3个,不是3万里边选9个。

-
在第一步第一个候选“in”的基础上进行计算。
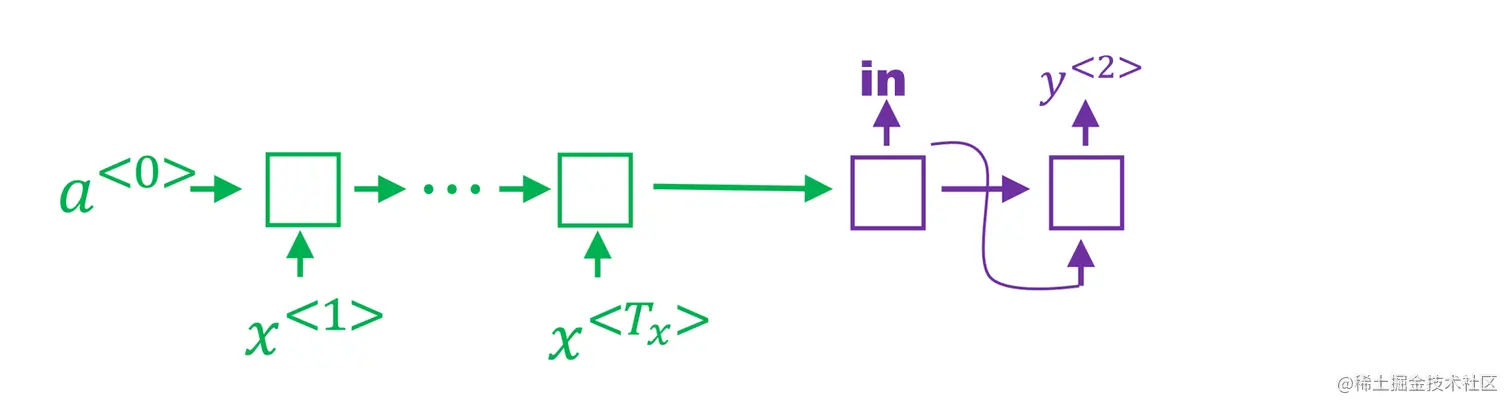
P(y(2)∣x,′in′)
-
在第一步第二个候选“jane”上进行计算。
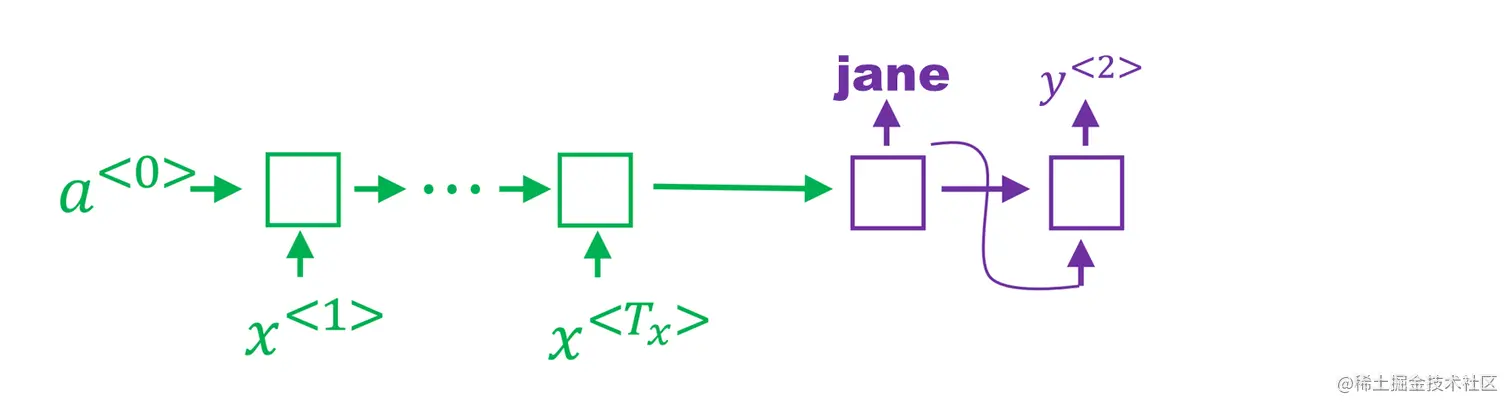
P(y(2)∣x,′jane′)
-
在第一步第三个候选“september”基础上进行计算。
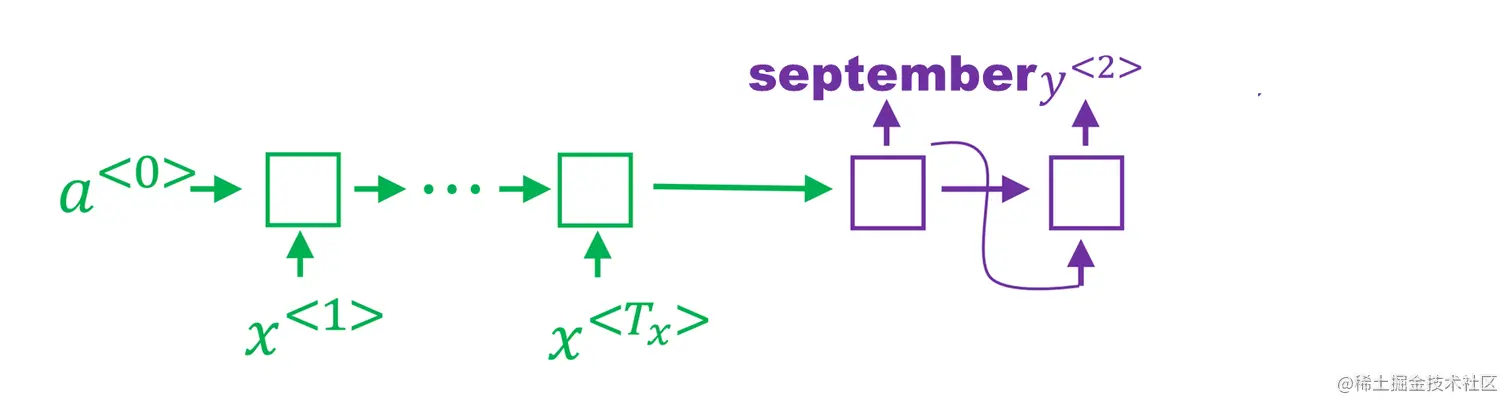
P(y(2)∣x,′september′)
step 3
第三步就是要计算:
P(y(3)∣x,y(1),y(2))
第一二步看完以后应该就已经弄懂原理了,第三步我们就快速的说一下。依旧是在前两个节点的基础上。进行最优的三个选择。还是选出来三个。之后的第四步第五步,以此类推一直到句子的末尾eos。
-
在前两步是“in september”的基础上进行计算。
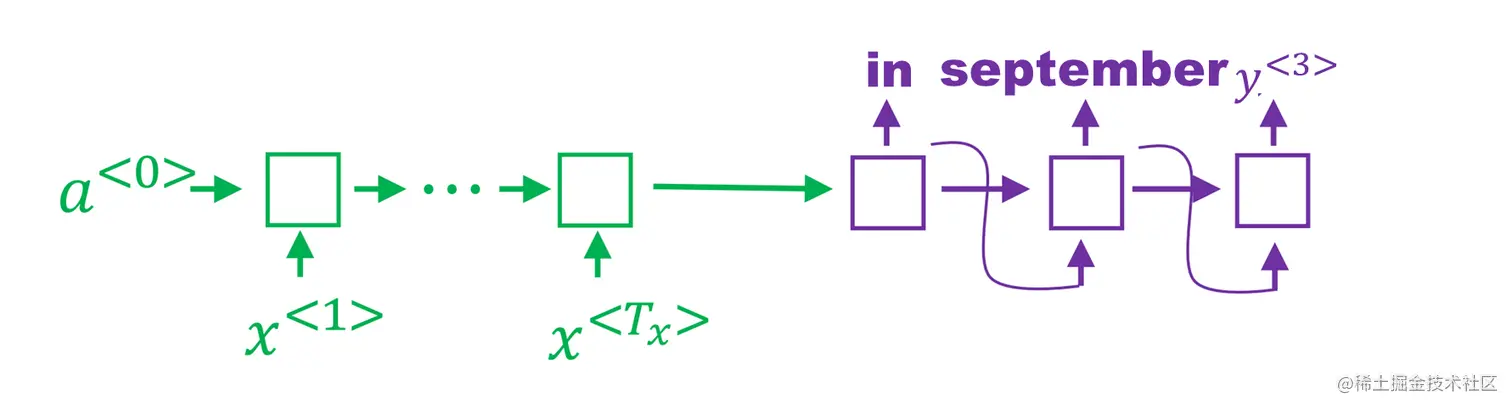
P(y(3)∣x,′inseptember′)
-
在前两步是“jane is”的基础上进行计算。
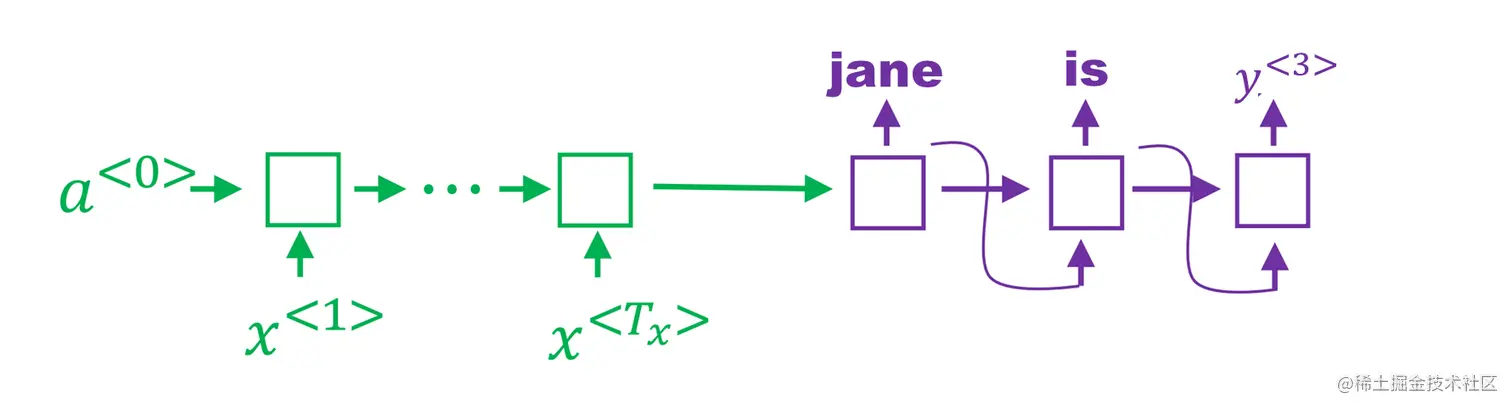
P(y(3)∣x,′janeis′)
-
在前两步是“jane visit”的基础上进行计算。
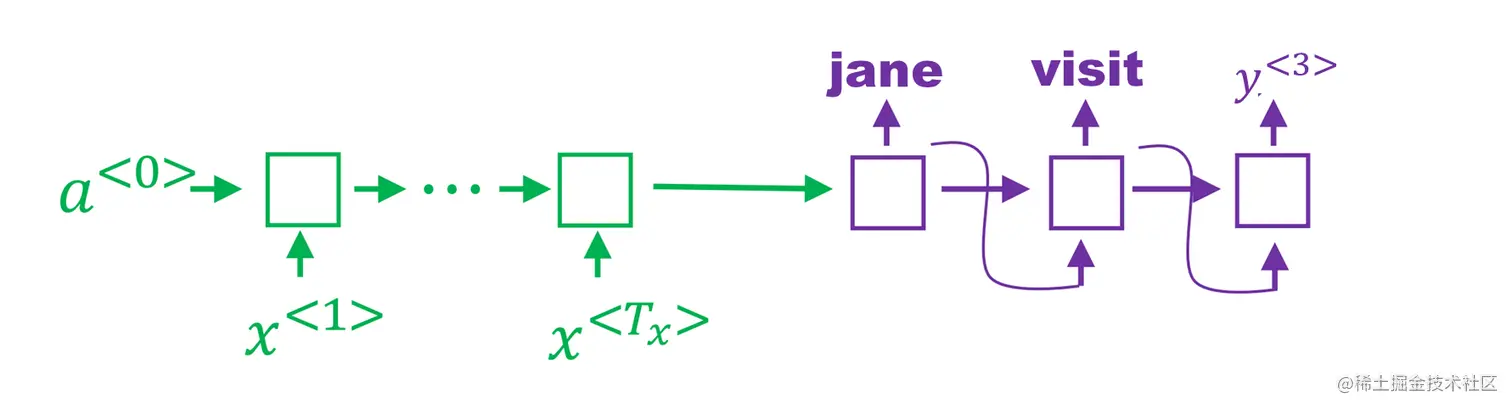
P(y(3)∣x,′janevisit′)
总结
总之整个算法要做的事就是:
argymaxt=1∏TyP(y<t>∣x,y<1>,…,y<t−1>)
将这个概率进行最大化,以求取当前最佳的句子。
束搜索
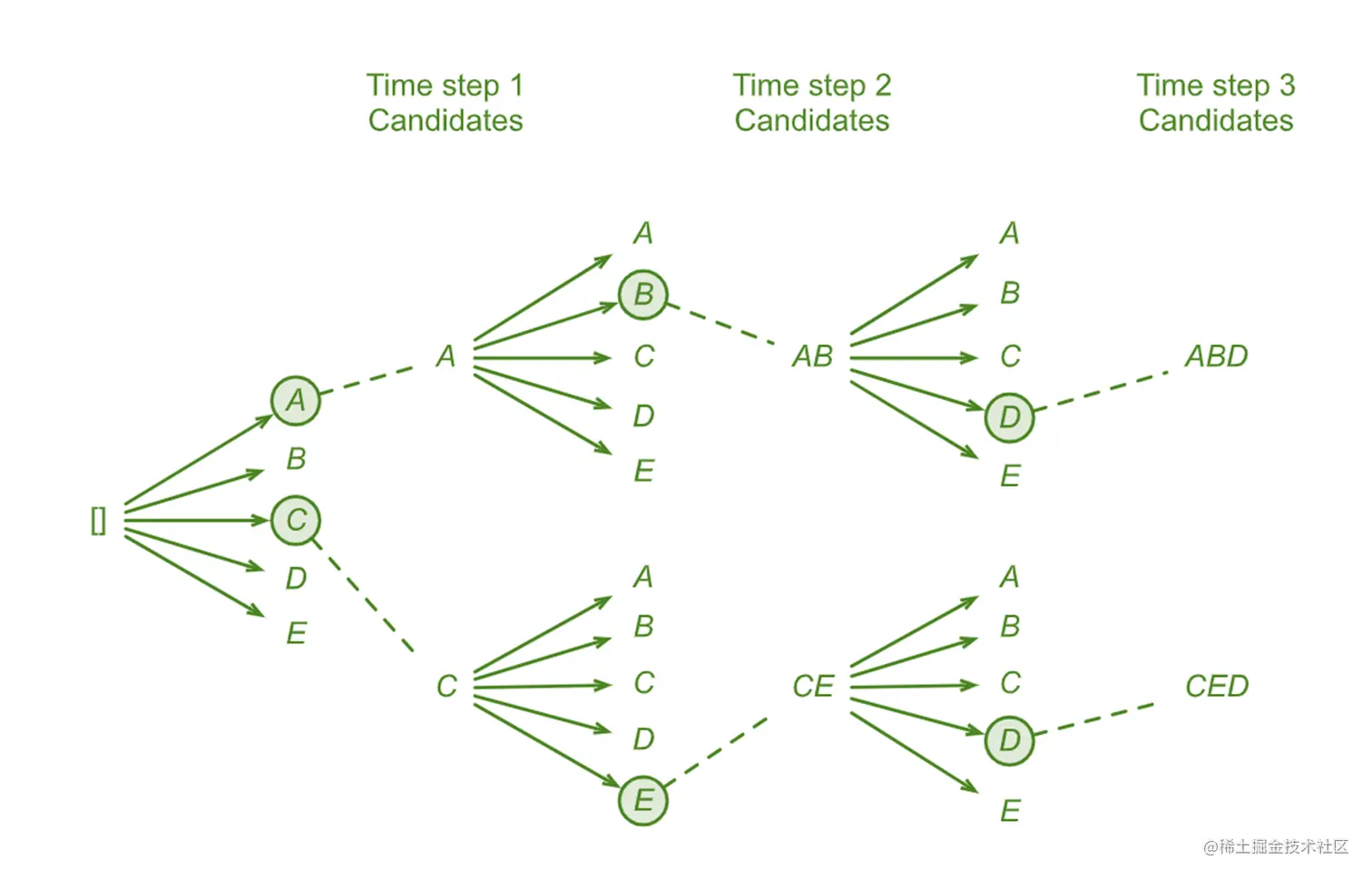
束搜索(beam search) 是贪心搜索的一个改进版本。它有一个超参数,名为束宽(beam size)。在时间步1,我们选择具有最高条件概率的k个词元。这k个词元将分别是k个候选输出序列的第一个词元。在随后的每个时间步,基于上一时间步的k个候选输出序列,我们将继续从k个可能的选择中挑出具有最高条件概率的k个候选输出序列。
值得注意的一点是当K等于1的时候,束搜索就会退化为贪心算法。
束搜索🔍现存问题
束搜索要做的其实就是:
argymaxt=1∏TyP(y<t>∣x,y<1>,…,y<t−1>)
其中
p(y(1)…y(Ty)∣(x))=p(y(1)∣x)×p(y(2)∣x,y(1))×...×p(y(Ty)∣x,y(1)…,y(Ty−1))
这个计算公式在实际的计算过程中会产生两个问题。
- 计算下溢:首先在实际的计算过程当中,因为这些概率都是一个小于1的值。当多个小于1的值进行相乘的时候,很可能会出现数据下溢的情况。
- 判断失误:因为我们要求的是argmaxy∏t=1TyP(y<t>∣x,y<1>,…,y<t−1>),也就是说要对这个公式进行最大化计算。所以会造成一个问题,就是他会倾向于更短的句子。因为同样都是小于一的数字相乘,乘出来的数字会越来越小。0.1×0.1×0.1×0.1×0.1和0.1×0.1×0.1×0.1×0.1×0.1×0.1×0.1×0.1哪个更小一目了然。当然实际过程中并不是每个概率都是0.1。但是短的句子总会取得较大的计算值这个是毋庸置疑的。所以输出通常会偏向于更短的句子。
解决计算下溢问题
解决计算下溢问题,我们通常是会进行一个取对数值计算。
argymaxy=1∑TylogP(y<t>∣x,y<1>,…,y<t−1>)
将原来的乘积变成了一个对数计算的求和。
取对数之后不会改变数据的性质和相关关系,但压缩了变量的尺度,所以计算这个式子跟计算原来的式子结果是一样的。并且在有些情况下,取对数可以消除异方差,从而达到平稳化的目的,取对数之后会获得一个数值上更加稳定的算法。不容易在计算机中出现数值舍如的误差,或者说数值的下溢。
但是我们会发现虽然这个解决了一个问题,但是另一个问题还是没有解决。从小数字相乘变成小数的相加。由于对数值的计算,小数越来越多的时候也会越来越趋向于负无穷。但是这个问题我们可以结合着输出倾向更短这个问题一起来解决。
解决输出倾向问题
句子长短而导致输出结果受影响,这个我们可以加上一,。来消除句子长短造成的差异,即对其进行归一化。
Ty1t=1∑TylogP(y<t>∣x,y<1>,…,y<t−1>)
除以句子长度对其进行归一化。
当然还有一种探索性的改进。
Tyα1t=1∑TylogP(y<t>∣x,y<1>,…,y<t−1>)
相比于直接除以句子的长度Ty,往往会采取一种更柔和的方式,就是为其添加上一个指数项α,为其设定不同的数值。