【从0上路图形学】视图变换与投影（Model View Transformation）games 101 第 4 课的笔

本文是games 101 Lecture 04的学习笔记，如果对二维空间中的变换不是很了解可以先浏览上一篇

三维空间中的变换

参照二维中的形式，三维空间中的仿射变换（Affine Transformation）都可以用如下 4 $\times$ 4 齐次坐标下的矩阵乘积表示，其中 $t_x,t_y,t_z$ 为在各个方向上平移的距离。

\begin{pmatrix} x^\prime \\ y^\prime \\ z^\prime \\ 1 \end{pmatrix} = \begin{pmatrix} a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}

\begin{pmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

首先来看较简单的绕 x，y，z 三个轴的旋转

\begin{pmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}

我们可以得到在三维空间中绕 x，y，z轴的旋转变化矩阵分别为

R_x(\theta) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\theta & -sin\theta & 0 \\ 0 & sin\theta & cos\theta & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

R_y(\theta) = \begin{pmatrix} cos\theta & 0 & sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -sin\theta & 0 & cos\theta & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

R_z(\theta) = \begin{pmatrix} cos\theta & -sin\theta & 0 & 0 \\ sin\theta & cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

而对于给定旋转轴的旋转公式，可以参考# Rodrigues' rotation formula

观测变换包含三个部分，这里可以用照相举例

首先，我们通过下面三个向量定义好相机的位置的方向

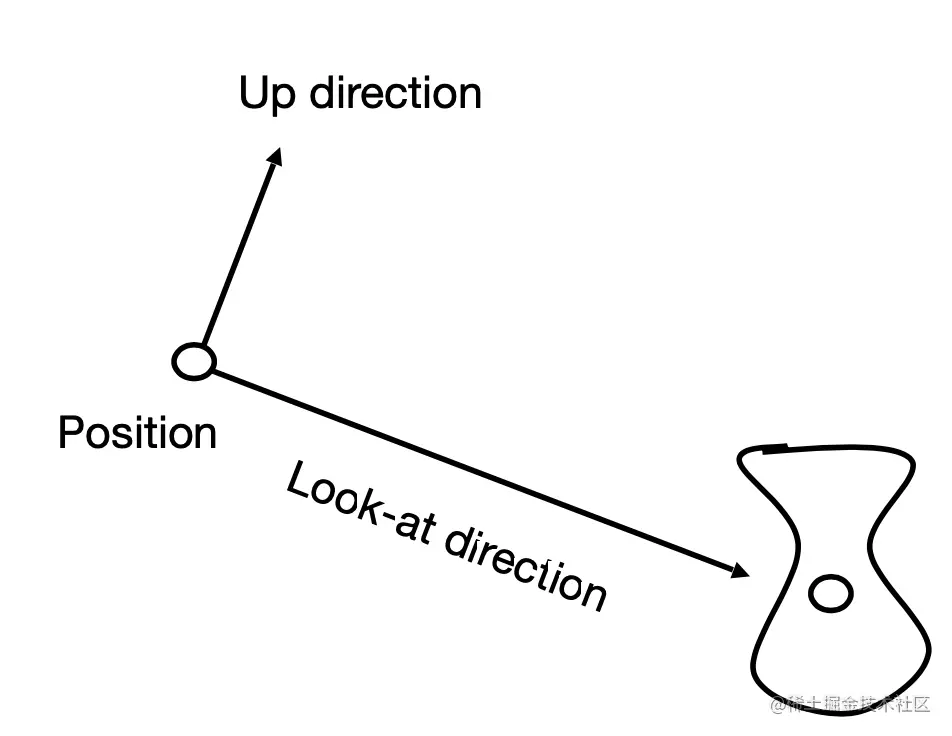
截屏2022-02-27 上午12.52.05.png

因为拍出来的照片取决于相机和被观测物体间的相对位置，所以为了方便我们作这样一个约定，相机永远位于原点，看向 -z 方向且向上朝着 y 方向，我们将相机的移动转化为被观测物体的相对运动。而实现这个转化的操作可以分为以下两步

T_{view} = \begin{pmatrix} 1 & 0 & 0 & -e_x \\ 0 & 1 & 0 & -e_y \\ 0 & 0 & 1 & -e_z \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

将 $\vec{g}$ 移到 $(0, 0, -1, 0)$ ， $\vec{t}$ 移到 $(0, 1, 0, 0)$ ，这一步的求解思路比较巧妙。我们可以先去构造这两个向量旋转到 $\vec{g}$ 和 $\vec{t}$ 的矩阵 $R_view^{-1}$ ，然后在来求它的逆。因为这是旋转变换，所以一定是个正交矩阵，而正交矩阵的逆就是它的转置矩阵。我们得到

R_{view} = \begin{pmatrix} {\vec{g}\times\vec{t}}_x & {\vec{g}\times\vec{t}}_y & {\vec{g}\times\vec{t}}_z & 0\\ t_x & t_y & t_z & 0 \\ -g_x & -g_y & -g_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

至此，我们已经推导出 Model 和 View Transformation 的公式了，当我们对场景中的物体和相机都运用下面的公式即可在保持相机物体相对位置不变的前提下，将相机移动到我们想要的位置了

M_{view} = R_{view}T_{view}

正交投影不会造成近大远小（道理我都懂，为什么鸽子这么大～）。

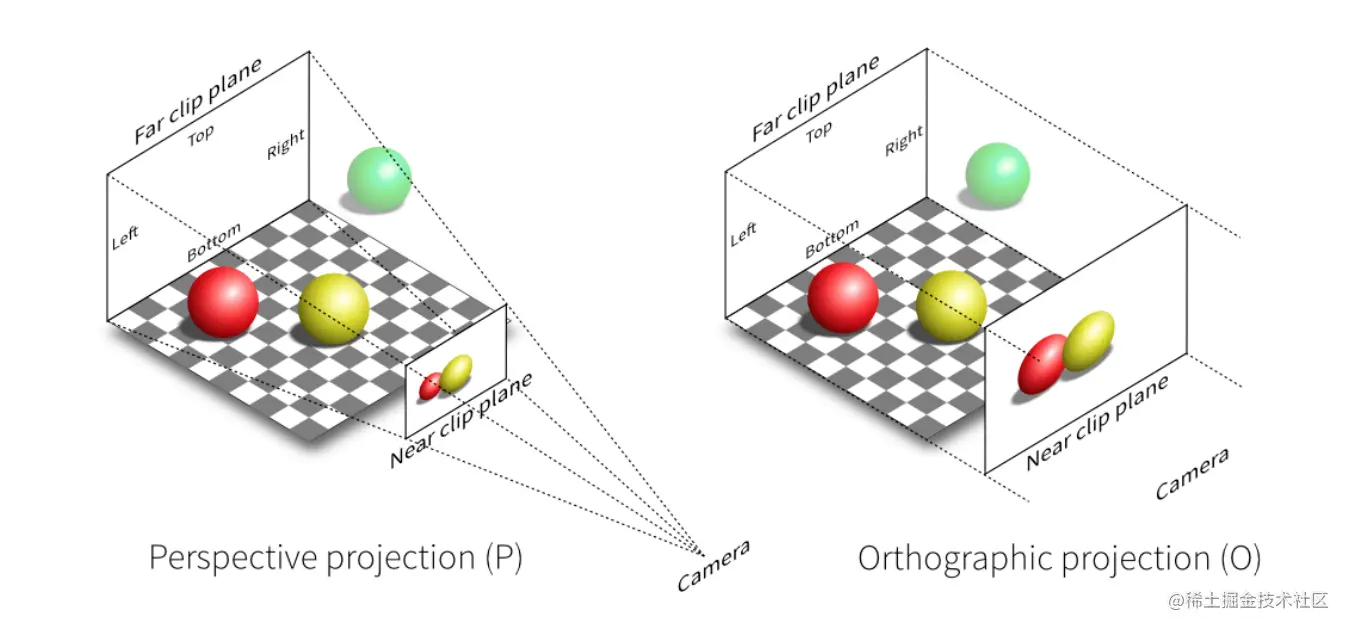截屏2022-02-27 上午10.45.07.png 正交投影可以理解为以下步骤

但在实际操作中，我们相当于把空间中的一个左右，上下，前后坐标分别为 $[l, r], [t, b], [f, n]$ 的立方体给映射到 $[-1, 1^3]$ 这么一个规范立方体中（canonical cube）。而这一步操作其实很简单，只需要先平移，再缩放即可。

M_{ortho} = \begin{pmatrix} \frac{2}{r - l} & 0 & 0 & 0 \\ 0 & \frac{2}{t - b} & 0 & 0 \\ 0 & 0 & \frac{2}{n - f} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & -\frac{2}{r + l} \\ 0 & 1 & 0 & -\frac{2}{t + b} \\ 0 & 0 & 1 & -\frac{2}{n + f} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

透视投影可以理解为这么两步，先将 Frustum 压缩到一个立方体内，然后再将立方体做一次正交投影。需要注意的是

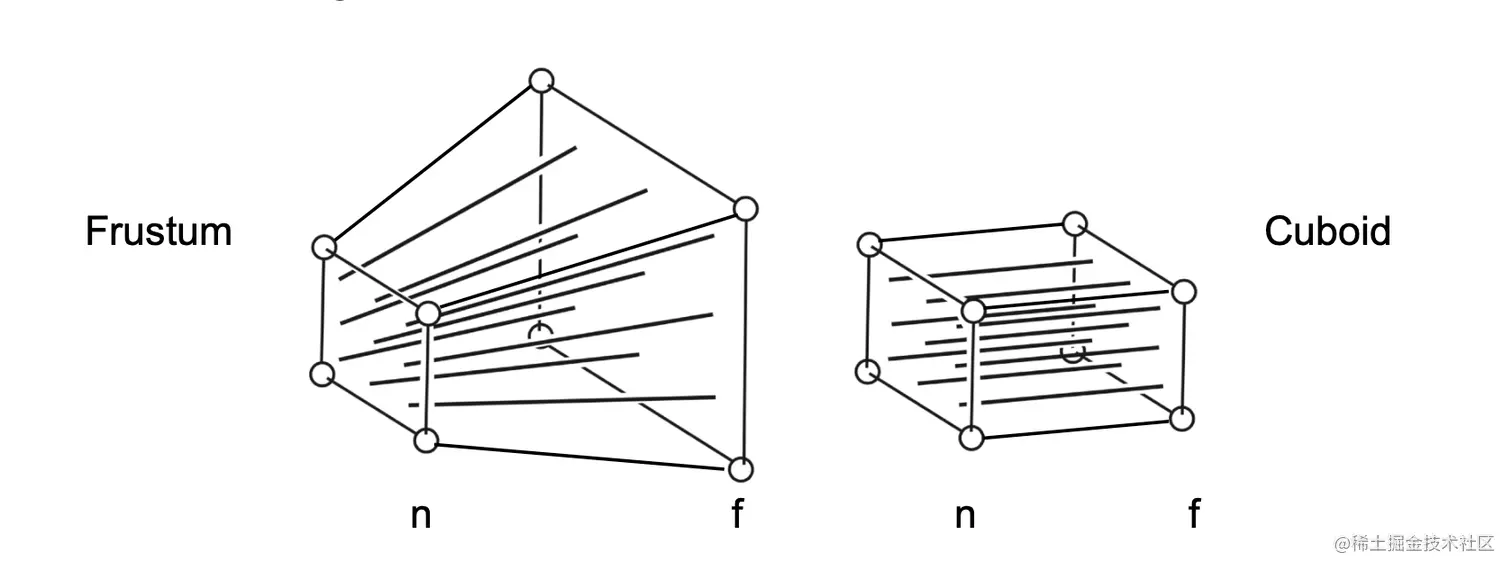
截屏2022-02-27 上午11.15.37.png

根据相似三角形的原理，我们可以得到任意一点在挤压后的 x，y 坐标与之前的关系

y^\prime = \frac{z}{n}y \space\space\space\space\space\space\space\space\space\space\space\space x^\prime = \frac{z}{n}x

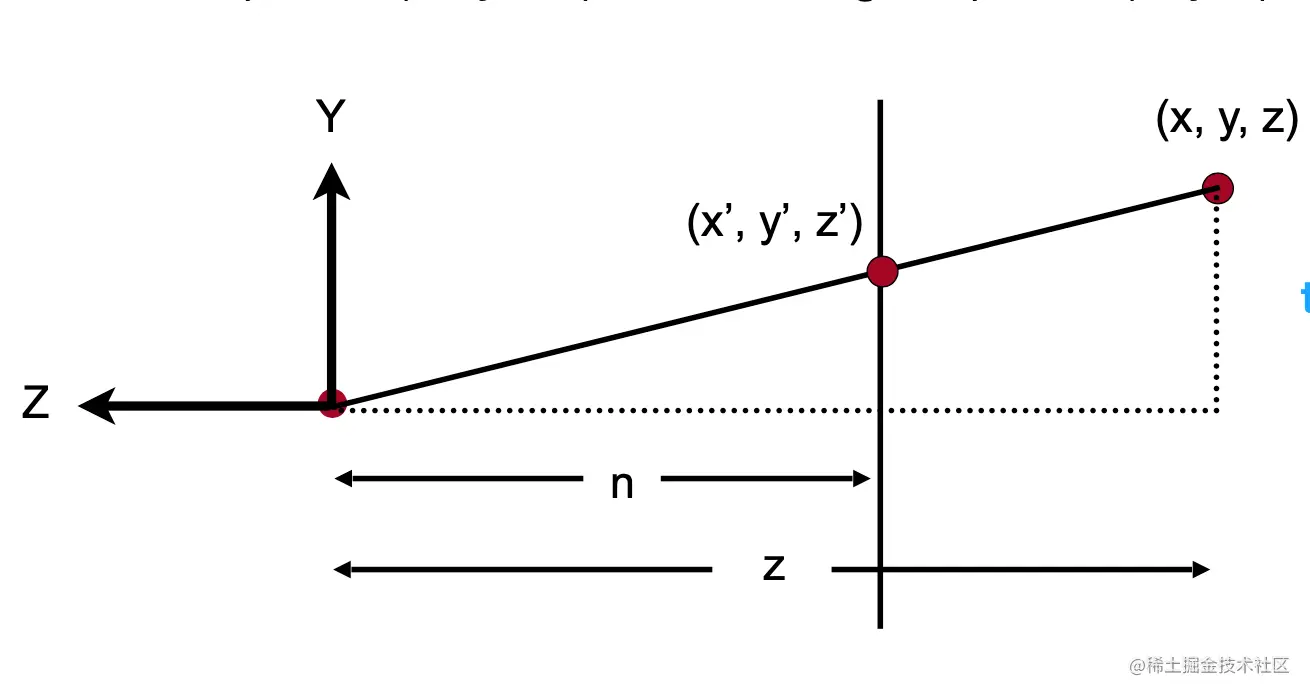截屏2022-02-27 上午11.25.59.png 由此，我们可以得到如下的运算关系，变换后的坐标我们运用了齐次坐标的性质都乘上了 z

\begin{pmatrix} nx \\ ny \\ unknown \\ z \\ \end{pmatrix} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \\ \end{pmatrix}

接下来运用任何在近平面上的点经过变化后不变和齐次坐标同乘 n 仍然表示同一个点

\begin{pmatrix} x \\ y \\ n \\ 1 \\ \end{pmatrix} \Rightarrow \begin{pmatrix} nx \\ ny \\ n^2 \\ n \\ \end{pmatrix}

我们可以得到之前？的那一行满足如下方程

\begin{pmatrix} A & B & C & D\\ \end{pmatrix} \begin{pmatrix} x \\ y \\ n \\ 1 \\ \end{pmatrix} = n^2 \Rightarrow A = B = 0,\space\space Cn + D = n^2

最后再利用远平面上的点 z 坐标不变的性质，可以得到如下方程

\begin{pmatrix} 0 & 0 & C & D\\ \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\ f \\ 1 \\ \end{pmatrix} = f^2 \Rightarrow Cf + D = f^2 \Rightarrow C = n + f,\space\space D = -nf

至此，我们得到这个“压缩”矩阵为

M_{persp\to otho} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & -nf \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}

最后我们讨论下课上的一个问题：位于远近平面 n 和 f 之间的一个点经过变换后会更靠近 n 还是 f 呢？经过计算可以得到“压缩”后的坐标为

\begin{pmatrix} nx \\ ny \\ (n + f)z -nf \\ z \\ \end{pmatrix} = \begin{pmatrix} \frac{nx}{z} \\ \frac{yx}{z} \\ \frac{(n + f)z -nf}{z} \\ 1 \\ \end{pmatrix}

我们要判断的即为 $\frac{(n + f)z -nf}{z} - z$ 的正负，值得一提的是，因为我们看向的是 -z 方向，所以越远反而 z 坐标越小，且 z 位于近平面与远平面之间应满足 $f \leq z \leq n \leq 0$ 。我们将上式乘上 -z 可以得到

-z\Delta_z = -(n + f)z + nf + z^2 = (z-n)(z-f) \leq 0

综上，我们知道变换后的点 z 坐标会变小，而 z 坐标变小代表离我们的相机变得更远了（别忘了是看像 -z 方向哦～）