符号约定

别名

$a:=b=f(x)$ ： b的定义是f(x), a是b的别名

sigmoid

sigmoid简写为 σ, 其原始定义为： $σ(x)=\frac{e^x}{e^0+e^x}$

σ化简为: $σ(x)=\frac{1}{e^{-x}+1}$

层

输入层为X，输入层为第0层

第0层X经过第1层权重$W^{(1)}$的线性变换 ，得到 第1层线性变换输出$O^{(1)}$ ，$O^{(1)}$经过第1层非线性函数sigmoid挤压输出第1层激活值$A^{(1)}$

softmax

向量x，对向量x的第i个分量做softmax的定义：

$softmax(x,x_{i})$=$\frac{ e^{ x_i } } { \sum\limits_{k} e^{ x_k } }$ : 此结果是单个实数(标量)

向量x，对向量x做softmax定义为 对向量x的每个分量做softmax:

$softmax(x) = [softmax(x,x_1) , softmax(x,x_2) ,..., softmax(x,x_N) ]$

cross_entropy

两个离散概率分布y、ŷ的交叉熵定义如下：

cross_entropy(y,ŷ) = $y_1log(ŷ_1)+y_2log(ŷ_2)+...+y_nlog(ŷ_C)$

两个离散分布的交叉熵 衡量 这两个分布的相似度，类似于 这两个分布的距离 ，

但是交叉熵很明显不满足距离三公理中的对称性的。

从交叉熵的式子看，其定义式应该是从以下原始定义式子简化而来，原始定义式如下：

ce(y,ŷ) = ${ŷ_1}^{y_1} {ŷ_2}^{y_2} ... {ŷ_n}^{y_C}$

对 ce(y,ŷ) 取对数，即可得到 cross_entropy(y,ŷ)

nn举例

训练集：X, Y

输入层： $X:=A^{(0)}$

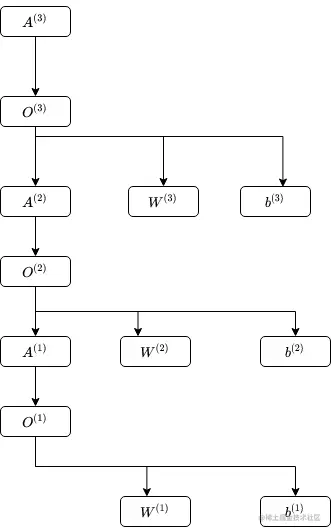
layer1： $O^{(1)}=XW^{(1)}+b^{(1)}$ ， $A^{(1)}=σ(O^{(1)})$

layer2： $O^{(2)}=A^{(1)}W^{(2)}+b^{(2)}$ ， $A^{(2)}=σ(O^{(2)})$

layer3： $O^{(3)}=A^{(2)}W^{(3)}+b^{(3)}$ ， $Ŷ:=A^{(3)}=softmax(O^{(3)})$

损失： J:=Loss=cross_entropy(Y, Ŷ)

注意 损失J 是单个实数（是标量），而非向量

尺寸

训练集中样本数为B (隐含意思是一个批次大小为B)

假设 B=2, 即训练集中只有2个样本：

X = $[x^{(1)}, x^{(2)}]$，Y=$[y^{(1)}, y^{(2)}]$

单个样本$x^{(i)}$的维度为N:

$x^{(i)}=[x^{(i)}_1, x^{(i)}_2, ..., x^{(i)}_N ]$

y为one-hot编码，类别个数为C，假设C=10，即共10个类别：

$y^{(i)}=[y^{(i)}_1, y^{(i)}_2, ..., y^{(i)}_{10} ]$

偏导 $\frac{∂J}{∂W}$ ， $\frac{∂J}{∂b}$

J -> $w^{(1)}_{1}$ , 此路径如下：

J -> $A^{(3)}$ -> $O^{(3)}$ -> $A^{(2)}, W^{(3)}, b^{(3)}$

$A^{(2)}$ -> $O^{(2)}$ -> $A^{(1)}, W^{(2)}, b^{(2)}$

$A^{(1)}$ -> $O^{(1)}$ -> $W^{(1)}, b^{(1)}$