「这是我参与2022首次更文挑战的第6天，活动详情查看：2022首次更文挑战」

一、引入

1.1 信号分解的基本思想

信号分析的基本思想之一是将复杂信号用基本信号表示，这样就能通过简单信号的性质来分析复杂信号。这里要求基本信号应具有：（1）由这些基本信号能够构成相当广泛的一类信号（2）线性时不变系统(LTIS)对基本信号的响应应当十分简单，以使其对任意输入信号的响应都有很方便的表达式

举例而言，基本信号可以是冲激函数

x\left( t \right) =\int{x\left( \tau \right)}\delta \left( t-\tau \right) d\tau

上式即为连续时间信号的冲激分解，利用的是冲激函数的采样性质

将信号冲激分解后，就可以简单地利用冲激响应来表示输出：

y\left( t \right) =\int{x\left( \tau \right)}h\left( t-\tau \right) d\tau

1.2 系统特征函数

若系统对一个信号的响应仅为一个常数乘以该信号，则称该信号为此系统的特征函数，这个常数可以视作幅度因子，定义为特征值

1.3 复指数分解

按照1.1的思路，考察具有类似性质的基本信号——复指数 设激励 $x\left( t \right) =e^{st}\,\, s\in C$ ，则输出通过上面说的冲激响应表示为：

y\left( t \right) =\int{h\left( \tau \right)}x\left( t-\tau \right) d\tau =e^{st}\int{h\left( \tau \right) e^{-s\tau}}d\tau =e^{st}H\left( s \right)

按照1.2的定义知道，复指数信号为LTIS的特征函数，对任一给定的 $s$ ，常数 $H(s)$ 为特征值；而对于一般的 $s$ ， $H(s)$ 为关于 $s$ 的函数，称为系统函数，当 $s$ 为纯虚数时， $H(jw)$ 称为系统频率响应，下面要引入的傅里叶分析都是建立在 $s=jw$ 的基础上，当 $s$ 为一般复数时，考察的是拉普拉斯变换，本文不赘述。

那么复指数是否满足1.1节基本信号的要求呢？

为便于理解，先给出离散信号 $x\left( t \right) =\sum_k{c_k}e^{s_kt}$ ，则响应 $y\left( t \right) =\sum_k{c_kH\left( s_k \right)}e^{s_kt}$ ，即若信号可以进行复指数分解，则响应可表示为相同复指数的线性组合，系数与输入和频率响应相关

可见，复指数信号完美地符合了1.1的要求，在此基础上就建立起了傅里叶分析。

二、周期信号的傅里叶级数

2.1 谐波复指数集

设 $x_0\left( t \right) =e^{j\omega _0t}$ ，定义基波频率为 $\omega _0$ ，基波周期为 $T_0$ 令谐波信号集：

\psi _k\left( t \right) =e^{jk\omega _0t}, k=0,\pm 1,\pm 2\cdots

其中 $k=0$ 时为直流分量， $k=\pm N$ 时为 $N$ 次谐波分量注意到谐波复指数集中，每一个信号都可以 $T_0$ 为周期，这是因为：

\psi _k\left( t \right) =e^{j\left( k\omega _0 \right) t}\\\Rightarrow T_k=\frac{2\pi}{|k|\omega _0}=\frac{T_0}{|k|}

即每经过一个 $T_0$ ，相当于经过了 $|k|$ 个相应的谐波周期。因此，谐波复指数集的线性组合也就以 $T_0$ 为周期：

x\left( t \right) =\sum_{k=-\infty}^{+\infty}{a_k}e^{jk\omega _0t}\,\, \left( 1 \right)

2.2 傅里叶级数

2.2.1 表示形式

在信号 $x(t)$ 可以复指数分解的条件下研究此问题。考察(1)式，现实中绝大多数信号为实信号，因此认为 $x(t)$ 为实数，满足：

\overline{x\left( t \right) }=\overline{\sum_{k=-\infty}^{+\infty}{a_k}e^{jk\omega _0t}}

由 $x\left( t \right) =\overline{x\left( t \right) }$ 导出：

x\left( t \right) =\sum_{k=-\infty}^{+\infty}{\overline{a_{-k}}e^{jk\omega _0t}}

进一步：

x\left( t \right) =a_0+\sum_{k=1}^{+\infty}{\left[ a_ke^{j\left( k\omega _0 \right) t}+\overline{a_ke^{j\left( k\omega _0 \right) t}} \right]}\\=a_0+2\sum_{k=1}^{+\infty}{\text{Re}\left\{ a_ke^{j\left( k\omega _0 \right) t} \right\}}

若 $a_k$ 以极坐标形式给出，即 $a_k=A_ke^{jw_0}$ ，此时

x\left( t \right) =a_0+2\sum_{k=1}^{+\infty}{A_k\cos \left[ \left( k\omega _0 \right) t+\theta _k \right]}\,\,\,\left( 2 \right)

若 $a_k$ 以笛卡尔坐标形式给出，即 $a_k=B_k+jC_k$ ，此时

x\left( t \right) =a_0+2\sum_{k=1}^{+\infty}{\left[ B_k\cos \left( k\omega _0t \right) -C_k\sin \left( k\omega _0t \right) \right]}\,\,\,\left( 3 \right)

对于周期函数，(1)式即为傅里叶级数的复指数形式；(2)式为傅里叶级数的三角形式(极坐标下)；(3)式为傅里叶级数的三角形式(笛卡尔坐标下)。一般地，若信号能展开为傅里叶级数，其表示形式必为(1)(2)(3)之一

2.2.2 收敛条件

并非所有周期信号都可以级数展开，即，并非所有信号都可以进行复指数分解。一般而言，满足Dirchlet条件的信号必可进行傅里叶分析，不满足Dirchlet条件的信号没有傅里叶级数形式，但可能有傅里叶变换。

Dirchlet条件 (1)信号绝对可积 (2)在任何有限区间内，信号只有有限个最值 (3)在任何有限区间内，信号只有有限个不连续点，且每个不连续点处都只有有限值

2.2.3 傅里叶系数

若信号满足Dirchlet条件，必能复指数分解为：

x\left( t \right) =\sum_{k=-\infty}^{+\infty}{a_k}e^{jk\omega _0t}

现在问题在于傅里叶系数 $a_k$ 的确定，可以采用以下方式求得：

e^{-j\left( n\omega _0 \right) t}x\left( t \right) =\sum_{k=-\infty}^{+\infty}{a_k}e^{j\left( k-n \right) \omega _0t}\,\,

两边同时在基波周期内积分：

\int_T{e^{-j\left( n\omega _0 \right) t}x\left( t \right)}dt=\sum_{k=-\infty}^{+\infty}{\int_T{a_ke^{j\left( k-n \right) \omega _0t}dt}}\,\,\\\Rightarrow \int_T{e^{-j\left( n\omega _0 \right) t}x\left( t \right)}dt=\sum_{k=-\infty}^{+\infty}{a_k\int_T{\left[ \cos \left( k-n \right) w_0t+j\sin \left( k-n \right) w_0t \right] dt}}\,\,

2.1节说过，谐波复指数集共同周期是基波周期，而三角函数一个周期内积分为0，在这里 $T=|k-n|T_k$ ，因此等式左边在 $k\ne n$ 时为0， $k=n$ 时为 $T$ ，即：

\int_T{e^{-j\left( n\omega _0 \right) t}x\left( t \right)}dt=a_nT

由于 $k=n$ ，所以改写为：

a_k=\frac{1}{T}\int_T{e^{-j\left( k\omega _0 \right) t}x\left( t \right)}dt\,\, \left( 4 \right)

此式即为傅里叶系数求解公式。

三、傅里叶变换

3.1 周期矩形脉冲信号

按照(4)式求解其傅里叶系数，得到：

a_k=\frac{2E\sin \left( k\omega _0T_1 \right)}{k\omega _0T}

从两个角度审视此式：

视其为关于 $k$ 的函数，即

a(k)=\frac{2E\sin \left( k\omega _0T_1 \right)}{k\omega _0T}

此时相当于将傅里叶系数等距离地排列在 $k$ 轴上，因此当 $T$ 趋于无穷时， $|a_k|$ 趋于0，即非周期信号的傅里叶系数幅度趋于0，正因如此，在幅度频谱中就看不出任何信息，所以对于非周期信号，不能仅关注 $a_k$

视其为包络线的采样

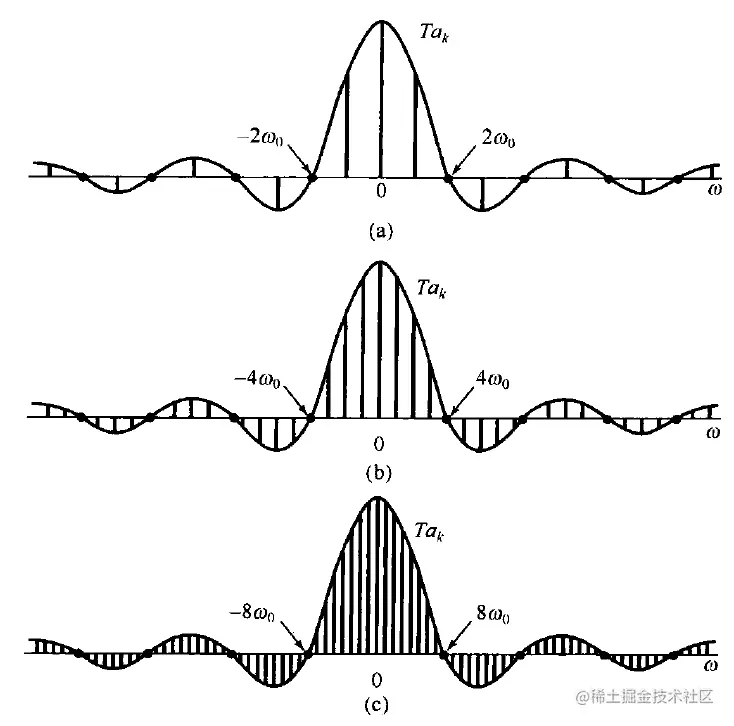
此时，视为：

a_kT=\frac{2E\sin \left( \omega T_1 \right)}{\omega}\mid_{w=kw_0}^{}

考虑关于 $w$ 的函数 $f\left( w \right) =\frac{2E\sin \left( \omega T_1 \right)}{\omega}$ ， $a_kT$ 就表示对 $f(w)$ 上 $w=kw_0$ 的位置进行采样。显然上面的采样间隔为 $w_0=2\pi/T$ ，因此随着 $T$ 不断增大，就出现了图2(a)->(c)取样变密的现象

重点理解的地方来了！！

注意这里 $T$ 趋于无穷时， $|a_k|$ 依然趋于0，但可见的是 $|a_k|T$ 是有限值(落在 $f(w)$ 上)，因此 $|a_k|T$ 的意义就是在 $|a_k|$ 趋于0的情况下，通过T的加权作用，在一个有限的范围内显示出 $|a_k|$ 间的相对大小关系，简言之， $|a_k|T$ 把肉眼不可见的非周期信号的傅里叶系数放大到肉眼可见，这其实就是傅里叶变换的引入基础。

3.2 傅里叶变换对

从3.1节知道，傅里叶变换的出发点，就是傅里叶系数的幅度加权与包络采样，因此： $X\left( w \right) \mid_{w=kw_0}^{}=a_kT$

从而，

X\left( w \right) =\int\limits_{-\infty}^{+\infty}{x\left( t \right) e^{-jwt}}dt\,\, \left( 5 \right)

代入 $x\left( t \right) =\sum_{k=-\infty}^{+\infty}{a_k}e^{jk\omega _0t}$ 中即得：

x\left( t \right) =\frac{1}{2\pi}\int\limits_{-\infty}^{+\infty}{X\left( w \right) e^{jwt}}dw\,\, \left( 6 \right)

(5)(6)式合称为一对傅里叶变换对，(5)式称为傅里叶变换积分

四、傅里叶级数与傅里叶变换的联系

4.1 信号三参数

这里定义信号的三参数为幅度、初相、频率(或角频率)，在傅里叶分析中，只要确定组成信号的所有复指数信号的三参数，就可以完全表征。无论是傅里叶级数还是傅里叶变换，事实上都是在求一个包含三参数的表达式来表示一个信号。

在傅里叶级数展开中，傅里叶系数表示了在频率 $w=kw_0$ 时复指数信号的幅度和相位；在傅里叶变换中，傅里叶积分 $X(w)$ 表示了全频率复指数信号的三参数信息——可以认为是公式化的频谱

具体来说，列于下表：

	幅度	相位	频率
$a_k$	绝对值	绝对值
$X(w)$	加权相对值	绝对值	绝对值

事实上，不应该以信号的周期与否来割裂傅里叶变换与傅里叶级数。换言之，周期信号与非周期信号都有相应的傅里叶变换和傅里叶系数，只不过周期信号的傅里叶变换为冲激函数的线性组合，非周期信号的傅里叶系数趋于0，但有相对大小。

4.2 几何直观

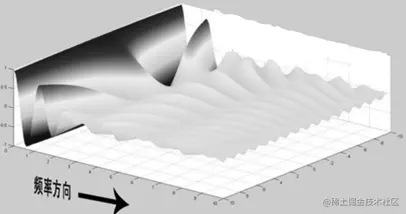
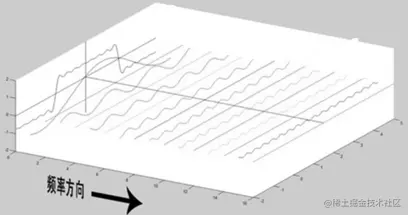
几何直观上，傅里叶变换是连续函数，因为其对象是全频率；傅里叶级数是离散的，因为其对象是采样的部分频率。

欢迎来我的AI频道"AI技术社"

深刻理解傅里叶级数与傅里叶变换的联系+推导、知识点串讲