这是我参与2022首次更文挑战的第9天,活动详情查看:2022首次更文挑战 | 创作学习持续成长,夺宝闯关赢大奖 - 掘金 (juejin.cn)
题目链接
- 删除最外层的括号 leetcode-cn.com/problems/re…
- 移除无效的括号 leetcode-cn.com/problems/mi…
- 基本计算器II leetcode-cn.com/problems/ba…
- 函数的独占时间 leetcode-cn.com/problems/ex…
- 表现良好的最长时间段 leetcode-cn.com/problems/lo…
题解及分析
删除最外层的括号
有效括号字符串为空 ""、"(" + A + ")" 或 A + B ,其中A和B都是有效的括号字符串,+代表字符串的连接。
例如,"","()","(())()" 和 "(()(()))" 都是有效的括号字符串。
如果有效字符串 s 非空,且不存在将其拆分为 s = A + B 的方法,我们称其为原语(primitive),其中 A 和 B 都是非空有效括号字符串。
给出一个非空有效字符串 s,考虑将其进行原语化分解,使得:s = P_1 + P_2 + ... + P_k,其中 P_i 是有效括号字符串原语。
对 s 进行原语化分解,删除分解中每个原语字符串的最外层括号,返回 s 。
这道题是 递归与栈拷问专题一 - 掘金 (juejin.cn)第5题的升级版,我们需要找出内层的内容并返回(题目能别说的那么复杂吗)
思路:
- 维护一个计数器
- 当遍历到左括号且计数器大于1,说明外部最少有一个左括号,我们把左括号拼接到字符串上
- 当遍历到右括号且计数器大于2,说明外部最少有一个右括号,拼接到字符串上
var removeOuterParentheses = function(s) {
let count = 0
let result = ''
for(let i = 0; i < s.length; i++) {
if(s[i] === '(' && count++ > 0) {
result += s[i]
} else if(s[i] === ')' && count-- > 1) {
result += ')'
}
}
return result
}
移除无效的括号
给你一个由 '('、')' 和小写字母组成的字符串s。
你需要从字符串中删除最少数目的'(' 或者 ')'(可以删除任意位置的括号),使得剩下的「括号字符串」有效。
请返回任意一个合法字符串。
有效「括号字符串」应当符合以下任意一条 要求:
- 空字符串或只包含小写字母的字符串
- 可以被写作 AB(A 连接 B)的字符串,其中 A 和 B 都是有效「括号字符串」
- 可以被写作 (A) 的字符串,其中 A 是一个有效的「括号字符串」
这是上一题的强化版,题目要求我们有选择的去除某些没有被闭合的括号 思路:
- 维护一个栈,我们将左括号的下标存入栈
- 当遇到右括号时,我们弹出栈顶的下标
- 遍历栈,将栈中对应存放的下标取出,删去对应的左括号
var minRemoveToMakeValid = function(s) {
let stack = []
const str = s.split('')
// 先取出多余的)
for(let i = 0; i < str.length; i++) {
if(str[i] === '(') {
stack.push(i)
} else if(str[i] === ')') {
if(stack.length) {
stack.pop()
} else {
str[i] = ''
}
}
}
// 再处理多余的(
let stackLen = stack.length
if(stackLen) {
for(let i = 0; i < stackLen; i++) {
str[stack[i]] = ''
}
}
return str.join('')
};
另一种写法:
var minRemoveToMakeValid = function(s) {
const leftDel = []
const rightDel = []
for(let i = 0; i < s.length; i++) {
if(s[i] === '(') {
leftDel.push(i)
} else if(s[i] === ')') {
if(leftDel.length) {
leftDel.pop()
} else {
rightDel.push(i)
}
}
}
const res = [...s]
const del = leftDel.concat(rightDel)
for(let i =0; i< del.length; i++) {
res[del[i]] = ''
}
return res.join('')
};
基本计算器II
给你一个字符串表达式
s,请你实现一个基本计算器来计算并返回它的值。 整数除法仅保留整数部分。
这道题需要的注意的是,我们需要考虑在什么时机执行计算,实际上,我们需要在遍历到下一个数字位的时候才执行之前记录的符号和数字的换算
思路
- 我们维护一个栈,一个前置符号,一个前置值记录
- 栈存入每一次运算的结果
- 使用栈的原因:首先操作的必定是最近的一个数字,可以直接从栈顶弹出;其次栈可以用来处理乘除优先级问题
- 前置符号用来判断上一次是什么结果,只有遍历到下一位时才进行判断
- 前置值用来记录上一位数
var calculate = function(s) {
s = s.trim()
const stack = []
let num = 0
let preSign = '+'
for(let i = 0; i < s.length; i++) {
if(!isNaN(Number(s[i])) && s[i] !== ' ') {
// 处理s多位数的情景
num = num * 10 + s[i].charCodeAt() - '0'.charCodeAt()
}
if(isNaN(Number(s[i])) || i === s.length - 1) {
switch (preSign) {
case '+':
stack.push(num);
break;
case '-':
stack.push(-num);
break;
case '*':
stack.push(stack.pop() * num);
break;
default:
stack.push(stack.pop() / num | 0);
}
preSign = s[i];
num = 0
}
}
let result = 0
while(stack.length) {
result += stack.pop()
}
return result
};
函数的独占时间
有一个单线程CPU正在运行一个含有n道函数的程序。每道函数都有一个位于0和n-1之间的唯一标识符。
函数调用 存储在一个调用栈上 :当一个函数调用开始时,它的标识符将会推入栈中。而当一个函数调用结束时,它的标识符将会从栈中弹出。标识符位于栈顶的函数是 当前正在执行的函数。每当一个函数开始或者结束时,将会记录一条日志,包括函数标识符、是开始还是结束、以及相应的时间戳。
给你一个由日志组成的列表 logs ,其中logs[i] 表示第i条日志消息,该消息是一个按 "{function_id}:{"start" | "end"}:{timestamp}" 进行格式化的字符串。例如,"0:start:3" 意味着标识符为 0 的函数调用在时间戳 3 的 起始开始执行 ;而 "1:end:2" 意味着标识符为1的函数调用在时间戳2的末尾结束执行。注意,函数可以 调用多次,可能存在递归调用 。
函数的独占时间定义是在这个函数在程序所有函数调用中执行时间的总和,调用其他函数花费的时间不算该函数的独占时间。例如,如果一个函数被调用两次,一次调用执行2单位时间,另一次调用执行1单位时间,那么该函数的独占时间为2 + 1 = 3 。
以数组形式返回每个函数的独占时间,其中第 i 个下标对应的值表示标识符 i 的函数的独占时间。
示例 1: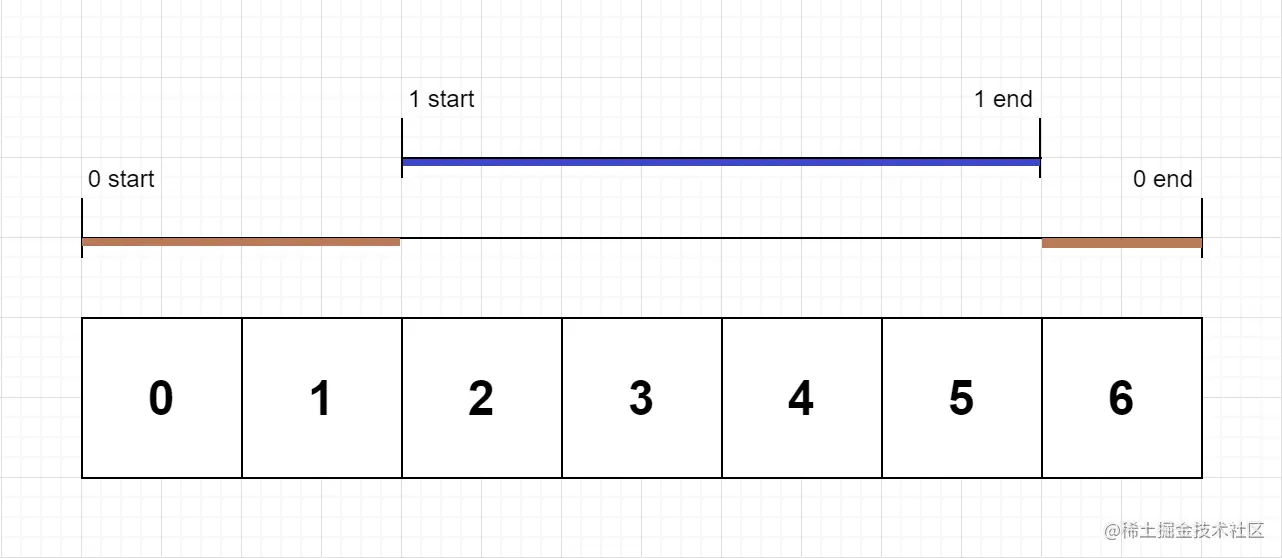
输入:n = 2, logs = ["0:start:0","1:start:2","1:end:5","0:end:6"]
输出:[3,4]
解释:
函数 0 在时间戳 0 的起始开始执行,执行 2 个单位时间,于时间戳 1 的末尾结束执行。
函数 1 在时间戳 2 的起始开始执行,执行 4 个单位时间,于时间戳 5 的末尾结束执行。
函数 0 在时间戳 6 的开始恢复执行,执行 1 个单位时间。
所以函数 0 总共执行 2 + 1 = 3 个单位时间,函数 1 总共执行 4 个单位时间。
不难看出题目如下要求:
- 单位时间分为start,end两部分
- start标记的时间段不仅代表任务开始时间,也代表任务开始执行
- end标记任务的结束,同时也代表某个时间段的结束,其后续任务需要从下个单位时间的start开始
- 任务执行期间如果有其他的任务插入,则前一个任务暂停,直至现任务执行完再继续执行上一个任务
- 递归任务也需要end两次
思路: 既然任务存在插入,同时也有插入的情况,那么记录这个流程的值需要用栈来处理
- 维护一个栈来保存不同的id,用一个数组来保存不同id对应的不同值
- 每次遍历时,如果遍历到start,则需要将当前执行到的任务id存入,如果栈中已经有值,则对上一个任务id(栈顶)进行计算并存入
- 如果遍历到end,则直接计算栈顶任务id的时间
var exclusiveTime = function(n, logs) {
const stack = []
const ans = new Array(n).fill(0)
let prev = 0
for(let i = 0; i < logs.length; i++) {
let [id, action, pos] = logs[i].split(':')
// *1主要为了处理0的问题
id *= 1
pos *= 1
if(action === 'start') {
if (stack.length) {
// 对应插入任务和递归任务
ans[stack[stack.length - 1]] += pos - prev;
}
prev = pos;
stack.push(id);
} else {
ans[stack[stack.length - 1]] += pos - prev + 1
stack.pop()
prev = pos + 1
}
}
return ans
};
折腾下,整个递归写法,思路变化的地方在于,不在试图用栈保存id,而是去找下一个start的时间点(时间段是连贯的)
var exclusiveTime = function(n, logs) {
const res = new Array(n).fill(0)
let go = 0
function next() {
// 记录子任务花费的时长
let dure = 0
const start = logs[go].split(':')
// 获取go指向的任务到下一个start的时间
while(go < logs.length - 1 && logs[go + 1].indexOf('s') !== -1) {
go++
dure = dure + next()
}
const end = logs[++go].split(':')
let sum = Number(end[2] - Number(start[2])) + 1 - dure
res[Number(start[0])] = res[Number(start[0])] + sum
return sum + dure
}
while(go < logs.length) {
next()
go++
}
return res
};
表现良好的最长时间段
给你一份工作时间表hours,上面记录着某一位员工每天的工作小时数。
我们认为当员工一天中的工作小时数大于8小时的时候,那么这一天就是「劳累的一天」。
所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格大于「不劳累的天数」。
请你返回「表现良好时间段」的最大长度。
题目实际上并没有多复杂,但是这道题对算法的优化上能做的事情比较多 题目的重点是:「劳累的天数」是严格大于「不劳累的天数」,即工作时间大于8小时的天数要大于工作时间小于等于8小时的天数(呵,来自资本的剥削)
思路 这道题算法略微复杂一些,分成四个阶段:
1.将每个值是否大于8标识出来,大于8标记为1,否则标记为-1
- 这么做的意义是,将数组中每个值从判断是否大于8抽象成一个数字标识 2.用一个数组prefixSum计算数组中值累加的情景
- 很经典的前缀数组算法
- 这一步的作用是,计算出第一天到第n天是否表现良好时间段的数字标识
- 这么做的意义是,具象化数组元素间的关系,后续只需要对数组中的某段数据进行计算即可
- 前两步操作之后,数组时间被完整抽象成经过处理的多个时间段累计 3.找到每个(i,j)使得prefixSum[j] - prefixSum[i] > 0,将j下标存入存入栈stack中
- 实际上,这一步隐藏的条件是prefixSum[j] > 0,但是prefixSum第一位是0
- 这一步的作用,是筛选出表现良好时间段,即值大于0的区间
- prefixSum[j] - prefixSum[i] > 0推断依据如下
- 数学上,任意一个i < j1 < j2, 如果prefixSum[i] < prefixSum[j2], 那么(i,j1)一定不会是答案
- 数学上,对于任意的一个i < i1 < j, 如果prefixSum[i1] >= prefixSum[i],那么(i1, j)一定不会是答案
- 由于标记值是-1和1,因此即便i和j相邻,也不会出现相等的情景
- prefixSum的第一个元素刚好是0,那么只要大于这个值都是符合题意的备选答案 4.倒序遍历prefixSum,将stack中的下标取出并比较取最大值
- 倒序的原因,是因为题目需要最长时间,我们直接从最后一天开始倒推
- 这一步的作用是比较
更详细的讲解: 参考了几个大神的题解之后总结下来非常详细的解题思路, 希望大家少走些弯路. - 表现良好的最长时间段 - 力扣(LeetCode) (leetcode-cn.com)
var longestWPI = function(hours) {
const arr = []
for(let i of hours) {
if(i > 8) arr.push(1)
else arr.push(-1)
}
const prefixSum = []
let cur_sum = 0
for(let i of arr) {
prefixSum.push(cur_sum)
cur_sum += i
}
// 第一位相加时cur_sum = 0,最后再补入一位
prefixSum.push(cur_sum)
// 找到一个(i,j)使得prefixSum[j] - prefixSum[i] > 0
const stack = []
for(let i of prefixSum) {
if(!stack.length || prefixSum[stack[stack.length - 1]] > i) {
// 因为题目要求查找最长距离,因此这里记录的是下标
stack.push(i)
}
}
let res = 0
for(let i = prefixSum.length - 1; i > 0; i-- ) {
while(stack.length && prefixSum[i] > prefixSum[stack[stack.length - 1]]) {
res = Math.max(res, i - stack[stack.length - 1])
stack.pop()
}
}
return res
};
题目总结
在判断使用栈解决问题的时候,我们面临的问题往往是什么时候才是合适的栈弹出时机?甚至在最后一道题,栈仅仅是一个优化使用的工具。