是平平无奇的数学小天才啦🦖🦖🦖吼！吼！吼！

1 凸函数

1.1 凸集

对数据集合C，内的任意两点x1,x2∈C，那么连接x1,x2其连线上的点也属于集合C：

\theta x_1+( 1 - \theta) \in C (\forall 0 \le\theta \le 1)

一个集合中所有的数据，随机抽出两个数据，把这两个数据点相连，连线上的所有数据都在集合中。

画图代码:

import numpy as np
import matplotlib.pyplot as plt
pi,sin,cos = np.pi,np.sin,np.cos
r1 = 1
theta = np.linspace(0,2*pi,36)
x1 = r1*cos(theta)
y1 = r1*sin(theta)
plt.fill(x1,y1)

plt.show()

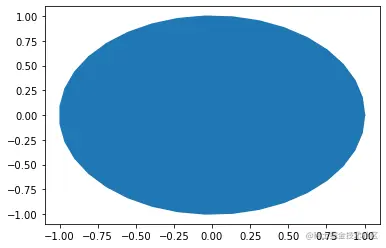
上图就是一个凸集，深色区域内任意两点连接，连线上的点都在深色区域内。

import numpy as np
import matplotlib.pyplot as plt
pi,sin,cos = np.pi,np.sin,np.cos
r1 = 1
r2 = 2
theta = np.linspace(0,2*pi,36)
x1 = r1*cos(theta)
y1 = r1*sin(theta)
x2 = r2*cos(theta)
y2 = r2*sin(theta)
plt.fill(x2,y2,'r')
plt.fill(x1,y1,'w')
plt.show()

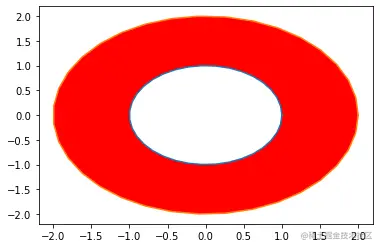
上面不是一个凸集，深色区域内任意两点连接，连线上的点不一定都在深色区域内。

1.2 凸函数

对定义在凸集上的函数 $f:R^d \mapsto R^1$ (意思是d维的x映射到1维的y上),均满足：

f(\theta x_1+( 1 - \theta)x_2)\le\theta f(x_1)+(1-\theta)f(x_2) (\forall 0 \le\theta \le 1)

其中 $\forall x,z ∈ \psi$ , $\psi$ 表示定义域

画图代码:

import numpy as np
import matplotlib.pyplot as plt
x = [i for i in range(20)]
x = np.array(x)
plt.plot(x,x*x*1/2)
plt.show()

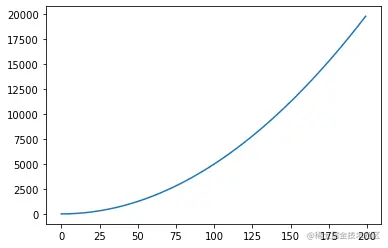
上面那个函数是 $f(x) = \frac{1}{2}x^{2}$ ,类似上图满足上面的公式都是凸函数，任意两点的连线都在函数上面。

1.3 梯度

多维函数 $x1+x2+x3..+xn = y$ 是可导的，他的各个方向的梯度就是对不同x的偏导。

\bigtriangledown f(x) = (\dfrac{\partial f(x)}{\partial x_1},\dfrac{\partial f(x)}{\partial x_2},....,\dfrac{\partial f(x)}{\partial x_n})

这就是梯度啦。

然后f(x)在x点泰勒展开是: $f(x) = f(x) + f^{'}(x-1)....$

关于凸函数,在f(x)上,随机取两个相邻的点 $x_{1}$ , $x_{2}$ ,不妨设 $x_{2} > x_{1}$ ,把 $f(x_{1})$ 加上 $f(x_{1})$ 相对 $f(x_{2})$ 增长的一部分就等于 $f(x_{2})$ 。

那么增长的一部分等于什么?

那肯定是 $f^{'}(x)$ 与x = x1,x = x2,y =0围成的面积啦。(为了方便这里只讨论二维)

那么当 $x_{2}$ 无限趋向于 $x_{1}$ 此时 $f^{'}(x)$ 是不变的 $f^{'}(x_{1}) = f^{'}(x_{2})$ ，此时定义域 $[x_{1},x_{2}]$ 内的所有对应的斜率为 $f^{'}(x_{1}).所以把$ f^{'}(x_{1}) $乘$ x_{2} - x_{1} $就等于$ f(x_{1}) $相对$ f(x_{2}) $增长的一部分就等于$ f(x_{2})$。

但是当 $x_{1}$ 与 $x_{2}$ 没有那么近的时候，凸函数的导数是不断变大的，也就是说 $f^{'}(x_{1})是小于$ f^{'}(x_{2})的，那么 $f(x_{1})$ 相对 $f(x_{2})$ 增长的一部分是大于 $f^{'}(x_{1})$ 乘 $x_{2} - x_{1}$ 的。

大家可以拿$ f(x) = \frac{1}{2}x^{2} $画一下草图

也就是下面这个式子:

f(x_2)\ge f(x_1) + \bigtriangledown f(x_1) ^T (x_2 -x_1)

从而我们可以知道，f(x)在定义域中任意点的一阶泰勒展开是其下界（你看他没加二阶三阶等肯定是少加了很多鸭)

1.4 强凸函数

咱们是做机器学习的，所以要严格一点，不仅要保证是凸函数，保证函数曲线在切线的上方，更要保证切线与函数是保持一定距离的，这个距离不是固定的，也是由一个函数来得到的。

符合下面公式的函数，我们称其为 $\lambda-$ 强凸函数:

f(x_2)\ge f(x_1) + \bigtriangledown f(x_1) ^T (x_2 -x_1) +\dfrac{\lambda }{2}|| x_2 - x_1||^T

其中 $\forall x,z ∈ \psi$ （ $\psi$ 表示定义域) ， ${\exists \lambda ∈ R_{+}}$ 。

也就是函数增加的必须大于某个数(这个数不是常数，是由某个函数得到的)，相应的凸函数公式也变为:

f(\theta x_1+( 1 - \theta)x_2)\le\theta f(x_1)+(1-\theta)f(x_2) - \dfrac{\lambda \Theta}{2} (1- \Theta) || x_2 - x_1||(\forall 0 \le\theta \le 1)

其中 $\forall x,z ∈ \psi$ （ $\psi$ 表示定义域) ， ${\exists \lambda ∈ R_{+}}$ 。

1.5 l-Lipschits连续

如果f(x)的局部变化不超过某个幅度， $x_1$ 是无限接近于 $x_2$ 。

那么 $\exists l∈R_{+}$ 使得 $\forall x_{1},x_{2} ∈ \psi$ ( $\psi$ 表示合集) 都有:

$f(x_2) - f(x_1) \le l||x_2 -x_1| |$

满足上面性质的函数我们称函数f(x)为 $l-光滑$

1.6 Hessian矩阵

Hessian矩阵是函数f(x)在定义域上的二阶导数的矩阵:

\bigtriangledown^2 f(x) \in R^d *R^d

如果f(x)的定义域是凸集，然后二阶导数大于0,数学表达是:

\bigtriangledown^2 f(x)\succeq0

那么f(x)就是是凸函数，Hessian矩阵是半正定的。

1.7 不改变凹凸性的数学变化

f是凸函数，f(Ax+B)也是凸函数
$f_1,f_2..f_n$ 是凸函数， $\omega_1,\omega_2...\omega_n \geq 0$ ,f(x) = $\sum_{i=1}^{N}\omega_nf_n$ 也是凸函数。
$f_1,f_2..f_n$ 是凸函数， $f(x) = max \{ f_1(x),f_2(x)..f_n(x) \}$ 也是凸函数
$\forall z ∈ X$ f(x,z)是关于x的凸函数,则 $g(x) = sup_{z∈X}f(x,z)$ 也是关于x的凸函数，(调参，任意一个z,或者说固定z的时候，都有一个x把函数f(x,z),调到上确界)

1.8 共轭函数

$f:R^d \mapsto R$ 定义为: $f_*(z) =sup (z^Tx - f(x))$

共轭函数反应的是线性函数 $z^Tx$ 与f(x)的最大差值。

比如: $f(x) = \frac{1}{2}x^{2}$ ，共轭函数 $f_*(z)$ 在 z = 2(固定z)的值,就等于2x与f(x)之间的最大差值,因为是凸函数， $f^{'}(x)$ 在定域内是单调递增的，当 $f^{'}(x) < 2$ 的时候f(x)与2x之间的差值是不断变大的，也就是说x<2的时候2x的导数更大，2x变化的更多，当 $f^{'}(x) > 2$ 的时候f(x)的导数更大，f(x)变化变化的更多，差值在变小，所以 $f^{'}(x) = 2$ 的时候差值最大.

共轭函数有很好的性质:

无论原函数是否是凸函数，共轭函数一定是凸函数。
若原函数可微，则:

f_*( \bigtriangledown f(x)) = \bigtriangledown f(x)^Tx-f(x)=-[f(x)+ \bigtriangledown f(x)^T(0-x)]

2 最优化基础

2.1 什么是最优化

相信各位都学过极值，我们的极值就是我们要求的一个最优解。

问题的最优解可以表达为:

f(x_0)\le f(x) ,x∈Ω

那么 $x_0$ 就是极小值，极大值类似，最优化就是找到这个极值。

函数可能有多个极值，我们希望找到函数里的最值，但是梯度下降等一些算法只能找到局部最优解，也就是这个局部的最值，不一定是全部的最值。

如果目标函数跟约束函数都是凸函数，那么这个问题就成了凸优化的问题了。

2.2 主问题与对偶问题

主问题就是：显式列出m个不等式约束和n个等式约束。写为：

\substack{\min\\x}\quad\quad\quad\quad f(x) \\ \quad\quad\quad\quad\quad s.t. \quad\quad\quad h_{i}(x) \geq 0 \quad(i∈[m]),\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad g_{j}(x) \geq 0 \quad(j∈[n]).

当主问题难解的时候，但是其对偶问题容易求解，且通过求解对偶问题能得到原始问题的最优解。

主(原)问题如何转换对偶问题？

(分界线)	原问题	对偶问题
决策变量	n个；>=0;<=0;无约束	n个；>=0;<=0; =0
线性约束	m个;<=0;>=0;=0	m个；>=0;<=0;无约束
目标	求max，系数是对偶问题中线性约束常数	求min，系数是原问题中线性约束常数

例子：

小明有一个打印机，可以用来赚钱。
把打印机出租给小杨，通过出租赚钱。

从小明的角度看不管是1，2哪个条件，小明是想最大化自己的利润，从小杨角度看，小杨是想最大化自己的收入，再联系现有条件，也就是看小杨的支付的最小租金。这就是一对对偶问题。

2.3 拉格朗日对偶

为什么需要使用拉格朗日对偶性把原始问题改为对偶问题?

答:无论原问题是什么形式，其对偶问题都是凸问题。

为什么对偶函数一定是凹函数？

答:

（这是我当初在csdn写的)

证明使用的公式：

\min \{a_i + b_j\} \le \min a_i + \min b_j \ \ \ \ \ \ \ \ i,j∈N^+

下面用图解释对偶函数是凹函数

画图代码:

import numpy as np
import matplotlib.pyplot as plt
a = np.linspace(0, 10, 1000)
y = 2*a
z = 3*a- 20
q = -9*a+ 12
x = a
plt.figure(figsize=(8,4))
plt.plot(x,y,color="black",linewidth=2)
plt.plot(x,y,x,z,x,q,color="black",linewidth=2)
plt.plot(x,q,color="black",linewidth=2)
plt.xlabel("α")
plt.ylabel("L")
plt.title("Example")
plt.show()

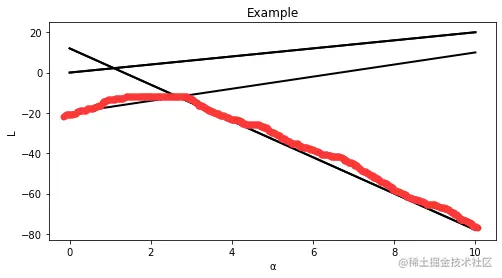
固定好 $\alpha$ ,在 $\alpha$ 相同的时候找L的最小值，就是我画的红线。

2.4 广义拉格朗日函数

可以用广义拉格朗日函数来找最值 $\lambda_i$ 与 $\mu$ 分别是针对不等式约束 $h_i(x) \le 0$ 和 $g_i(x) = 0$ 引入的拉格朗日乘子

L(x,\lambda,\mu)=f(x)+\sum_{i=0}^n \lambda_i h_i(x) +\sum_{j=0}^m \mu g_j(x)

相应的拉格朗日对偶函数为:

Г(\lambda,\mu) = \substack{\inf\\x∈\psi} L(x,\lambda,\mu) =\substack{\inf\\x∈\psi} (f(x)+\sum_{i=0}^n \lambda_i h_i(x) +\sum_{j=0}^m \mu_j g_j(x))

因为 $h_i(x) \le 0$ 与 $g_i(x) = 0$ ,所以 $\sum_{i=0}^n \lambda_i h_i(x) +\sum_{j=0}^m \mu g_j(x) \le 0$

对于 $x∈ \psi$ 有: $Г(\lambda,\mu) = \substack{\inf\\x∈\psi} L(x,\lambda,\mu) \le L(x,\lambda,\mu) \le f(x)$

所以拉格朗瑞对偶函数 $Г(\lambda,\mu)$ 给出了 $L(\lambda,\mu)$ 的目标函数f(x)最优值(设为 $p^*$ )的下界。

也就是 $\forall \lambda \succeq 0$ 都有 $Г(\lambda,\mu) \le p^*$ 。

设对偶函数 $Г(\lambda,\mu)$ 的目标函数的最优值是 $d^*$ ，则 $d^*$ 是 $p^*$ 的下界,也就是:

d^* \le p^*

这是弱对偶性

d^* = p^*

这是强对偶性,强对偶性一般不成立，但是若主问题为凸优化问题，且可行域中至少有一处使不等式约束严格成立，则强对偶性成立。

2.5 KKT条件

KKT条件主要是用来刻画主问题与对偶问题的最优解之间的关系，令 $x^*$ 为主问题的最优解， $(\lambda^*,\mu^*)$ 为对偶问题的最优解，当强对偶成立时：

f(x^*) = Г(\lambda^*,\mu^*) = \substack{\inf\\x∈\psi} L(x,\lambda,\mu) \le f(x^*)+\sum_{i=0}^n \lambda^*_i h_i(x^*) +\sum_{j=0}^m \mu^*_j g_j(x^*) \le f(x^*)

所以此时不等式应该取等号，所以下面两个条件应该成立:

互补松弛条件：

\lambda^*h_i(x^*) = 0 \ \ \ i∈[m](因为是m个不等式鸭)

也就是说这个时候 $\lambda^* > 0$ $h_i(x^*) = 0$ 或者 $\lambda^* \neq 0$ $h_i(x^*) = 0$

$x^*$ 是下面问题的最优解：

x^* = \substack{\arg \min\\x∈\psi}L(x,\lambda^*,\mu^*) =\substack{\arg \min\\x∈\psi} f(x)+\sum_{i=0}^n \lambda^*_i h_i(x) +\sum_{j=0}^m \mu^*_j g_j(x)

通常 $\psi$ 为全集或 $x^*$ 位于 $\psi$ 内部因此拉格朗日函数 $L(x,\lambda,\mu)$ 在 $x^*$ 处的梯度为0，也就是:

\nabla f(x^*)+\sum_{i=0}^n \lambda_i \nabla h_i(x^*) +\sum_{j=0}^m \mu_j \nabla g_j(x^*) = 0

所以KKT条件由以下几个部分组成:

主问题约束: $h_{i}(x^*) \geq 0 \quad(i∈[m])$ 和 $g_{j}(x^*) = 0 \quad(i∈[m])$
对偶问题约束: $\lambda^* \succeq 0$
互补松弛条件: $\lambda^* h_{i}(x^*) = 0\quad(i∈[m])$
拉格朗日函数在 $x^*$ 处的梯度为0: $\nabla f(x^*)+\sum_{i=0}^n \lambda_i \nabla h_i(x^*) +\sum_{j=0}^m \mu_j \nabla g_j(x^*) = 0$

KKT条件具有如下重要性质:

强对偶性成立时，对于任意的优化的问题，KKT条件是最优解的必要条件。
对于凸优化问题，KKT条件是充分条件，即满足KKT条件的解一定是最优解。
对于强对偶性成立的凸优化问题，KKT条件是充要条件，也就是当 $x^*$ 是原始问题的最优解当且仅当存在 $(\lambda^* ,\mu^*)$ 满足KKT条件。

3.参考:

[1].Matplotlib的文档

[2] 周志华王魏高尉张利军《机器学习理论导引》

机器学习初级入门(一)预备知识

1 凸函数

1.1 凸集

1.2 凸函数

1.3 梯度

1.4 强凸函数

1.5 l-Lipschits连续

1.6 Hessian矩阵

1.7 不改变凹凸性的数学变化

1.8 共轭函数

2 最优化基础

2.1 什么是最优化

2.2 主问题与对偶问题

2.3 拉格朗日对偶

2.4 广义拉格朗日函数

2.5 KKT条件

3.参考: