栈加强篇

下面题解中的栈都可以用数组来代替

化栈为队

• 链接 leetcode-cn.com/problems/im…
• 解题思路 两个栈，先入一个栈，然后再出栈并推入另一个栈，另一个栈再出栈，即可实现先进先出。

class Stack {
    constructor() {
        this.arr = [];
    }
    
    push(val) {
        this.arr.push(val);
    }
    
    pop() {
        return this.arr.pop();
    }
    
    peek() {
        return this.arr[this.arr.length - 1];
    }
    
    empty() {
        return this.arr.length === 0;
    }
}
/**
 * Initialize your data structure here.
 */
var MyQueue = function() {
    this.s1 = new Stack();
    this.s2 = new Stack();
};

/**
 * Push element x to the back of queue. 
 * @param {number} x
 * @return {void}
 */
MyQueue.prototype.push = function(x) {
    while(!this.s2.empty()){
        this.s1.push(this.s2.pop());
    }
    this.s1.push(x)
};

/**
 * Removes the element from in front of queue and returns that element.
 * @return {number}
 */
MyQueue.prototype.pop = function() {
    while(!this.s1.empty()){
        this.s2.push(this.s1.pop());
    }
    return this.s2.pop();
};

/**
 * Get the front element.
 * @return {number}
 */
MyQueue.prototype.peek = function() {
    while(!this.s1.empty()){
        this.s2.push(this.s1.pop());
    }
    return this.s2.peek()
};

/**
 * Returns whether the queue is empty.
 * @return {boolean}
 */
MyQueue.prototype.empty = function() {
    return this.s1.empty() && this.s2.empty();
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * var obj = new MyQueue()
 * obj.push(x)
 * var param_2 = obj.pop()
 * var param_3 = obj.peek()
 * var param_4 = obj.empty()
 */

验证栈序列

• 链接 leetcode-cn.com/problems/va…
• 解题思路 根据给定的序列入栈，如果入栈的数字和出栈序列的第一个一样，就出栈，最后栈中为空，则栈序列正确

 class Stack {
    constructor() {
        this.arr = [];
    }
    
    push(val) {
        this.arr.push(val);
    }
    
    pop() {
        return this.arr.pop();
    }
    
    peek() {
        return this.arr[this.arr.length - 1];
    }
    
    empty() {
        return this.arr.length === 0;
    }
}
var validateStackSequences = function(pushed, popped) {
    const stack = new Stack();
    for(let i = 0; i < pushed.length; i++) {
        stack.push(pushed[i]);
        while(popped[0] === stack.peek() && !stack.empty()) {
            stack.pop();
            popped.shift();
        }
    }
    if(stack.empty()) return true;
    return false;
};

1249. 移除无效的括号

• 链接 leetcode-cn.com/problems/mi…
• 解题思路 用栈来解决括号的匹配问题是最好使得，我们可以用两个栈来解决这个问题，一个栈用来处理括号的匹配，一个栈用来记录括号对应的索引，遍历字符串之后通过索引移除对应括号。

 class Stack {
    constructor() {
        this.arr = [];
    }
    
    push(val) {
        this.arr.push(val);
    }
    
    pop() {
        return this.arr.pop();
    }
    
    peek() {
        return this.arr[this.arr.length - 1];
    }
    
    empty() {
        return this.arr.length === 0;
    }
}
var minRemoveToMakeValid = function(s) {
    const indexStack = new Stack();
    const stack = new Stack();
    for(let i = 0; i < s.length; i++) {
        if(s[i] === '(') {
            stack.push(s[i]);
            indexStack.push(i);
            continue;
        }
        if( s[i] === ')' && stack.peek() === '(') {
            stack.pop();
            indexStack.pop();
            continue
        } 
        if(s[i] === ')'){
            stack.push(s[i]);
            indexStack.push(i);
        }
    }
    const res = s.split('');
    while(!indexStack.empty()) {
        const index = indexStack.pop();
        res[index] = '';
    }
    return res.join('')
};

验证二叉树的前序序列化

• 链接 leetcode-cn.com/problems/ve…
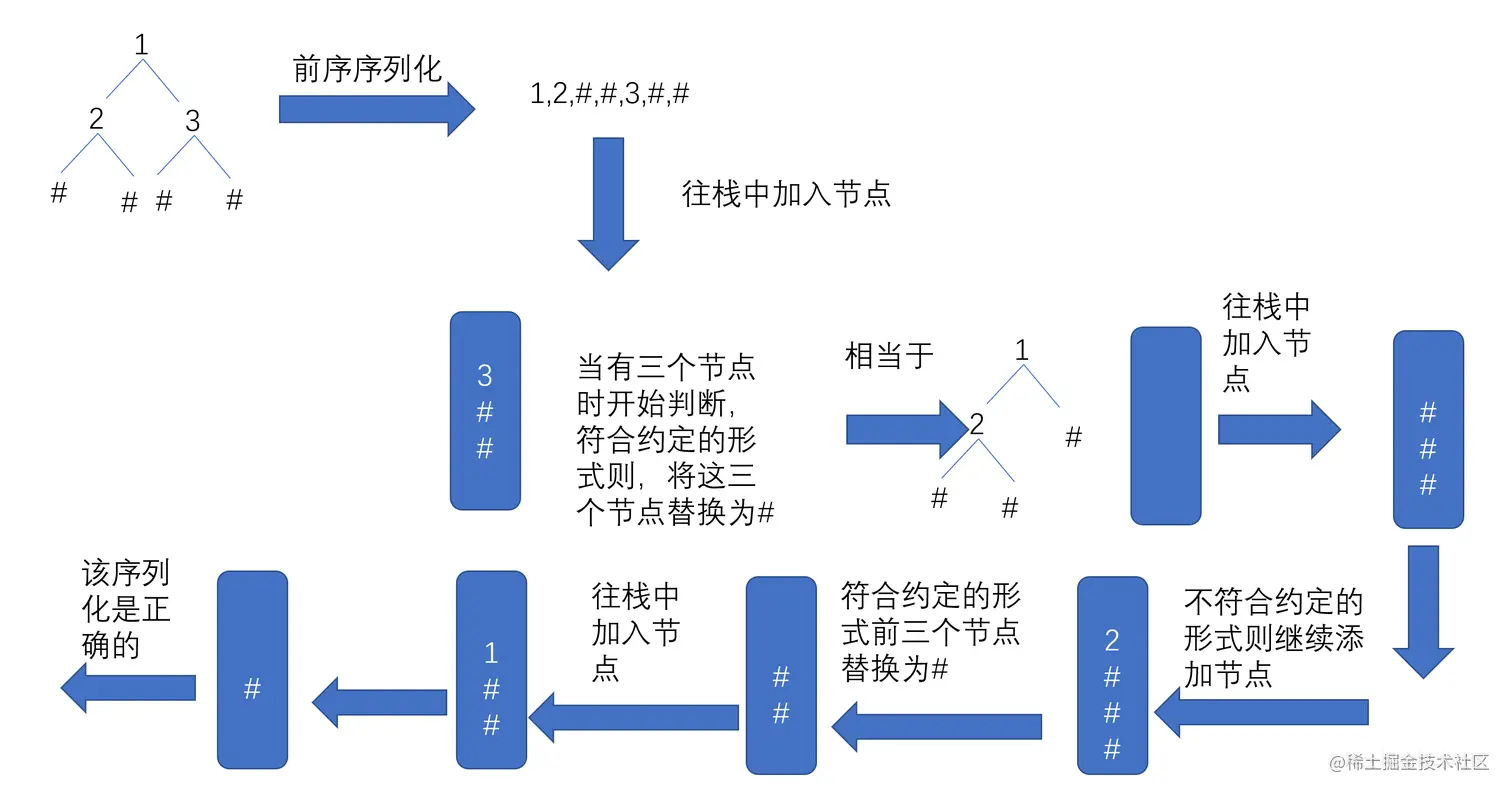
• 解题思路 根据题意可以反向推导，从最深的子节点开始，将最深的三个节点入栈，如果先入栈的两个元素是#，并且最后入栈的节点是数值，则说明这个节点是正常的，我们可以把这个节点替换成一个#，放回原来树中，如果前序遍历是合法的最后一定只剩一个#

class Stack {
    constructor() {
        this.arr = [];
    }
    
    push(val) {
        this.arr.push(val);
    }
    
    pop() {
        return this.arr.pop();
    }
    
    peek() {
        return this.arr[this.arr.length - 1];
    }
    
    empty() {
        return this.arr.length === 0;
    }
    size() {
        return this.arr.length;
    }
}
var isValidSerialization = function(preorder) {
    let arr = preorder.split(',');
    const stack = new Stack();
    while(arr.length>0) {
        stack.push(arr.pop());
        if(stack.size() > 2){
            const one = stack.pop();
            const two = stack.pop();
            const three = stack.pop();
            if(one !== two && two === three && three === '#'){
                stack.push('#');
            } else{
                stack.push(three);
                stack.push(two);
                stack.push(one);
            }
        }
    }
    return stack.pop() === '#' && stack.empty();
};

利用栈实现一个计算器

• 思路 通过分治的思想找出式子中优先级最低的运算符，对这个运算符两边的式子分别求值，最后对这两个值进行运算即可。

function calc(s) {
    s = s.trim()
    let sig = ''; // 运算符
    let sigIndex = 0;  // 运算符的位置
    let sigRank = 999; // 运算符的优先级
    let rank = 0; // 运算符外层的括号
    if(s[0] === '(' && s[s.length - 1] === ')') {
        const a = s.slice(1, s.length - 1);
        // 利用栈来检测去除括号之后的式子是否合法
        const stack = [];
        for(let i = 0; i < a.length; i++){
            if(a[i] === '('){
                stack.push(a[i]);
            }
            if(a[i] === ')' && stack[stack.length -1] === '('){
                stack.pop();
                continue;
            }
            if(a[i] === ')'){
                stack.push(a[i]);
            }
        }
        // 如果合法则去除括号
        if(stack.length === 0){
            s = a;
        }
    }
    // 找到优先级最低的运算符
    for(let i = 0 ; i < s.length; i++){
        // 如果有括号，对括号中的运算符优先级加100
        if(s[i] === '(') rank +=1;
        if(s[i] === ')') rank -=1;
        if(s[i] === '*' || s[i] === '/' || s[i] === '+' || s[i] === '-') {
            switch(s[i]) {
                case '+': 
                case '-': 
                    {
                        let curSigRank = 1 + rank * 100;  // 加减运算符优先级默认为1
                        if(curSigRank < sigRank) {
                            sigRank = curSigRank;
                            sig = s[i];
                            sigIndex = i;
                        }
                    }
                    break;
                case '*': 
                case '/':
                    {
                        let curSigRank = 2 + rank * 100; // 除运算符优先级默认2
                        if(curSigRank < sigRank) {
                            sigRank = curSigRank;
                            sig = s[i];
                            sigIndex = i;
                        }
                    }
                    break;
                default:
                    break;
            }
        }
    }
    if(!sig) return parseInt(s);
    const s1 = s.slice(0,sigIndex).trim();
    const s2 = s.slice(sigIndex+1).trim();
    const num1 = calc(s1);
    const num2 = calc(s2);
    switch(sig){
        case '*':
            return num1 * num2
        case '/':
            return num1 / num2
        case '+':
            return num1 + num2
        case '-':
            return num1 - num2
        default:
            break
    }
}