先验概率、后验概率、似然函数概念与联系「这是我参与2022首次更文挑战的第15天，活动详情查看：2022首次更文挑战」。

「这是我参与2022首次更文挑战的第15天，活动详情查看：2022首次更文挑战」。

本文解释了标题三个概念之间的关系，给出了后验概率的求法。

我们熟知的贝叶斯公式是这样的:

P(A \mid B)=\frac{P(B \mid A) * P(A)}{P(B)}

但在这里我们采用如下形式:

p(\theta \mid x)=\frac{p(x \mid \theta) p(\theta)}{p(x)}

贝叶斯公式是这几个概念的理论基础

可以把这里的 $\theta$ 理解为原因， $x$ 理解为结果，因为 $\theta$ 决定了 $x$ 是什么样的。

\text { 后验概率 }=\frac{\text { 似然估计 } * \text { 先验概率 }}{\text { 证据 }}

随后介绍概念，再使用一个例子加深理解

事情还没有发生，根据以往的经验来判断事情发生的概率，反映人们在抽样前对 θ 的认识。

扔一个硬币，在扔之前我们无法根据实验结果给出结果的概率分布；

但根据日常经验和对硬币的观察，我们可以假定正面向上的概率为0.5；

这里根据我们之前的经验得到的0.5就是先验概率。

事情已经发生了，导致事情发生的原因很多，根据结果来判断各个由不同原因导致的概率。

后验分布 p(θ|X) 是反映人们在抽样后对 θ 的认识，之间的差异是由于样本的出现后人们对 θ 认识的一种调整，所以后验分布 p(θ|X) 可以看作是人们用总体信息和样本信息（抽样信息）对先验分布 p(θ) 作调整的结果。

已经获得了样本，导致产生这些样本的原因很多，不同原因可以导致某个固定结果的概率。

用似然分布的方法根据样本确定参数的估计路数叫做似然估计，这种估计方式没有考虑先验知识，仅使用了获得的样本信息。

已知：

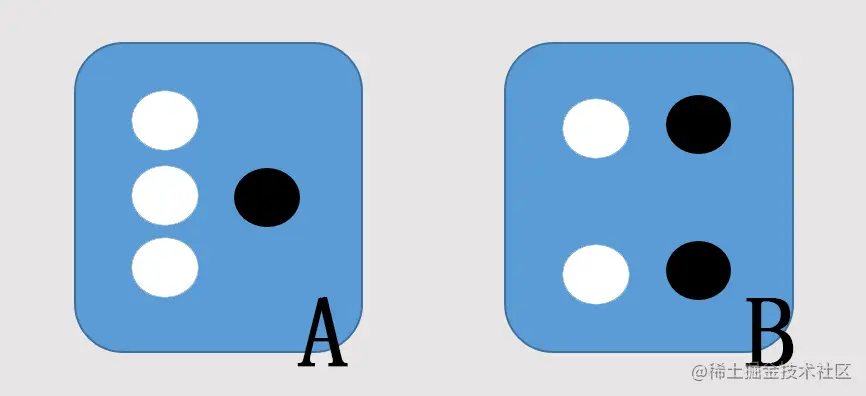
有两个外观看上去一模一样的密封箱子 A, B

A 箱中有 3 个白球和 1 个黑球

B 箱中有 2 个白球和 2 个黑球

P(w) = \frac{1}{2} \times \frac{3}{4} + \frac{1}{2} \times \frac{2}{4} = \frac{5}{8}

P(b) = \frac{1}{2} \times \frac{1}{4} + \frac{1}{2} \times \frac{2}{4} = \frac{3}{8}

这可以看作是随机摸一个球的先验分布，白色黑色的概率为先验概率

在计算过程中其实运用了全概率公式，枚举了选择两个箱子的情况

这里面认定了选择箱子A和箱子B的概率是1/2，这也是一种先验概率/先验分布

贝叶斯公式：

{%raw%}

\begin{array}{l} P(A|w) &= \frac{{P(w|A) \cdot P(A)}}{{P(w)}}\\ &= \frac{{\frac{3}{4} \cdot \frac{1}{2}}}{{\frac{5}{8}}} \\ &= \frac{3}{5} \end{array}

{%endraw%}

这个过程就是采样过后，对先验概率进行调整，得到后验概率。

先验概率、后验概率、似然函数概念与联系