【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（12）：相似形理论

海轰Pro
194 阅读8分钟

「这是我参与2022首次更文挑战的第16天，活动详情查看：2022首次更文挑战」。

@TOC

在这里插入图片描述

前言

Hello！小伙伴！ 非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～   自我介绍 ଘ(੭ˊᵕˋ)੭ 昵称：海轰 标签：程序猿｜C++选手｜学生 简介：因C语言结识编程，随后转入计算机专业，有幸拿过一些国奖、省奖...已保研。目前正在学习C++/Linux/Python 学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！   机器学习小白阶段 文章仅作为自己的学习笔记 用于知识体系建立以及复习 知其然 知其所以然！

往期文章

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（1）：集合与映射

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（2）：线性空间定义及其性质

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（3）：线性空间的基与坐标

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（4）：基变换与坐标变换

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（5）：线性子空间

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（6）：子空间的交与和

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（7）：欧氏空间

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（8）：标准正交基与Gram-Schmidt过程

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（9）：正交补与投影定理

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（10）：线性变换定义

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（11）：线性变换的矩阵表示

3.3 线性变换的最简矩阵表示-相似形理论

3.3.1 一般数域上矩阵相似最简形

定义3.9

设A,BA,B均为nn阶方阵，若存在nn阶可逆矩阵CC，使C−1AC=BC^{-1}AC=B

称AA与BB相似，记为A∼BA\sim B

定理3.3.1

nn维线性空间VV上的线性变换A\mathscr{A}在不同的基下的矩阵表示是相似的

反之，相似矩阵可以看做某一线性变换在不同基下的矩阵表示

证明

设ε1,ε2,...,εn\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n和ε1′,ε2′,...,εn′\boldsymbol\varepsilon^{'}_1,\boldsymbol\varepsilon^{'}_2,...,\boldsymbol\varepsilon^{'}_n分别是VV的两个基底

它们之间存在关系：

(\boldsymbol\varepsilon^{'}_1,\boldsymbol\varepsilon^{'}_2,...,\boldsymbol\varepsilon^{'}_n)=(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)C\tag{1}

设线性变换A\mathscr{A}在基ε1,ε2,...,εn\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n和ε1′,ε2′,...,εn′\boldsymbol\varepsilon^{'}_1,\boldsymbol\varepsilon^{'}_2,...,\boldsymbol\varepsilon^{'}_n下的矩阵表示分别为A、BA、B，有

\mathscr{A}(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)=(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)A\tag{2}

\mathscr{A}(\boldsymbol\varepsilon^{'}_1,\boldsymbol\varepsilon^{'}_2,...,\boldsymbol\varepsilon^{'}_n)=(\boldsymbol\varepsilon^{'}_1,\boldsymbol\varepsilon^{'}_2,...,\boldsymbol\varepsilon^{'}_n)B\tag{3}

将(1)式代入(3)式，得到

\mathscr{A}(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)C=(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)CB\tag{4}

等式右乘C−1C^{-1}，得

\mathscr{A}(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)=\mathscr{A}(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)CBC^{-1}\tag{5}

联合(2)式和(5)式，有

\mathscr{A}(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)=(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)A\\ \mathscr{A}(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)=(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)CBC^{-1} \end{cases}

得到

A=CBC−1或B=C−1ACA=CBC^{-1}\quad或\quad B=C^{-1}AC

即，AA与BB相似

相似矩阵的性质

  1. 反射性 ：A∼AA \sim A
  2. 对称性 ：若A∼BA\sim B，则B∼AB\sim A
  3. 传递性：若A∼B,B∼CA\sim B,B\sim C,则A∼CA\sim C
  4. 可加性：若B1=C−1A1C,B2=C−1A2CB_1=C^{-1}A_1C,B_2=C^{-1}A_2C，则B1+B2∼A1+A2B_1+B_2\sim A_1+A_2
  5. 可乘性：若B1=C−1A1C,B2=C−1A2CB_1=C^{-1}A_1C,B_2=C^{-1}A_2C，则B1B2∼A1A2B_1B_2\sim A_1A_2
  6. 数乘性：若A∼BA\sim B，则kA∼kBkA\sim kB
  7. 若A∼B,f(x)∈K[x]A\sim B,f(x) \in K[x]，则f(A)∼f(B)f(A)\sim f(B)

定义3.10

设A\mathscr{A}是数域KK上nn维线性空间VV的线性变换，若对于λ0∈K\lambda_0\in K，存在非零向量α∈V\alpha\in V，使得

Aα=λ0α\mathscr{A}\alpha=\lambda_0\alpha

则称λ0\lambda_0是A\mathscr{A}的特征值，α\alpha是A\mathscr{A}关于λ0\lambda_0的特征向量

定理3.3.2

nn级方阵AA能相似于对角阵Λ\Lambda的充分必要条件是AA有nn个线性无关的特征向量ρ1,...,ρn\rho_1,...,\rho_n

定理3.3.3

线性变换A\mathscr{A}能由对角矩阵表示Λ=[λ1..λn]\Lambda=\begin{bmatrix} \lambda_1 & & & \\ & . & & \\ & &. & \\ & & & \lambda_n\\ \end{bmatrix}的充分必要条件是A\mathscr{A}有nn个线性无关的特征向量ε1′,...,εn′\boldsymbol{\varepsilon_1^{'}},...,\boldsymbol{\varepsilon_n^{'}}

若A(ε1′,ε2′,...,εn′)=(ε1′,ε2′,...,εn′)[λ1λ2...λn]\mathscr{A}(\boldsymbol\varepsilon^{'}_1,\boldsymbol\varepsilon^{'}_2,...,\boldsymbol\varepsilon^{'}_n)=(\boldsymbol\varepsilon^{'}_1,\boldsymbol\varepsilon^{'}_2,...,\boldsymbol\varepsilon^{'}_n)\begin{bmatrix} \lambda_1 &&&&&\\ & \lambda_2 &&&&\\ && . &&&\\ &&& . &&\\ &&&& . & \\ &&&&& \lambda_n \end{bmatrix}

因为

A(ε1,ε2,...,εn)=(ε1,ε2,...,εn)A\mathscr{A}(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)=(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)A

且

P−1AP=Λ,P=(ρ1,ρ2,...,ρn)P^{-1}AP=\Lambda,P=(\rho_1,\rho_2,...,\rho_n)

得到

εi′=(ε1,ε2,...,εn)ρii=1,2,...,n\boldsymbol\varepsilon^{'}_i=(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)\rho_i\quad i=1,2,...,n

定义3.12

设A∈Kn×nA\in K^{n×n}，则

  • 矩阵λE−A\lambda E - A称为AA的特征矩阵
  • 方程∣λE−A∣=0|\lambda E - A|=0称为AA的特征方程
  • 多项式∣λE−A∣|\lambda E - A|叫AA的特征多项式，记为fA(λ)f_{A}(\lambda)，即fA(λ)=∣λE−A∣f_{A}(\lambda)=|\lambda E - A|
  • fA(λ)f_{A}(\lambda)的根就是AA的特征值或特征根

nn级方阵AA在复数域CC上一定有nn个特征根（重根按重数算）

求线性变换A\mathscr{A}的特征值和特征值向量

步骤一

任选线性空间VV中的一组基ε1,ε2,...,εn\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n，求出A\mathscr{A}在ε1,ε2,...,εn\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n的矩阵表示AA

步骤二

求出特征多项式fA(λ)=∣λE−A∣f_A(\lambda)=|\lambda E - A|在数域KK中的全部特征根λ1,...,λk\lambda_1,...,\lambda_k，得到A\mathscr{A}的特征值

步骤三

对于每一个特征根λi\lambda_i，求解线性方程组

(λiE−A)χ=0(\lambda_i E- A)\boldsymbol\chi=\boldsymbol0

若ρi1,ρi2,...,ρili\rho_{i1},\rho_{i2},...,\rho_{il_i}是上式的基础解系

则其为矩阵AA对应于λi\lambda_i的线性无关的特征向量

步骤四

εit′=(ε1,ε2,...,εn)ρitt=1,2,...,li\boldsymbol\varepsilon^{'}_{it}=(\boldsymbol\varepsilon_1,\boldsymbol\varepsilon_2,...,\boldsymbol\varepsilon_n)\rho_{it}\quad t=1,2,...,l_i就是线性变换A\mathscr{A}的对应于λi\lambda_i的线性无关的特征向量

步骤五

若ε11′,...ε1l1′,...εk1′,...,εklk′\boldsymbol\varepsilon^{'}_{11},...\boldsymbol\varepsilon^{'}_{1l_1},...\boldsymbol\varepsilon^{'}_{k1},...,\boldsymbol\varepsilon^{'}_{kl_k}是nn个线性无关的特征向量，那么它们可作VV的基，且A\mathscr{A}在此基下的矩阵表示是对角阵Λ\Lambda

\lambda_1 &&&&\\ & . &&&\\ && . &&\\ &&& . &\\ &&&& \lambda_k \end{bmatrix}_{n×n}$$ ### 定理3.3.4 相似矩阵有完全相同的特征值 ### 定理3.3.5 如果$\rho_1,...,\rho_m$是$A$的分别属于互不相同的特征值$\lambda_1,...,\lambda_m$的特征向量，则$\rho_1,...,\rho_m$线性无关 **推论** 若$n$级矩阵$A$有$n$个互不相同的特征值，则$A$可相似于对角阵 > 若$A$有重根，则需要进行更深层次的分析，用于判断是否可相似于对角阵 ### 定理3.3.6 设$\lambda_1,...,\lambda_k$是A的互不相同的特征值，$\rho_{11},...,\rho_{1r_{1}}$是$\lambda_1$对应的$r_1$个线性无关特征向量，.... ，$\rho_{k1},...,\rho_{kr_{k}}$是$\lambda_k$对应的$r_k$个线性无关的特征值向量，则$\rho_{11},...,\rho_{1r_1},...,\rho_{k1},...,\rho_{kr_k}$是线性无关的 ### 定理3.3.7 $\lambda_0$是$A$的一个$k$重特征值，则对应于$\lambda_0$的$A$的线性无关向量的最多个数$\leq k$ **推论** 一个矩阵$A$在复数域$C$上能化为对角阵的充要条件是对应于$A$的**每一个特征值的特征向量的线性无关最大个数等于该特征值的重根个数** ### 定理3.3.8 任意**实对称矩阵**一定相似于对角阵，且它的不同特征值对应的特征向量总是正交的 ## 3.3.2 复数域上矩阵相似最简型-若当形矩阵 ### 变量$\lambda$的多项式矩阵 以$\lambda$的多项式为元素的矩阵，如 $$A(\lambda)=\begin{bmatrix} a_{11}(\lambda) & . &. & a_{1n}(\lambda)\\ . & . & . & . \\ . & . & . & . \\ a_{m1}(\lambda) & . &. & a_{mn}(\lambda)\\ \end{bmatrix} \quad a(_{ij})(\lambda) \in K[\lambda]$$ 叫做多项式矩阵，又称$\lambda$-矩阵 --- 其中$K[\lambda]$表示系数是数域$K$上的多项式全体 $a_{ij}(\lambda)\in K[\lambda]$ 设$a_{ij}(\lambda)=a_n\lambda^n+a_{n-1}\lambda^{n-1}+...+a_1\lambda+a_0$ 若$a_n \neq 0$，称多项式$a_{ij}(\lambda)$的次数为$n$，记为$\vartheta\alpha_{ij}$ 若$a_n = 1$，称$a_{ij}(\lambda)$是首一多项式 ### 定义3.13 若$\lambda$-矩阵$A(\lambda)$中有一个$r(r\geq1)$级子式不恒为0，而所有的$r+1$级子式（存在的情况下）恒为0 则称$A(\lambda)$的秩为$r$，记为$rankA(\lambda)=r$，简记为$r(A)=r$ ### 定义3.14 设$A(\lambda)$是一个$n$级$\lambda$-方阵 若存在$n$级$\lambda$-方阵$B(\lambda)$，使得$A(\lambda)B(\lambda)=B(\lambda)A(\lambda)=E$ 则称$A(\lambda)$是可逆$\lambda$-矩阵，并称$B(\lambda)$是$A(\lambda)$的逆阵，记为$A^{-1}(\lambda)$ --- 若$A(\lambda)$可逆，则$A^{-1}(\lambda)$是惟一的 特别注意：在数字矩阵中，满秩矩阵就是可逆矩阵，但满秩的$\lambda$-矩阵未必可逆，比如$A(\lambda)=A=\begin{bmatrix} \lambda & 0\\ 0 & 1 \end{bmatrix}$ ### 定理3.3.9 一个$n$级$\lambda-$方阵$A(\lambda)$可逆的充分必要条件是行列式$|A(\lambda)|$为非零常数 ### 定义3.15：三种$\lambda$-矩阵的初等变换 （1）互换$A(\lambda)$的$i,j$两行（列），相当于左（右）乘以初等$\lambda$-矩阵 ![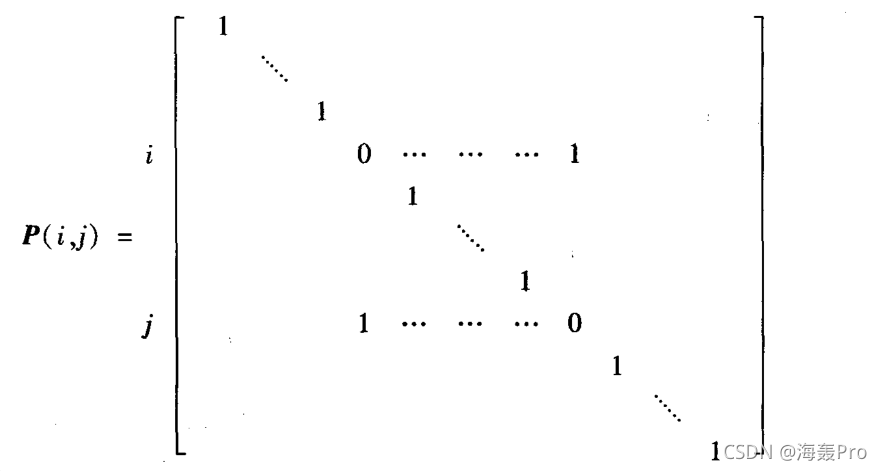在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/1faa91cc4922461ea9dfe177adbb4e97~tplv-k3u1fbpfcp-zoom-1.image) （2）$A(\lambda)$的第$i$行（列）扩大$k$倍（$k\neq 0$），相当于左（右）乘以初等$\lambda$-矩阵 ![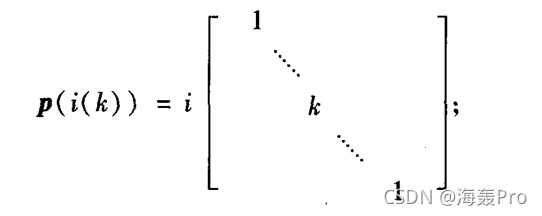在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/b878728db8cb45caa396af05492fbb3c~tplv-k3u1fbpfcp-zoom-1.image) （3）把$A(\lambda)$的第$i$行的$\varphi(\lambda)$倍（是一个多项式）加到第$j$行上，相当于左乘以初等$\lambda$-矩阵 ![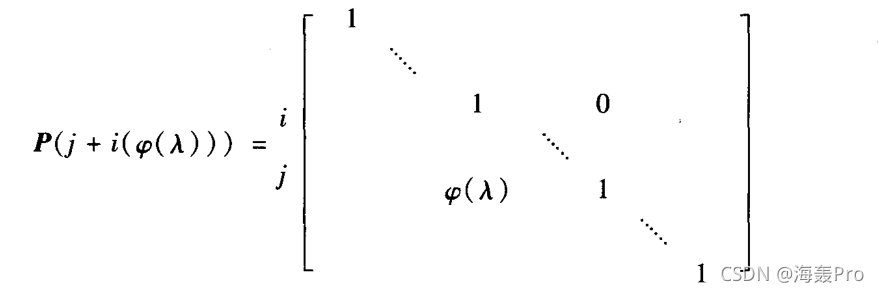在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/9f5182e49bcd4133b037d9563b676316~tplv-k3u1fbpfcp-zoom-1.image) --- 若$A(\lambda)$经过有限次初等变换变为$B(\lambda)$，称为$A(\lambda)$与$B(\lambda)$等价，记作 $$A(\lambda)\stackrel{\sim}{=}B(\lambda)$$ 等价关系满足 - 自反性：$A(\lambda)\stackrel{\sim}{=}A(\lambda)$ - 对称性：若$A(\lambda)\stackrel{\sim}{=}B(\lambda)$则$B(\lambda)\stackrel{\sim}{=}A(\lambda)$ - 传递性：若$A(\lambda)\stackrel{\sim}{=}B(\lambda)$，$B(\lambda)\stackrel{\sim}{=}C(\lambda)$，则$A(\lambda)\stackrel{\sim}{=}C(\lambda)$ ### 定理3.3.10 两个$m×n$阶的$\lambda$-矩阵$A(\lambda),B(\lambda)$等价的充分必要条件是存在可逆$m$阶$P(\lambda)$阵及$n$阶$Q(\lambda)$阵，使得 $$P(\lambda)A(\lambda)Q(\lambda)=B(\lambda)$$ ### 定理3.3.11 设$A,B$是两个数字矩阵，则$A\sim B$的充分必要条件是$\lambda E - A\stackrel{\sim}{=}\lambda E - B$ ### 定理3.3.12：smith标准形 任意一个秩为$r$的$m×n$阶$\lambda$-矩阵$A(\lambda)$都等价于一个对角形$\lambda$-矩阵 ![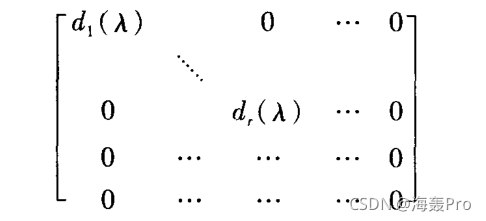在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/b3b7ce6c304a42e082af3f5e4f0cf32e~tplv-k3u1fbpfcp-zoom-1.image) 其中$d_i(\lambda)(i=1,...,r)$都是**首一多项式**，且$d_i(\lambda)|d_{i+1}(\lambda)$，此对角形矩阵叫$A(\lambda)$的smith标准形 > $d_i(\lambda)|d_{i+1}(\lambda)$表示存在多项式$g(\lambda)$，使得$d_{i+1}(\lambda)=d_i(\lambda)g(\lambda)$ > 简单的理解，就是$d_{i+1}$可以整除$d_i$ ---- **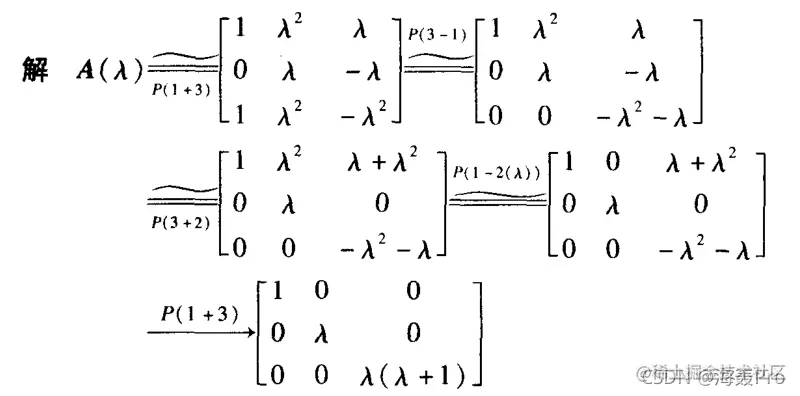例题**：利用初等变换化$\lambda-$矩阵 $$A(\lambda)=\begin{bmatrix} 1-\lambda & \lambda^2 & \lambda\\ \lambda & \lambda & -\lambda\\ 1 + \lambda^2 & \lambda^2 & -\lambda^2 \end{bmatrix}

为Smith标准形

在这里插入图片描述

定义3.16

设rankA(λ)=r(r≥1)rankA(\lambda)=r(r\geq1)，则对正整数k(1≤k≤r)k(1\leq k \leq r)，A(λ)A(\lambda)中必有非0点kk阶子式

A(λ)A(\lambda)的全部kk阶子式的最高公因式（首1多项式）记为Dk(λ)D_k(\lambda)，称之为A(λ)A(\lambda)的kk阶行列式因子

当r≥1r \geq 1时，A(λ)A(\lambda)有rr个行列式因子D1(λ),D2(λ),...,Dr(λ)D_1(\lambda),D_2(\lambda),...,D_r(\lambda)

定理3.3.13

若A(λ)=∼B(λ)A(\lambda)\stackrel{\sim}{=}B(\lambda)，则A(λ)A(\lambda)与B(λ)B(\lambda)有相同的秩及各级行列式因子

A(λ)A(\lambda)经过有限次初等变换成smith标准形B(λ)B(\lambda)，即

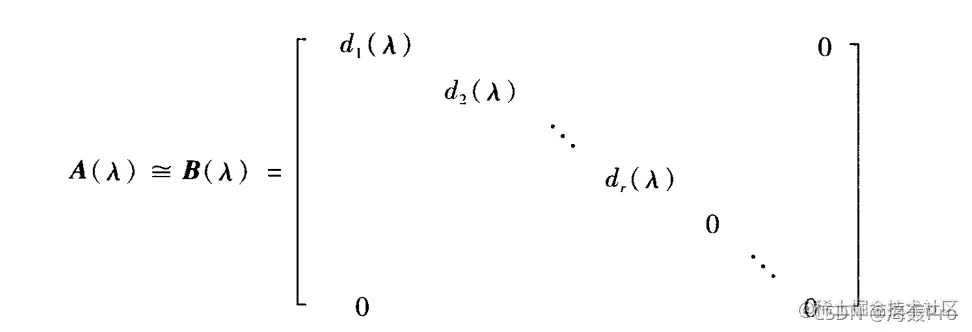
在这里插入图片描述

因为d1(λ),...,dr(λ)d_1(\lambda),...,d_r(\lambda)皆为多项式，di(λ)∣di+1(λ)i=1,2,...,r−1d_i(\lambda) | d_{i+1}(\lambda) \quad i = 1,2,...,r-1

那么

D1(λ)=d1(λ)D_1(\lambda)=d_1(\lambda)

D2(λ)=d1(λ)d2(λ)D_2(\lambda)=d_1(\lambda)d_2(\lambda)

............

Dr(λ)=d1(λ)...dr(λ)D_r(\lambda)=d_1(\lambda)...d_r(\lambda)

即

d1(λ)=D1(λ)d_1(\lambda)=D_1(\lambda)

d2(λ)=D2(λ)D1(λ)d_2(\lambda)=\frac{D_2(\lambda)}{D_1(\lambda)}

............

dr(λ)=Dr(λ)Dr−1(λ)d_r(\lambda)=\frac{D_r(\lambda)}{D_{r-1}(\lambda)}

其中d1(λ),d2(λ),...,dr(λ)d_1(\lambda),d_2(\lambda),...,d_r(\lambda)称为A(λ)A(\lambda)的不变因子

因此A(λ)A(\lambda)的smith标准形是惟一的

例题

设A(λ)=[1−λλ2λλλ−λ1+λ2λ2−λ2]A(\lambda)=\begin{bmatrix} 1-\lambda & \lambda^2 & \lambda\\ \lambda & \lambda & -\lambda\\ 1+ \lambda^2 & \lambda^2 & -\lambda^2 \end{bmatrix}，求A(λ)A(\lambda)的Smith标准形

解答

观察A(λ)A(\lambda)，可以发现

a11(λ)a_{11}(\lambda)与a21(λ)a_{21}(\lambda)互素，故D1(λ)=1D_1(\lambda)=1

又因为

1-\lambda & \lambda^2\\ \lambda & \lambda \end{vmatrix}=\lambda(1-\lambda-\lambda^2),\begin{vmatrix} \lambda^2 & \lambda\\ \lambda & -\lambda \end{vmatrix}=\lambda^2(1-\lambda)$$ 所以$D_2(\lambda)=\lambda$ $D_3(\lambda)=|A(\lambda)|=\lambda^2(\lambda+1)$ 综上，可以得到 $d_1(\lambda)=D_1(\lambda)=1$ $d_2(\lambda)=\frac{D_2(\lambda)}{D_1(\lambda)}=\lambda$ $d_3(\lambda)=\frac{D_3(\lambda)}{D_2(\lambda)}=\lambda(\lambda+1)$ 故，$A(\lambda)$的Smith标准形为 $$\begin{bmatrix} 1 & & \\ & \lambda & \\ & & \lambda(\lambda+1) \end{bmatrix}

定义3.17

设A(λ)A(\lambda)的不变因子d1(λ),d2(λ),...,dr(λ)d_1(\lambda),d_2(\lambda),...,d_r(\lambda)

这些不变因子在复数域分解为一次因式方幂

\quad \\ d_2(\lambda) = (\lambda - \lambda_1)^{l_{11}} (\lambda - \lambda_2)^{l_{22}}... (\lambda - \lambda_t)^{l_{2t}}\\ \quad \\ ............................................................\\ d_r(\lambda) = (\lambda - \lambda_1)^{l_{r1}} (\lambda - \lambda_2)^{l_{r2}}... (\lambda - \lambda_t)^{l_{rt}}$$ 其中$l_{ij}\geq0\quad(i = 1,...,r;j = 1,2,...,t)$ 称$l_{ij}>0$的所有$(\lambda-\lambda_j)^{l_{ij}}$为$A(\lambda)$的<font color="red">初等因子</font> --- 对于数字矩阵$A$，$\lambda E - A$的初等因子就称为$A$的初等因子 $A(\lambda)$的初等因子有可能有相同的 注：称$n$阶矩阵$A$的特征矩阵$\lambda E - A$的初等因子为矩阵$A$的初等因子 ### 定理3.3.14 $A(\lambda)$与$B(\lambda)$都是$m×n$阶$\lambda$-矩阵，则以下命题等价 - $A(\lambda)\stackrel{\sim}{=}B(\lambda)$ - $A(\lambda),B(\lambda)$有相同的smith标准形 - $A(\lambda),B(\lambda)$有相同的各级行列式因子 - $A(\lambda),B(\lambda)$有相同的不变因子 - $A(\lambda),B(\lambda)$有相同的秩及初等因子 - 存在可逆矩阵$P(\lambda),Q(\lambda)$,使得$P(\lambda)A(\lambda)Q(\lambda)=B(\lambda)$ ![在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/14a958aed8624cb09f0a9f65395d30ab~tplv-k3u1fbpfcp-zoom-1.image) ### 定义3.18 形式为 ![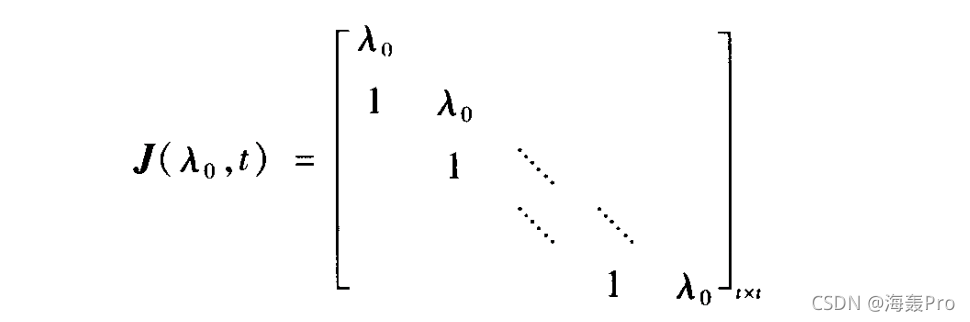在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/f55160e012c1403eac1956397c2f6a72~tplv-k3u1fbpfcp-zoom-1.image) 的矩阵称为<font color="red">若当块</font>，其中$\lambda_0$为复数 --- 由若干个若当块组成的准对角矩阵称为<font color="red">若当形矩阵</font> ![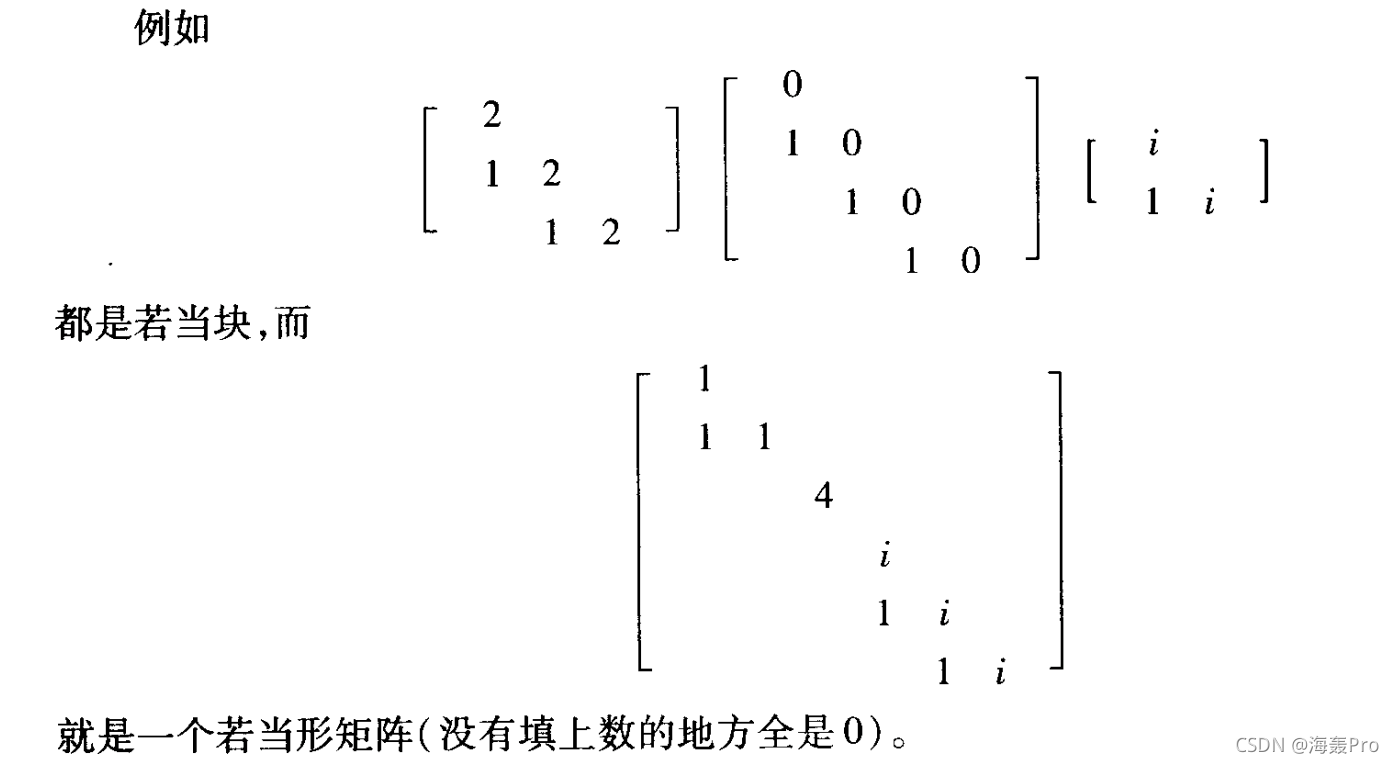在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/42763397936d4757889f09bca8bb3919~tplv-k3u1fbpfcp-zoom-1.image) > 一阶若当块就是一阶矩阵，因此若当形矩阵包括对角阵 ### 定理3.3.15 若$A(\lambda)$呈分块对角形 ![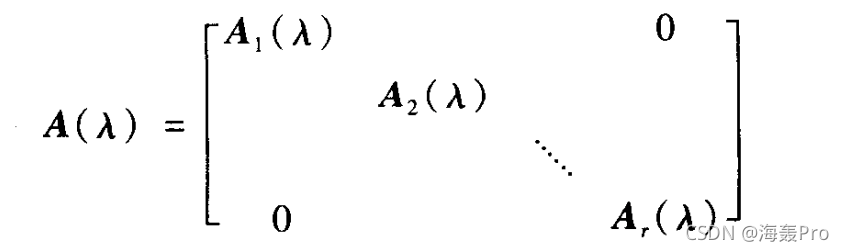在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/a63e03f82ca041e896bd91583e9f9f08~tplv-k3u1fbpfcp-zoom-1.image) $A_1(\lambda),...,A_r(\lambda)$都是$\lambda$-矩阵，则$A_1(\lambda),...,A_r(\lambda)$的全部初等因子就是$A(\lambda)$的全部初等因子 --- ### 若当块$J(\lambda_0,t)$的初等因子 ![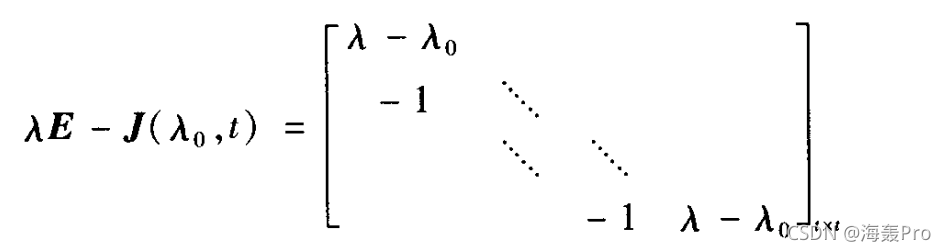在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/a62def1583c540fbb402f49d21cc4d26~tplv-k3u1fbpfcp-zoom-1.image) 若当块$J(\lambda_0,t)$的初等因子就是$(\lambda-\lambda_0)^t$ > 给出一个一次因式幂$(\lambda-\lambda_0)^t$，可以惟一写出一个若当块$J(\lambda_0,t)$,使得$J(\lambda_0,t)$的初等因子就是$(\lambda-\lambda_0)^{t}$ ### 若当形矩阵的初等因子 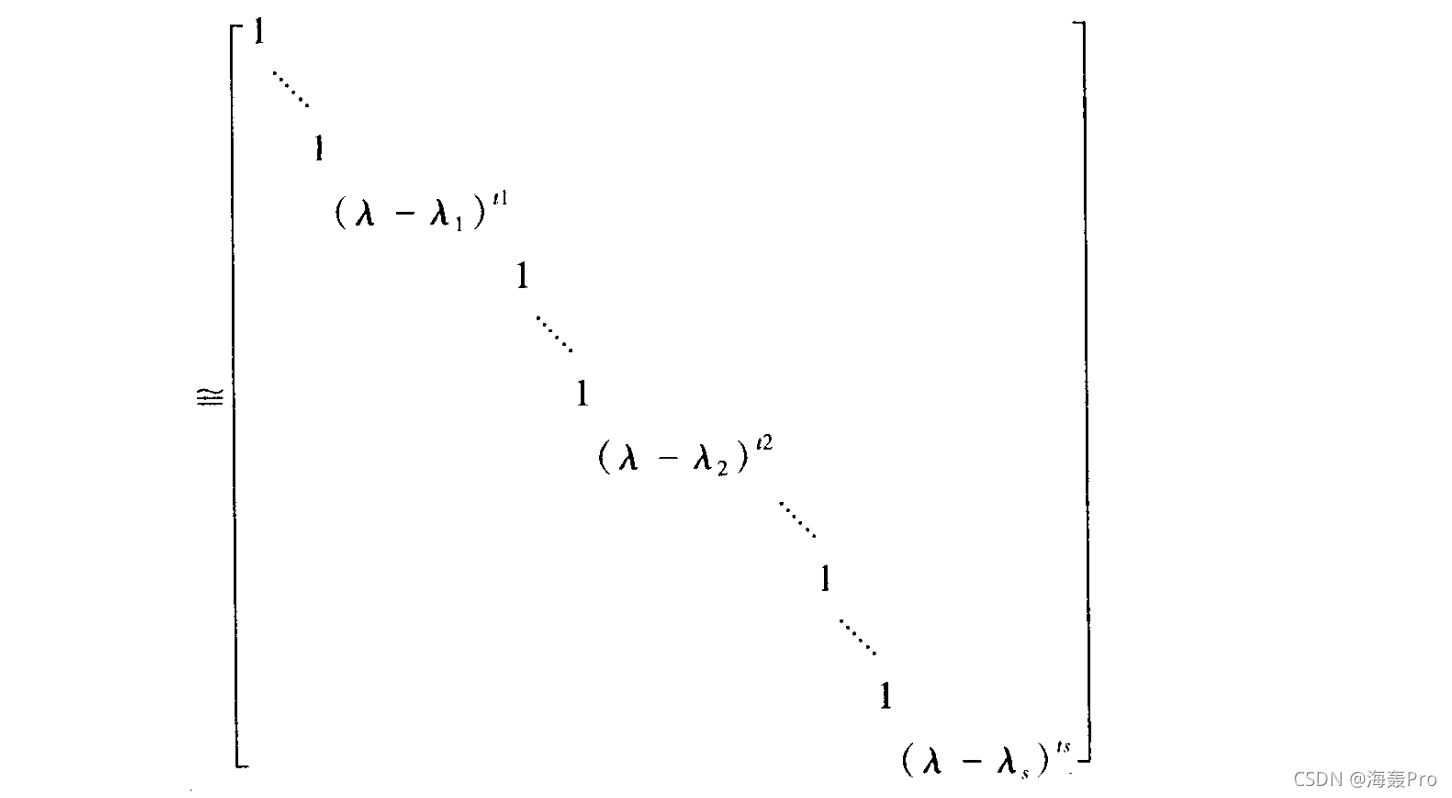设若当形矩阵$J$ ![在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/6796bf416e7844d7a3f600f8e7cbbac3~tplv-k3u1fbpfcp-zoom-1.image) 其中$J_i=J_i(\lambda_i,t_i)\quad(i = 1,2,...,s)$ 那么其特征矩阵$\lambda E - J$ ![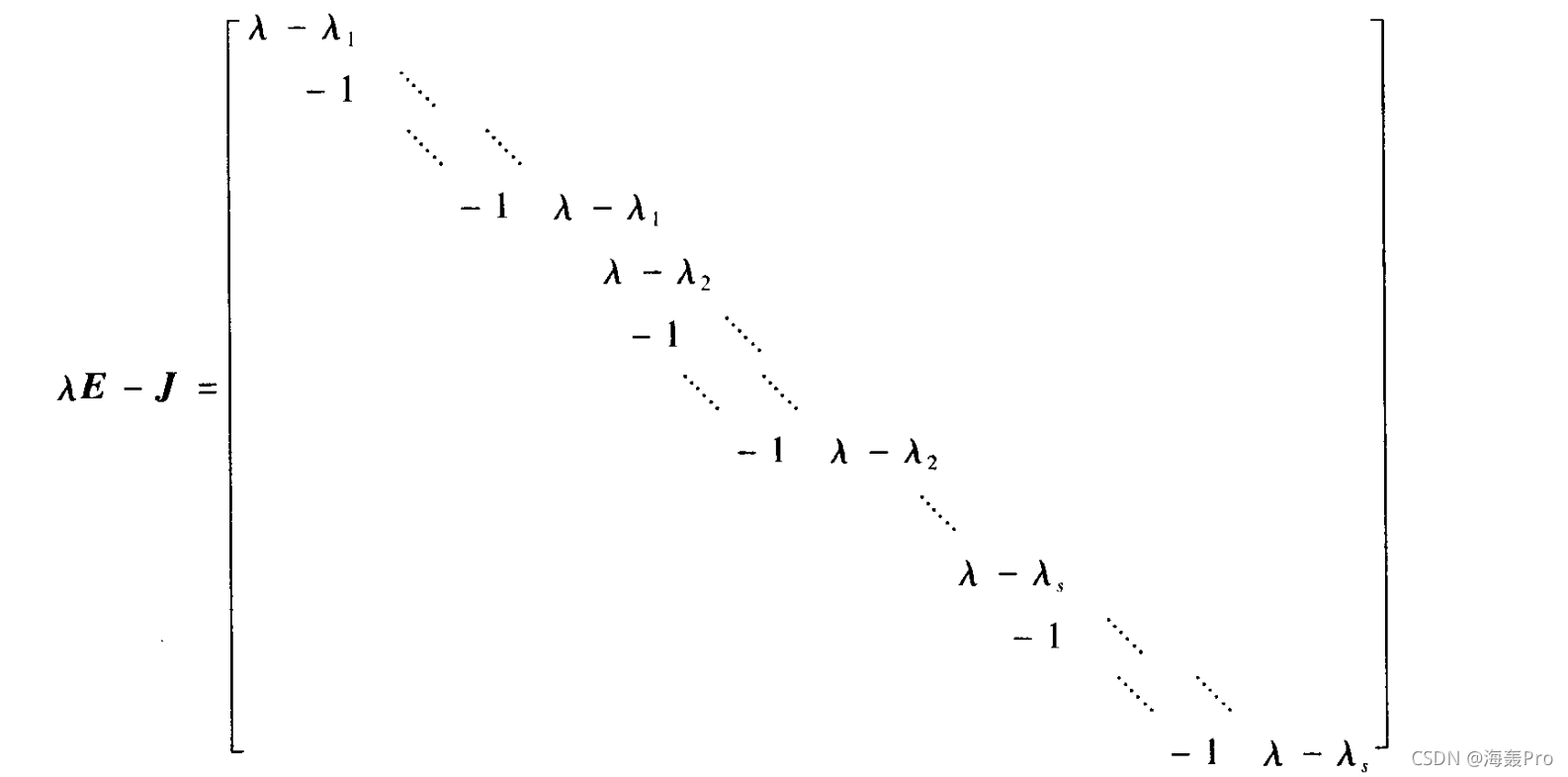在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/4625f853a3274fe4985ab1ca5a31b7ce~tplv-k3u1fbpfcp-zoom-1.image)![在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/f35f7c306688468491c3420eb0a159bd~tplv-k3u1fbpfcp-zoom-1.image) 由定理3.3.15可知$J$的全部初等因子就是$(\lambda-\lambda_1)^{t1},...,(\lambda-\lambda_s)^{ts}$ ### 定理3.3.16 复数域上任意一个$n$级方阵$A$，总是可以相似于一个若当形矩阵$J$，若不计较若当块的顺序，$J$还是唯一的 # 结语 说明： - 参考于 课本《矩阵理论》 - 配合书中概念讲解 结合了自己的一些理解及思考 文章仅作为学习笔记，记录从0到1的一个过程 希望对您有一点点帮助，如有错误欢迎小伙伴指正 ![在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/da0cd6393c7b4995901b5c344e87ce2e~tplv-k3u1fbpfcp-zoom-1.image)
avatar
文章
阅读
粉丝