「这是我参与2022首次更文挑战的第12天，活动详情查看：2022首次更文挑战」。

@TOC

前言

Hello！小伙伴！ 非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～   自我介绍 ଘ(੭ˊᵕˋ)੭ 昵称：海轰 标签：程序猿｜C++选手｜学生 简介：因C语言结识编程，随后转入计算机专业，有幸拿过一些国奖、省奖...已保研。目前正在学习C++/Linux/Python 学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！   机器学习小白阶段 文章仅作为自己的学习笔记 用于知识体系建立以及复习 知其然 知其所以然！

往期文章

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（1）：集合与映射

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（2）：线性空间定义及其性质

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（3）：线性空间的基与坐标

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（4）：基变换与坐标变换

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（5）：线性子空间

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（6）：子空间的交与和

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（7）：欧氏空间

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（8）：标准正交基与Gram-Schmidt过程

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（9）：正交补与投影定理

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（10）：线性变换定义

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（11）：线性变换的矩阵表示

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（12）：相似形理论

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（13）：Hamliton-Cayley定理、最小多项式

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（14）：向量范数及其性质

【机器学习｜数学基础】Mathematics for Machine Learning系列之矩阵理论（15）：矩阵的范数

5.1 向量和矩阵的极限

5.1.1 向量序列极限

定义5.1

设给定$n$维向量空间$C^n$中的向量序列$\{\boldsymbol\chi^{(k)}\}$，其中

$\boldsymbol\chi^{(k)}=(\xi_1^{(k)},\xi_2^{(k)},...,\xi_n^{(k)})\quad k=1,2,3,...$

如果每一个分量$\xi_i^{(k)}$当$k\rightarrow\infty$时，都有极限$\xi_i$，即

$\lim_{k\rightarrow\infty}\xi_i^{(k)}=\xi_i\quad i=1,2,...,n$

记$\boldsymbol\chi=(\xi_1,\xi_2,...,\xi_n)$

则称向量序列$\{\boldsymbol\chi^{(k)}\}$有极限或称$\{\boldsymbol\chi^{(k)}\}$收敛于$\boldsymbol\chi$

简称$\{\boldsymbol\chi^{(k)}\}$收敛，记为

$\lim_{k\rightarrow\infty}\boldsymbol\chi^{(k)}=\boldsymbol\chi或\boldsymbol\chi^{(k)}\rightarrow\boldsymbol\chi$

向量序列$\{\boldsymbol\chi^{(k)}\}$含有很多项 简单的理解：由$\boldsymbol\chi^{(1)}、\boldsymbol\chi^{(2)}、\boldsymbol\chi^{(3)}...\boldsymbol\chi^{(k)}$组成 然后随着$k$的增大，逐渐趋近于向量$\boldsymbol\chi$

---

由向量序列极限定义易知，向量序列$\{\boldsymbol\chi^{(k)}\}$收敛于$\boldsymbol\chi$的充分必要条件

• $\{\boldsymbol\chi^{(k)}-\boldsymbol\chi\}$收敛于零向量

或者是

• 对任意一种向量范数$||\cdot||$，序列$||\{\boldsymbol\chi^{(k)}-\boldsymbol\chi\}||$收敛于零

5.1.2 方阵序列极限

定义5.2

对于复方阵序列$\{A_k\}$，其中

若在$k\rightarrow\infty$时，$n^2$个复数序列$\{a_{ij}^{(k)}\}$都分别收敛于$a_{ij}$，即

$\lim_{k\rightarrow\infty}a_{ij}^{(k)}=a_{ij}\quad(i,j = 1,2,...,n)$

则称$A$是$\{A_k\}$在$k\rightarrow\infty$的极限，记作

$\lim_{k\rightarrow\infty}A_k=A$

即

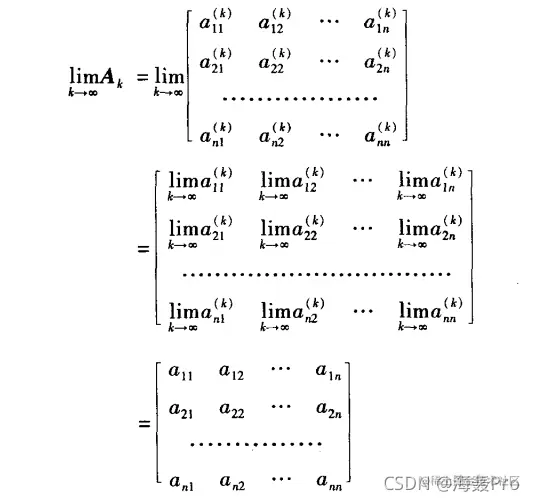若$k\rightarrow\infty$时，$\{A_k\}$不收敛，则称方阵序列$\{A_k\}$是发散的

只要$\{A_k\}$中有一个元素$a_{ij}^{(k)}$在$k\rightarrow\infty$不收敛，则$\{A_k\}$一定是不收敛的 只有$\{A_k\}$中所有元素$a_{ij}^{(k)}$在$k\rightarrow\infty$都收敛，则$\{A_k\}$是收敛的

定理5.1.1

$C^{n×n}$中的矩阵序列$\{A_k\}$收敛于方阵$A$的充分必要条件是：对任意一种方阵范数$||\cdot||$，序列$\{||A_k-A||\}$都收敛于0

$\{A_k\}$是矩阵序列，具体是$A_1,A_2,A_3,...,A_k$ $\{||A_k||\}$是一般的数列，具体是$||A_1||,||A_2||,...,||A_k||$,因为$||A_k||$表示的只是一项，所以 $\{||A_k||\}$则是一般的数列

$C^{n×n}$中收敛的方阵序列的性质

（1）若$\lim_{k\rightarrow\infty}A_k=A$，则对$C^{n×n}$中任意方阵范数$||\cdot||$，$||A_k||$有界

（2）若$\lim_{k\rightarrow\infty}A_k=A,\lim_{k\rightarrow\infty}B_k=B$，且$\lim_{k\rightarrow\infty}a_k=a,\lim_{k\rightarrow\infty}b_k=b$，$\{a_k\},\{b_k\}$是数列，则

$\lim_{k\rightarrow\infty}(a_kA_k+b_kB_k)=aA+bB$

（3）若$\lim_{k\rightarrow\infty}A_k=A,\lim_{k\rightarrow\infty}B_k=B$，则

$\lim_{k\rightarrow\infty}A_kB_k=\lim_{k\rightarrow\infty}A_k\cdot\lim_{k\rightarrow\infty}B_k=AB$

（4）$\lim_{k\rightarrow\infty}A_k=A$，且$A_k^{-1}$及$A^{-1}$存在，则

$\lim_{k\rightarrow\infty}A_k^{-1}=A^{-1}$

Jordan块的正整数次幂

设

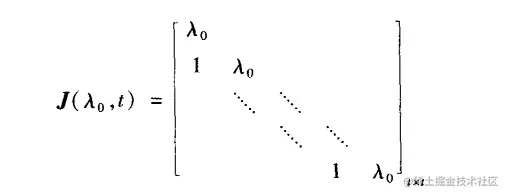是$t$阶Jordan块，并记$t$阶矩阵

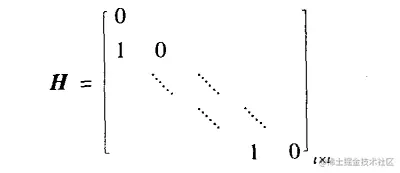则有

$J(\lambda_0,t)=\lambda_0 E + H\quad(E是t阶单位矩阵)$

由于

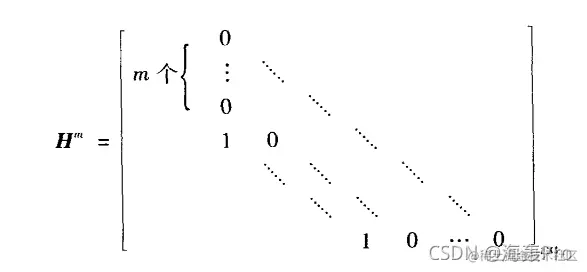及$H^t=0$,便有

$J^k(\lambda_0,t)=(\lambda_0 E + H)^k$

---

同理，对数值变量$x$，由

$J(\lambda_0,t)x=\lambda_0xE+xH$

可得

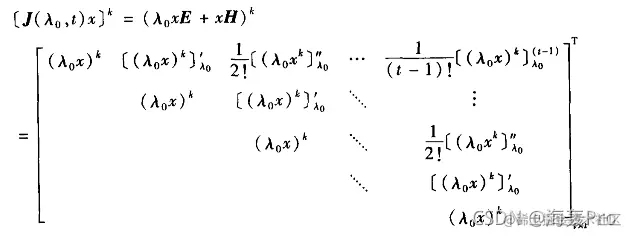
定理5.1.2

矩阵$A\in C^{n×n}$的方幂$E,A,A^2,...,A^k,...$所构成的矩阵序列$\{A^k\}$收敛于零矩阵的充分必要条件是$A$的特征值的模都小于1

命题

设$||A||_a$是相容于向量范数$||\boldsymbol\chi||_a$的方阵范数，则$\rho(A)\leq||A||_a$

定理5.1.3

$A^{k}\rightarrow0$的充分必要条件是至少存在一种方阵范数$||\cdot||$，使$||A||<1$

结语

说明：

• 参考于 课本《矩阵理论》
• 配合书中概念讲解 结合了自己的一些理解及思考

文章仅作为学习笔记，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正