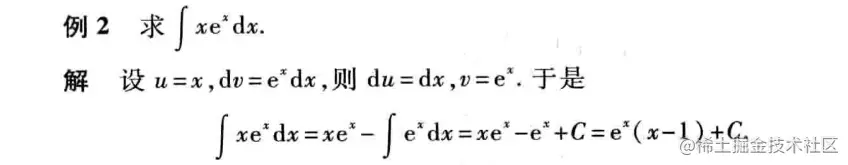「这是我参与2022首次更文挑战的第9天，活动详情查看：2022首次更文挑战」。

前言

很长一段时间没有接触高数了（大一学后就没有咋再学过），很多知识点都忘记的差不多了

最近学习需要用到以前的一些知识点，所以才编写这篇文章用以回忆、记录一下

基本积分表

$\int kdx=kx+C(k是常数)$

$\int x^{u}dx=\frac{x^{u+1}}{u+1}+C(u\neq -1)$

$\int \frac{dx}{x^3}=\int x^{-3}dx=\frac{x^{-3+1}}{-3+1}dx=-2x^{-2}+C$ $\int x^2\sqrt{x}dx=\int x^{\frac{5}{2}}dx=\frac{x^{\frac{5}{2}+1}}{\frac{5}{2}+1}=\frac{2}{7}x^{\frac{7}{2}}$

$\int\frac{1}{x}dx=\ln(|x|)+C$

$\int \frac{1}{1+x^2}dx=\arctan x + C$

$\int \frac{1}{\sqrt{1-x^2}}dx=\arcsin x + C$

$\int \cos x dx = \sin x + C$

$\int \sin x dx = -\cos x + C$

$\int \frac{1}{\cos^2x}dx=\int \sec^2 xdx = \tan x + C$

$\int \frac{1}{\sin^2x}dx = \int \csc^2 x dx = - \cot x + C$

$\int \sec x \tan x dx= \sec x + C$

$\int \csc x \cot x dx=-\csc x + C$

$\int e^x dx = e^x + C$

$\int a^x dx=\frac{a^x}{\ln a} + C$

不定积分的性质

性质1

设函数$f(x)$及$g(x)$的原函数存在，则

$\int [f(x)+g(x)]dx=\int f(x)dx + \int g(x)dx$

性质2

设函数$f(x)$的原函数存在，$k$为非零常数，则

$\int k f(x) dx = k \int f(x) dx$

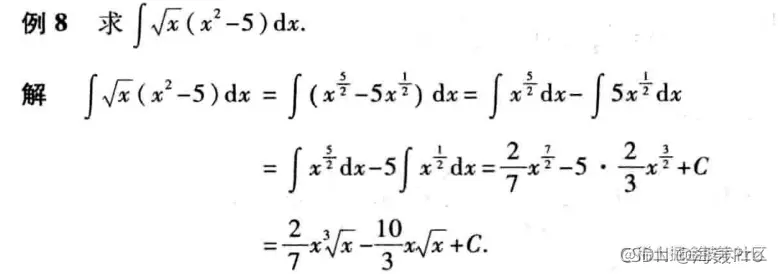
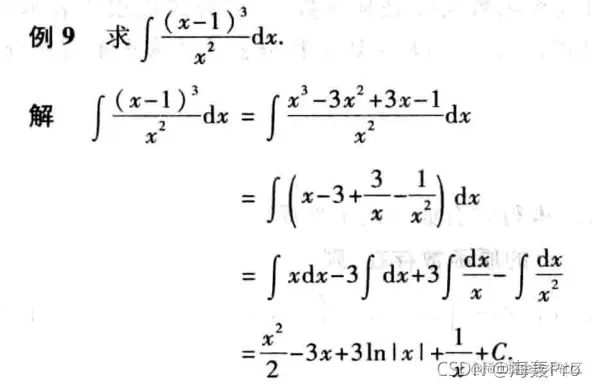
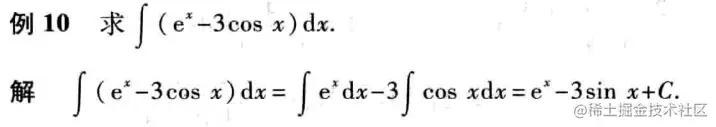
补充公式

\sin(2\alpha)=2\sin(\alpha)\cos(\beta)\tag{1}

$\sin(2\alpha)=\sin(\alpha+\alpha)=\sin(\alpha)\cos(\alpha)+\cos(\alpha)\sin(\alpha)=2\sin(\alpha)\cos(\beta)$

\cos(2\alpha)=2\cos^2(\alpha)-1=1-2\sin^2(\alpha)\tag{2}

$\cos(2\alpha)=\cos(\alpha+\alpha)=\cos(\alpha)\cos(\alpha)-\sin(\alpha)\sin(\alpha)=\cos^2(\alpha)-\sin^2(\alpha)=2\cos^2(\alpha)-1=1-2\sin^2(\alpha)$

\tan(2\alpha)=\frac{2\tan(\alpha)}{1-\tan^2(\alpha)}\tag{3}

换元积分法

第一类换元法

定理1

设$f(u)$具有原函数，$u=\varphi(u)$可导，则有换元公式

$\int f[\varphi(x)]\varphi^2(x)dx=[\int f(u)du]_{u= \varphi(x)}$

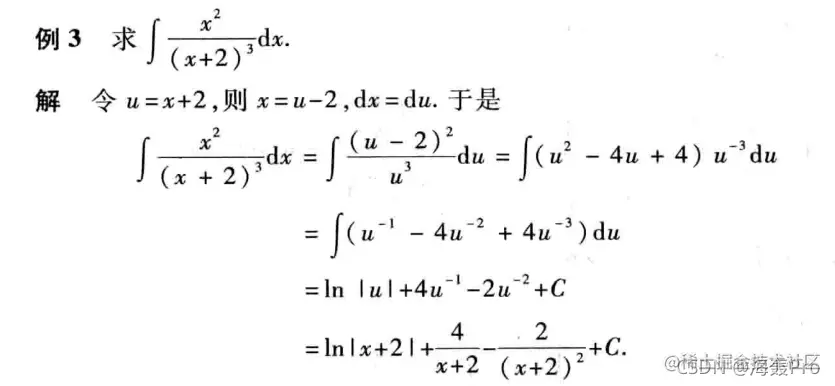
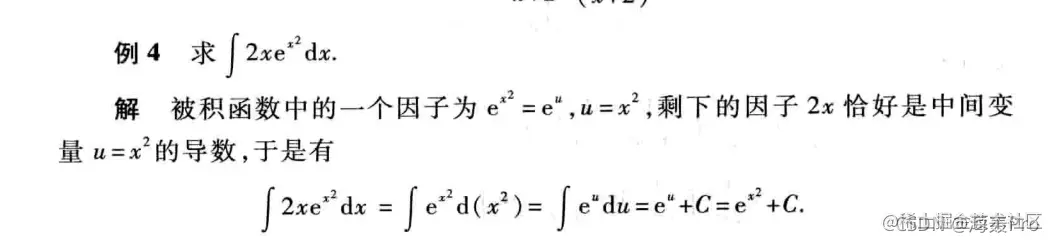
第二类换元法

分部积分法