SVM 的推导「这是我参与2022首次更文挑战的第8天，活动详情查看：2022首次更文挑战」。概述考虑一个分类任务

「这是我参与2022首次更文挑战的第8天，活动详情查看：2022首次更文挑战」。

SVM（Support Vector Machine，支持向量机）是一个线性分类器，是最经典的分类算法，其核心目标就是找到最大间隔超平面。本文记录SVM的推导过程。

概述

SVM就是一个分类器，只是相对于传统的线性分类器，它添加了一个支持向量的概念。

考虑一个分类任务

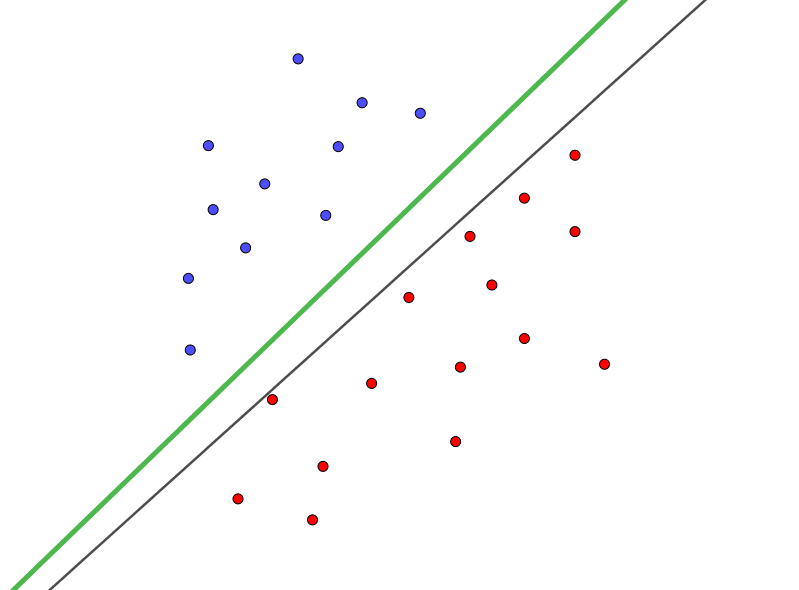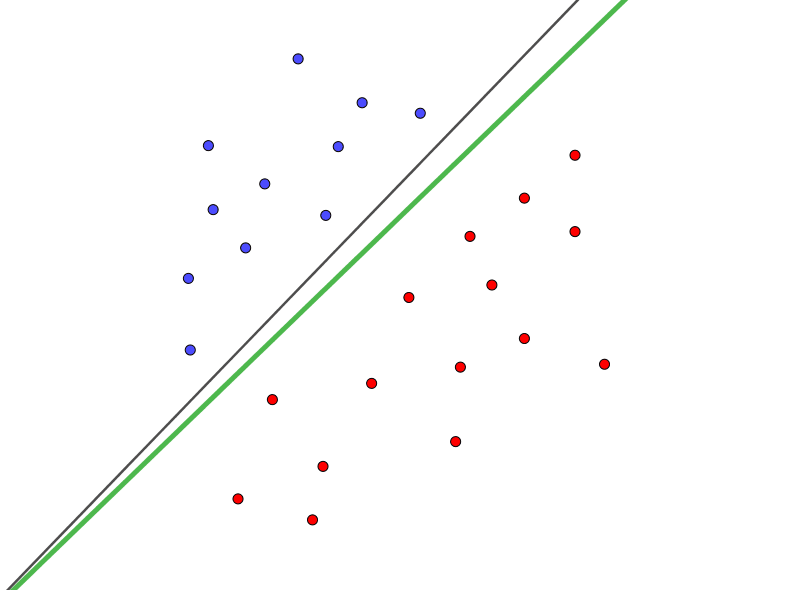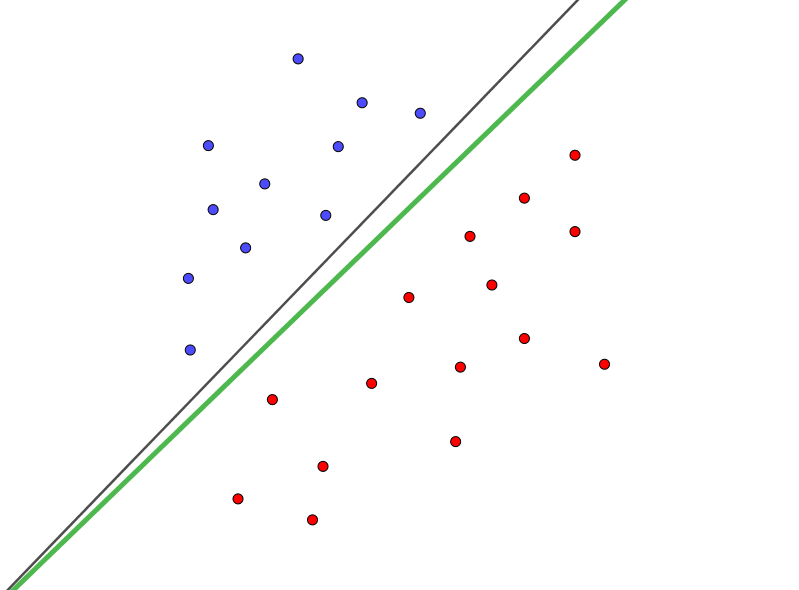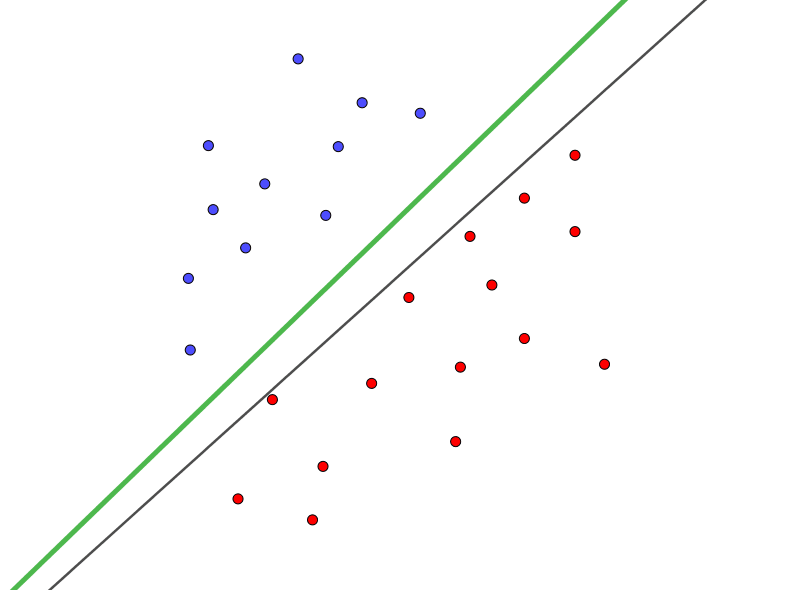
从图片上解释，对于一组数据，SVM在使用直线的同时要求数据点距离这条直线的最小距离最大，也就是说分类器和数据之间要有足够大的“间隔”。这样做的好处是很明显的，越大的“间隔”代表了更大的转圜空间，在得到新的数据之后更容易将其正确分类。

而SVM的工作就是求解这个最大间隔，也就是最优化问题。对于线性可分的数据，可以直接套用线性规划的知识进行推导，但如果数据线性不可分，就需要核函数进行数据升维，进行超平面分类。

目标函数

SVM是一个线性分类器，SVM的目标就是找到最大间隔超平面。

定义任意的超平面函数为：

\bf{w}^{T} \bf{x}+b=0

二维空间点 $(x,y)$ 到直线 $Ax+By+C=0$ 的距离为：

{% raw %}

\frac{|A x+B y+C|}{\sqrt{A^{2}+B^{2}}}

{% endraw %}

扩展到 $k$ 维空间后，点 $X=(x_1,x_2,\dots,x_k)$ 到超平面 $w^{T} x+b=0$ 距离为：

\frac{\left|\bf{w}^{T} \bf{x}+b\right|}{\|\bf{w}\|}

其中：

\|\bf{w}\|=\sqrt{w_{1}^{2}+\ldots w_{n}^{2}}

我们希望这个超平面可以区分不同两类数据特征，这个分类决策函数就是：

f(x)=\operatorname{sign}\left(\bf{w}^T\bf{x}+b\right)

我们的数据为{% raw %} $({{\bf{x}}_i},{y_i}),i \in \{ 1,2, \ldots ,n\},y_i \in \{1,-1\}$ {% endraw %}，定义点{% raw %} $({{\bf{x}}_i},{y_i})$ {% endraw %}到超平面的函数距离{% raw %} $\hat{\gamma}_{i}$ {% endraw %}：

{% raw %}

\hat{\gamma}_{i}=y_{i}\left(\bf{w} \cdot \bf{x}_{i}+b\right)

{% endraw %}

而我们的目标是找到可以最大化数据到点几何距离的超平面，将几何距离用 ${\gamma}_{i}$ 表示，为：

{% raw %}

\gamma_{i}=|\frac{\bf{w}}{\|\bf{w}\|} \cdot \bf{x}_{i}+\frac{b}{\|\bf{w}\|}|=\frac{|\bf{w}^T\bf{x}_i+b|}{\|\bf{w}\|}=\frac{y_{i}\left(\bf{w} \cdot \bf{x}_{i}+b\right)}{\|\bf{w}\|}=\frac{\hat{\gamma}_{i}}{\|\bf{w}\|}

{% endraw %}

因此优化函数为：

{% raw %}

\begin{array}{*{20}{l}} {\mathop {\max }\limits_{{\bf{w}},b} }&\gamma \\ {{\rm{ s}}{\rm{.t}}{\rm{. }}}&{{y_i}\left( {\frac{{\bf{w}}}{{{||\bf{w}||}}} \cdot {x_i} + \frac{b}{{{||\bf{w}||}}}} \right) \ge \gamma ,\quad i = 1,2, \cdots ,n} \end{array}

{% endraw %}

根据已有结论可以将优化函数转化为：

{% raw %}

\begin{array}{*{20}{l}} {\mathop {\max }\limits_{{\bf{w}},b} }&{\frac{{{{\hat \gamma }_i}}}{{{||\bf{w}||}}}}\\ {{\rm{s}}.{\rm{t}}.}&{{y_i}\left( {{\bf{w}} \cdot {x_i} + b} \right) \ge {{\hat \gamma }_i},\quad i = 1,2, \cdots ,n} \end{array}

{% endraw %}

事实上函数间隔 ${\hat \gamma }$ 并不影响最优化问题的解，假设将 $\bf{w}$ 和 $b$ 成倍的改变为 $a\bf{w}，ab$ ，那么函数间隔也会相应变成 $a{\hat \gamma }$ ，因此为简便，我们取 ${\hat \gamma }=1$ ，因此优化函数为最大化 $1/||\bf{w}||$ ，这等价于最小化 $||\bf{w}||$ ，考虑到求导方便，我们最小化 $1/2||\bf{w}||^2$
优化函数最终为：

{% raw %}

\begin{array}{*{20}{l}} {\mathop {\min }\limits_{{\bf{w}},b} }&{\frac{1}{2}||{\bf{w}}|{|^2}}\\ {{\rm{s}}.{\rm{t}}.}&{{y_i}\left( {{\bf{w}} \cdot {{\bf{x}}_i} + b} \right) - 1 \ge 0,\quad i = 1,2, \cdots ,n} \end{array}

{% endraw %}

拉格朗日对偶求极值

写成拉格朗日优化的格式：

{% raw %}

\begin{array}{*{20}{l}} {\mathop {\min }\limits_{{\bf{w}},b} }&{\frac{1}{2}||{\bf{w}}|{|^2}}\\ {{\rm{s}}.{\rm{t}}.}&1-{{y_i}\left( {{\bf{w}} \cdot {{\bf{x}}_i} + b} \right) \le 0,\quad i = 1,2, \cdots ,n} \end{array}

{% endraw %}

拉格朗日方程：

{% raw %}

L({\bf{w}},b,{\bf{\alpha }}) = \frac{1}{2}||{\bf{w}}|{|^2} + \sum\limits_{i = 1}^n {{\alpha _i}(1 - {y_i}\left( {{\bf{w}} \cdot {{\bf{x}}_i} + b} \right)} )

{% endraw %}

原始问题为凸优化问题，我们按照KKT条件求解该问题的对偶问题，即可根据强对偶条件获得原始问题的解
对偶问题为：

{% raw %}

\mathop {max}\limits_{\bf{\alpha }} D({\bf{\alpha }}) = \mathop {max}\limits_{\bf{\alpha }} \mathop {\min }\limits_{{\bf{w}},b} L({\bf{w}},b,{\bf{\alpha }})

{% endraw %}

先求最小化极值问题{% raw %} $\mathop {\min }\limits_{{\bf{w}},b} L({\bf{w}},b,{\bf{\alpha }})$ {% endraw %}：

{% raw %}

\left\{ {\begin{array}{*{20}{c}} {\frac{{\partial {\rm{L}}}}{{\partial {\bf{w}}}} = 0}\\ {\frac{{\partial {\rm{L}}}}{{\partial b}} = 0} \end{array}} \right.

{% endraw %}

解得：

{% raw %}

\left\{ {\begin{array}{*{20}{c}} {{\bf{w}} = \sum\limits_{i = 1}^n {{\alpha _i}{y_i}{{\bf{x}}_i}} }\\ {\sum\limits_{i = 1}^n {{\alpha _i}{y_i} = 0} } \end{array}} \right.

{% endraw %}

带入 $L({\bf{w}},b,{\bf{\alpha }})$ 得：

{% raw %}

\begin{aligned} L(\bf{w}, b, \bf{\alpha}) &=\frac{1}{2}\|\bf{w}\|^{2}+\sum_{i=1}^{n} \alpha_{i}\left[1-y_{i}\left(\bf{w}^{T} x_{i}+b\right)\right] \\ &=\frac{1}{2} \bf{w}^{T} \bf{w}-\bf{w}^{T} \sum_{i=1}^{n} \alpha_{i} y_{i} x_{i}-b \sum_{i=1}^{n} \alpha_{i} y_{i}+\sum_{i=1}^{n} \alpha_{i} \\ &=\frac{1}{2} \bf{w}^{T} \sum_{i=1}^{n} \alpha_{i} y_{i} x_{i}-\bf{w}^{T^{\prime}} \sum_{i=1}^{n} \alpha_{i} x_{i} y_{i}-b * 0+\sum_{i=1}^{n} \alpha_{i} \\ &=\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2}\left(\sum_{i=1}^{n} \alpha_{i} y_{i} x_{i}\right)^{T} \sum_{i=1}^{n} \alpha_{i} y_{i} x_{i} \\ &=\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j} x_{i}^{T} x_{j} \end{aligned}

{% endraw %}

此时我们需要解决的优化问题是：

{% raw %}

\begin{array}{*{20}{c}} {\mathop {\max }\limits_{\bf{\alpha }} \sum\limits_{i = 1}^n {{\alpha _i}} - \frac{1}{2}\sum\limits_{i,j = 1}^n {{\alpha _i}} {\alpha _j}{y_i}{y_j}{\bf{x}}_i^T{{\bf{x}}_j}}\\ {\qquad \begin{array}{*{20}{c}} {{\rm{ s}}{\rm{.t}}{\rm{. }}{\alpha _i} \ge 0,\quad i = 1,2, \ldots ,n}\\ {\sum\limits_{i = 1}^n {{\alpha _i}} {y_i} = 0} \end{array}} \end{array}

{% endraw %}

可以看到通过拉格朗日对偶，我们将原始拉格朗日方程 $k+1+n$ 个未知数、 $n$ 个复杂不等式约束条件的优化问题转换为了 $n$ 个未知数，1个等式约束的问题，当然满足KKT条件是前提
对于这个问题，我们有更高效的优化算法，即序列最小优化（SMO）算法。我们通过这个优化算法能得到 $\bf{α}$ ，再根据 $\bf{α}$ ，我们就可以求解出 $\bf{w}$ 和 $b$ ，进而求得我们最初的目的：找到超平面，即"决策平面"。

SVM 的推导

概述

目标函数

拉格朗日对偶求极值

参考资料