「这是我参与2022首次更文挑战的第8天,活动详情查看:2022首次更文挑战」。
@TOC

前言
Hello!小伙伴!
非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称:海轰
标签:程序猿|C++选手|学生
简介:因C语言结识编程,随后转入计算机专业,有幸拿过一些国奖、省奖...已保研。目前正在学习C++/Linux/Python
学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语!
机器学习小白阶段
文章仅作为自己的学习笔记 用于知识体系建立以及复习
知其然 知其所以然!
往期文章
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(1):集合与映射
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(2):线性空间定义及其性质
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(3):线性空间的基与坐标
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(4):基变换与坐标变换
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(5):线性子空间
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(6):子空间的交与和
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(7):欧氏空间
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(8):标准正交基与Gram-Schmidt过程
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(9):正交补与投影定理
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(10):线性变换定义
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(11):线性变换的矩阵表示
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(12):相似形理论
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(13):Hamliton-Cayley定理、最小多项式
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(14):向量范数及其性质
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(15):矩阵的范数
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(16):向量和矩阵的极限
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(17):函数矩阵的微分和积分
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(18):方阵的幂级数
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(19):不定积分(补充知识)
5.4 方阵函数
5.4.1 方阵函数f(A)定义
最简单的方阵函数是矩阵多项式
B=f(A)=a0E+a1A+...+anAn
其中A∈Cn×n,ai∈C
简单理解:以前知识中函数形式为:f(x)=a0+a1x+...+anxn
在这里,变量x变为了矩阵A
得到:f(A)=a0E+a1A+...+anAn
5.4.2 用方阵A的若当形计算方阵函数f(A)
定理5.4.1
若方阵X∈Cn×n的幂级数∑k=0∞akXk收敛,并记
f(X)=∑k=0∞akXk
则当
X=diag(X1,X2,...,Xt)
有
f(X)=f(diag(X1,X2,...,Xt))=diag(f(X1),f(X2),...,f(Xt))
diag:对角矩阵
这个定理的大概意思是说:若X可以变换为对角阵时,f(X)可以等效为diag(f(X1),f(X2),...,f(Xt))
定理5.4.2
任给收敛半径为R的复变幂级数
f(z)=∑k=0∞akzk
及一个n阶Jordan块
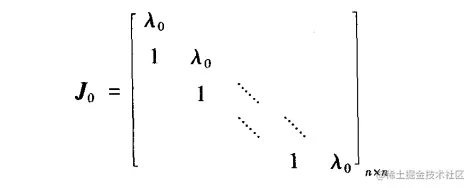 则当∣λ0∣<R时,级数
则当∣λ0∣<R时,级数
∑k=0∞akJ0k
绝对收敛,且
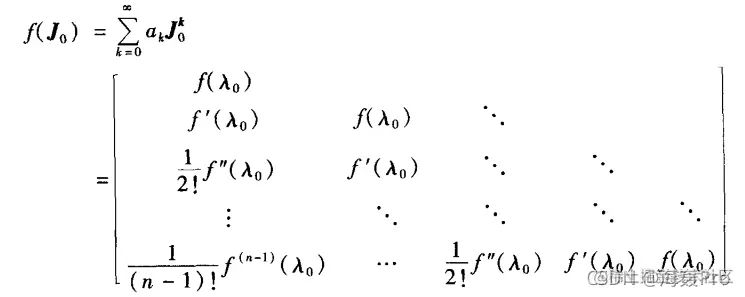
这个定理的大概意思是说:
若X不可以变换为对角阵,但可以变换为若当矩阵时
f(X)可以等效为上图矩阵
利用A的标准形状计算方阵函数f(A)
当A与对角形相似时,即存在可逆矩阵P,使
A=P[diag(λ1,λ2,...,λn)]P−1
则对于复变幂级数
f(z)=∑k=0∞akzk∣z∣<R
当ρ(A)<R时,矩阵幂级数
f(A)=∑k=0∞akAk
收敛,且
f(A)=f(P[diag(λ1,λ2,...,λn)]P−1)=P[diag(f(λ1),f(λ2),...,f(λn))]P−1
例:设A=[001−2],求eA,sin(A),cos(A)

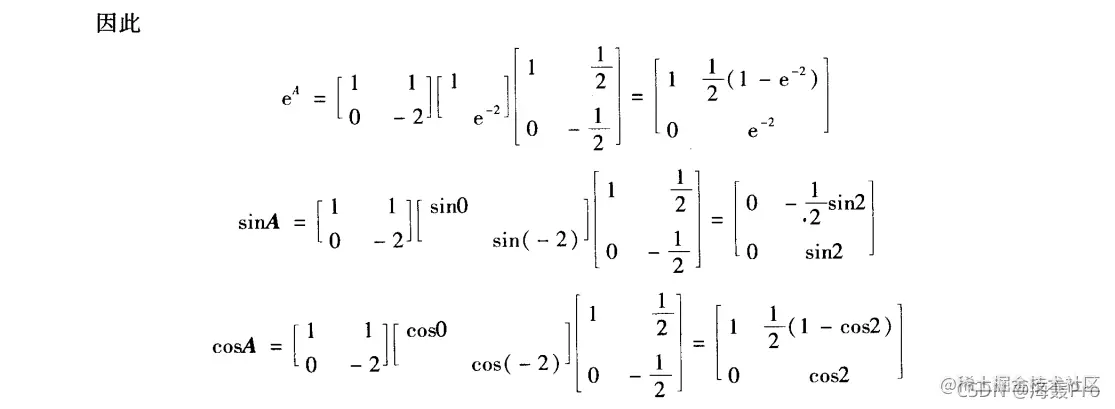
一般遇到的方阵函数往往不是常数矩阵A的函数
而是变量t的函数矩阵At的函数
即尚须计算方阵函数eAt,sin(At),cos(At),计算方法同上面一样,即
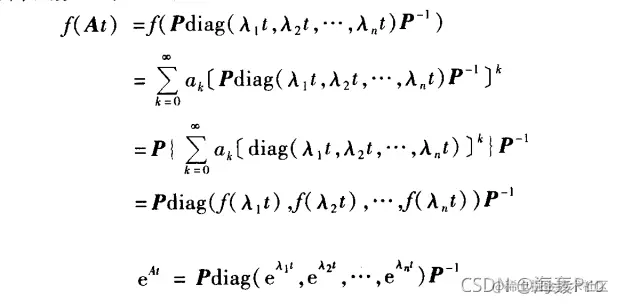
当A不与对角形矩阵相似时,即存在可逆矩阵P,使得

例:设A=⎣⎡002103010⎦⎤,求eA
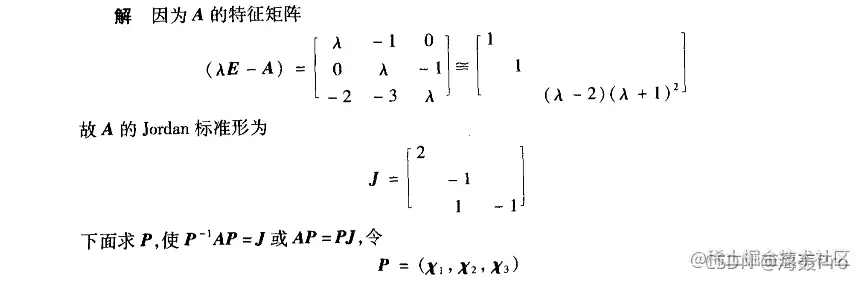
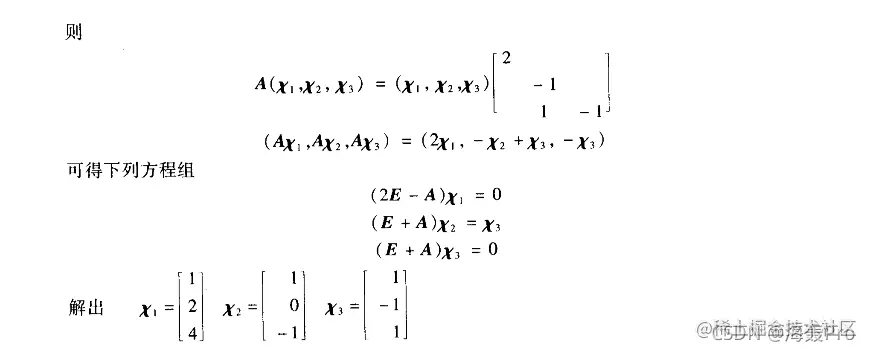
 若是求eAt,则为
若是求eAt,则为
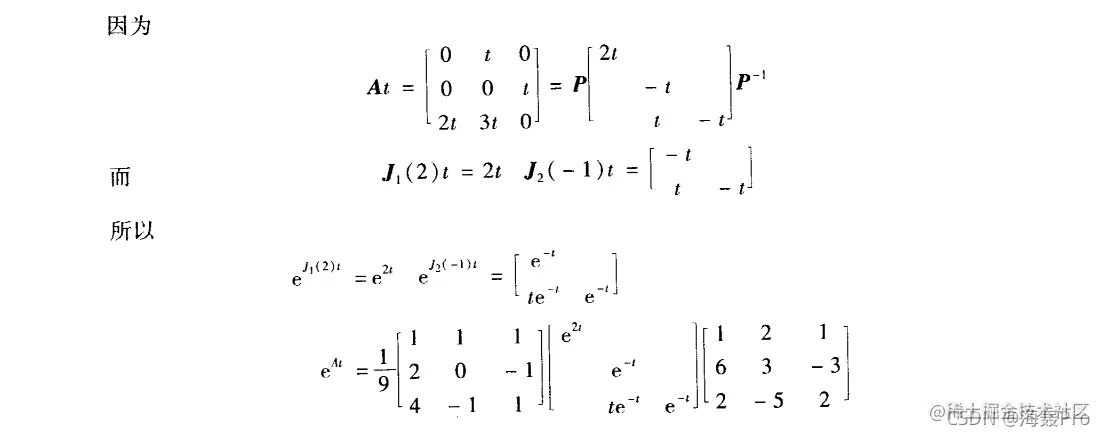
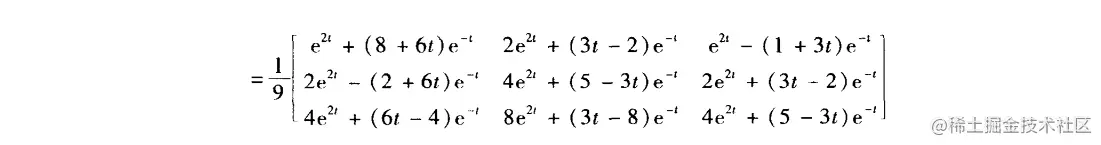
5.4.3 用f(z)在A上的谱值方法计算方阵函数f(A)
设h(λ)是有限次多项式,m(λ)是方阵A的最小多项式(令deg[m(λ)]=t),用m(λ)去除h(λ),其商为g(λ),余式为r(λ),便有
h(λ)=m(λ)g(λ)+r(λ)
有deg[r(λ)]≤t−1,或r(λ)=0
deg[m(λ)]:多项式m(λ)的最高次数
比如m(λ)=4λ2+λ+3
则deg[m(λ)]=2
由m(A)=0,有
h(A)=m(A)g(A)+r(A)
说明方阵A的一个任意多项式h(A)总可以表示为A的次数不超过t−1的多项式r(A)
t是A的最小多项式m(λ)的次数
也就是说,方阵A的任何有限次多项式h(A)都可以被E,A,...,At−1线性表示,且E,A,...,At−1是线性无关的
r(A)是唯一的
因为方阵函数f(A)=∑k=0∞akAk的幂级数表达式收敛,而Ak(k≥t)又可以表示为A的次数不超过t−1的多项式
则可以把f(A)表示为次数不超过t−1的方阵多项式T(A)
因为任意一个Ak都可以表示为一个次数不超过t−1的多项式
所以A1+A2+...+Ak结果一定也是次数不超过t−1的多项式
定义5.9
设n阶方阵A的最小多项式为
m(λ)=(λ−λ1)t1(λ−λ2)t2....(λ−λs)ts
其中λ1,λ2,...,λs是A的互不相同的特征根
如果复函数f(z)及其各阶导数f(l)(z)在z=λi(i=1,2,...,s)处的导数值,即
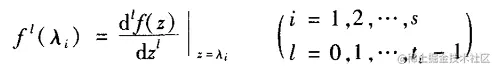 均为有限值,便称函数f(z)在方阵A的谱上给定,并称这些值为f(z)在A上的谱值
均为有限值,便称函数f(z)在方阵A的谱上给定,并称这些值为f(z)在A上的谱值
定理5.4.3
设A∈Cn×n的最小多项式为
m(λ)=(λ−λ1)t1(λ−λ2)t2....(λ−λs)ts
其中t1+t2+...+ts=t,λi=λj(i=j,i,j=1,2,...,s)
其实这里的t就是deg[m(λ)]
而方阵函数f(A)是收敛的方阵幂级数∑k=0∞akAk的和函数,级
f(A)=∑k=0∞akAk
设
T(λ)=b0+b1λ+...+bt−1λt−1
使得
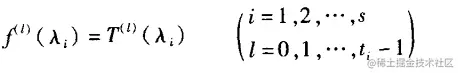
则有
T(A)=f(A)=∑k=0∞akAk
例:设A=[001−2],计算eAz

例:设A=[54−4−3],计算A100

结语
说明:
- 参考于 课本《矩阵理论》
- 配合书中概念讲解 结合了自己的一些理解及思考
文章仅作为学习笔记,记录从0到1的一个过程
希望对您有一点点帮助,如有错误欢迎小伙伴指正

则当时,级数
若是求,则为
均为有限值,便称函数在方阵的谱上给定,并称这些值为在上的谱值