Floyd核心

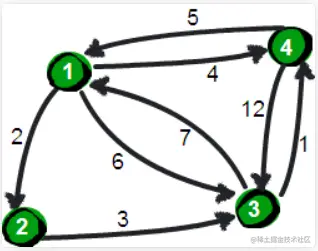
• 假如现在只允许经过1号顶点，求任意两点之间的最短路程，应该如何求呢？只需判断e[i][1]+e[1][j]是否比e[i][j]要小即可。e[i][j]表示的是从i号顶点到j号顶点之间的路程。e[i][1]+e[1][j]表示的是从i号顶点先到1号顶点，再从1号顶点到j号顶点的路程之和。其中i是1-n循环，j也是1-n循环，代码实现如下。

for (i = 1; i <= n; i++)
 {
     for (j = 1; j <= n; j++)
     {
        if (e[i][j] > e[i][1] + e[1][j])
             e[i][j] = e[i][1] + e[1][j];
    }
 }

• 接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短路程。如何做呢？我们需要在只允许经过1号顶点时任意两点的最短路程的结果下，再判断如果经过2号顶点是否可以使得i号顶点到j号顶点之间的路程变得更短。即判断e[i][2]+e[2][j]是否比e[i][j]要小，代码实现为如下。

1 //经过1号顶点
2 for(i=1;i<=n;i++)  
3 for(j=1;j<=n;j++)  
4 if (e[i][j] > e[i][1]+e[1][j])  e[i][j]=e[i][1]+e[1][j];  
5 //经过2号顶点
6 for(i=1;i<=n;i++)  
7 for(j=1;j<=n;j++)  
8 if (e[i][j] > e[i][2]+e[2][j])  e[i][j]=e[i][2]+e[2][j]; 

• 现在规律其实已经很明显，若允许经过n号顶点的情况下的任意两点之间的最短路程，其实只需要在最外一层再包一层循环即可

for(k=1;k<=n;k++)  
     for(i=1;i<=n;i++)  
     for(j=1;j<=n;j++)  
     if(e[i][j]>e[i][k]+e[k][j])  
                      e[i][j]=e[i][k]+e[k][j];  

399. 除法求值

class Solution {
    public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
        int nvars=0;
        Map<String,Integer> hashMap=new HashMap<>();
        int equationsLen=equations.size();
        for(int i=0;i<equationsLen;i++){
            if(!hashMap.containsKey(equations.get(i).get(0)))
                hashMap.put(equations.get(i).get(0),nvars++);
            if(!hashMap.containsKey(equations.get(i).get(1)))
                hashMap.put(equations.get(i).get(1),nvars++);
        }
        double[][] graph=new double[nvars][nvars];
        //初始化图数组
        for(int i=0;i<nvars;i++){
            Arrays.fill(graph[i],-1.0);
        }
        for(int i=0;i<equationsLen;i++){
            int va=hashMap.get(equations.get(i).get(0)),vb=hashMap.get(equations.get(i).get(1));
            graph[va][vb]=values[i];
            graph[vb][va]=1/values[i];
        }
        //Floyd核心
        for(int k=0;k<nvars;k++){
            for(int i=0;i<nvars;i++){
                for(int j=0;j<nvars;j++){
                    if(graph[i][k]>0&&graph[k][j]>0)
                        graph[i][j]=graph[i][k]*graph[k][j];
                }
            }
        }
        int queriesLen=queries.size();
        double[] ans=new double[queriesLen];
        for(int i=0;i<queriesLen;i++){
            if(hashMap.containsKey(queries.get(i).get(0))&&hashMap.containsKey(queries.get(i).get(1))){
                int va=hashMap.get(queries.get(i).get(0)),vb=hashMap.get(queries.get(i).get(1));
                ans[i]=graph[va][vb];
            }else
                ans[i]=-1.0;            
        }
        return ans;
    }
}