拉格朗日乘数法

已注销
1,459 阅读5分钟

「这是我参与2022首次更文挑战的第5天，活动详情查看：2022首次更文挑战」。

在数学最优问题中，拉格朗日乘数法（以数学家约瑟夫·路易斯·拉格朗日命名）是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束。本文介绍拉格朗日乘数法（Lagrange multiplier）。

概述

  • 我们擅长解决的是无约束极值求解问题，这类问题仅需对所有变量求偏导，使得所有偏导数为0，即可找到所有极值点和鞍点。我们解决带约束条件的问题时便会尝试将其转化为无约束优化问题

  • 事实上如果我们可以通过g得到某个变量的表示，例如x1=h(x2,...,xn)x_1 = h(x_2, ..., x_n)，将该式带入yy即可抓换为无约束优化（初高中就是这么做的，所谓消元法是也），但有的时候我们无法得到这样的表示，便需要借助拉格朗日乘数法来避免消元法的困境。

作为一种优化算法，拉格朗日乘数法主要用于解决约束优化问题，它的基本思想就是通过引入拉格朗日乘子来将含有nn个变量和k个k个约束条件的约束优化问题转化为含有（n+k）（n+k）个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。

思想

  • 考虑二元函数f(x,y)f(x,y)，在约束g(x,y)=cg(x,y)=c下的极值
  • 首先我们可以绘制出f(x,y)f(x,y)的一层层等高线，当等高线与g(x,y)=cg(x,y)=c相切时即可能是该问题的极值点

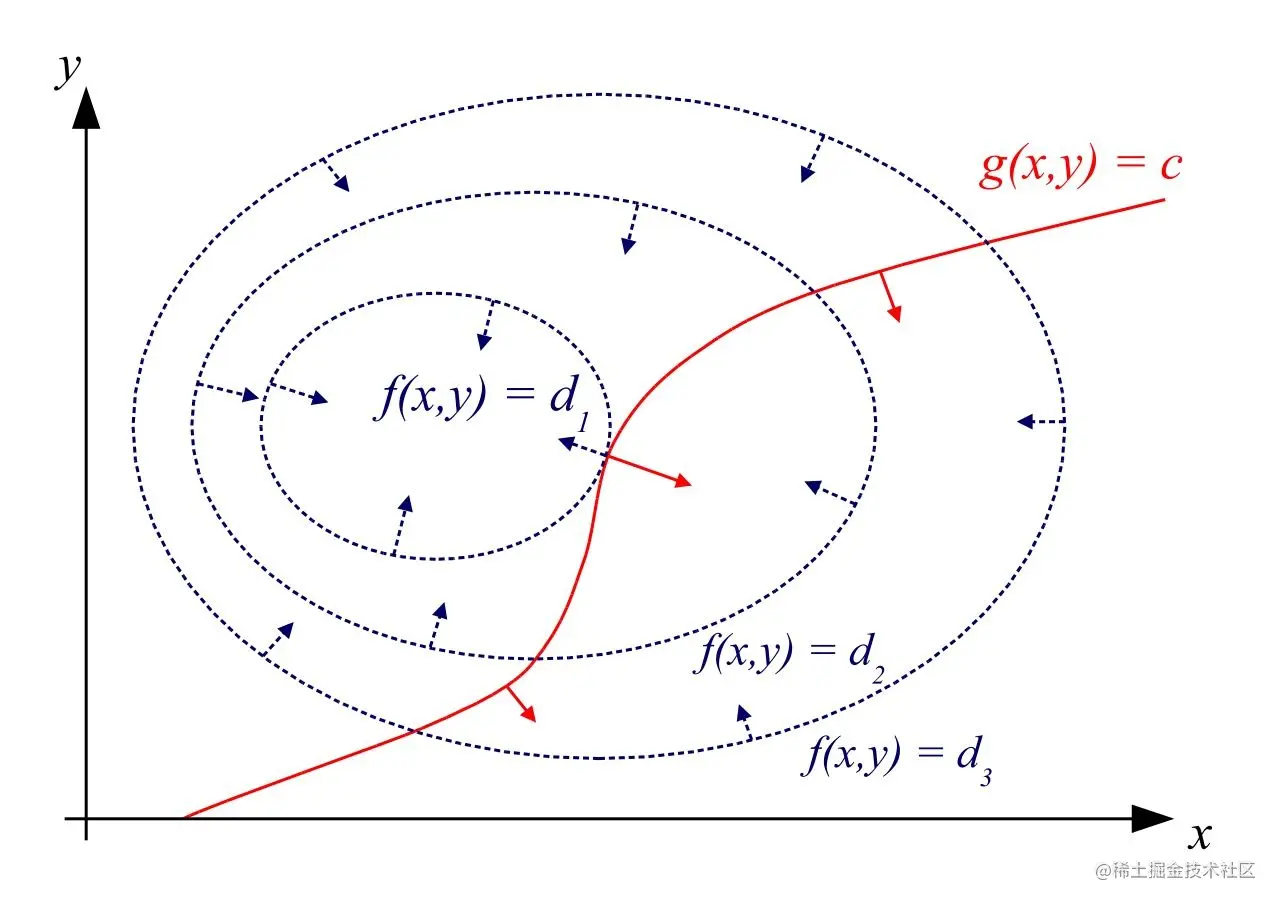
拉格朗日乘数法示意图（转自知乎）

拉格朗日乘数法

单个等式约束

考虑nn元函数y=f(x1,x2,...,xn)y=f(x_1, x_2,...,x_n)，在等式约束g(x1,x2,...,xn)=0g(x_1, x_2,...,x_n)=0 下的极值点求解问题

  • 在极值点，必有yy和gg法向量平行
  • yy的法向量为：

{% raw%}

[∂y∂x1,∂y∂x2,...,∂y∂xn][\frac{{\partial y}}{{\partial {x_1}}},\frac{{\partial y}}{{\partial {x_2}}},...,\frac{{\partial y}}{{\partial {x_n}}}]

{% endraw%}

  • gg的法向量为：

{% raw%}

[∂g∂x1,∂g∂x2,...,∂g∂xn][\frac{{\partial g}}{{\partial {x_1}}},\frac{{\partial g}}{{\partial {x_2}}},...,\frac{{\partial g}}{{\partial {x_n}}}]

{% endraw%}

  • 二者平行，则存在常数λ\lambda使得：

{% raw%}

[∂y∂x1,∂y∂x2,...,∂y∂xn]+λ[∂g∂x1,∂g∂x2,...,∂g∂xn]=0[\frac{{\partial y}}{{\partial {x_1}}},\frac{{\partial y}}{{\partial {x_2}}},...,\frac{{\partial y}}{{\partial {x_n}}}] + \lambda [\frac{{\partial g}}{{\partial {x_1}}},\frac{{\partial g}}{{\partial {x_2}}},...,\frac{{\partial g}}{{\partial {x_n}}}] = 0

{% endraw%}

  • 即：

{% raw%}

∂y∂xi+λ∂g∂xi=0,1≤i≤n\frac{{\partial y}}{{\partial {x_i}}} + \lambda \frac{{\partial g}}{{\partial {x_i}}} = 0,1 \le i \le n

{% endraw%}

  • 这样我们就得到了nn个等式方程，再加上g(x1,x2,...,xn)=0g(x_1, x_2,...,x_n)=0一起构成n+1n+1个方程的方程组，未知数为[x1,x2,...,xn,λ][x_1,x_2,...,x_n,\lambda]共n+1n+1个，方程组的解即为所有极值点和鞍点的集合，每组解中的λ\lambda即为两个平行法向量的倍数，该值在等式约束轨迹穿过yy的极值点时为0。

多个等式约束

原理与单个等式约束情况类似

考虑nn元函数y=f(x1,x2,...,xn)y=f(x_1, x_2,...,x_n)，在mm个等式约束(gi(x1,x2,...,xn)=0,1≤i≤mg_i(x_1, x_2,...,x_n)=0, 1 \le i \le m) 下的极值点求解问题

  • nn维空间由mm个条件约束，会确定一个n−mn-m维的曲面，我们讨论yy在这个曲面上的极值问题
  • 这个曲面由mm个n−1n-1维曲面交织而成，存在mm个法向量，这mm个法向量构成了n−mn-m维曲面的法空间
  • 在问题的极值点，yy的法向量必然落在n−mn-m维曲面的法空间之内，也就是说yy的法向量可以由n−mn-m维曲面的mm个法向量的线性组合表示：

{% raw%}

[∂y∂x1,∂y∂x2,...,∂y∂xn]+∑i=1mλi[∂gi∂x1,∂gi∂x2,...,∂gi∂xn]=0[\frac{{\partial y}}{{\partial {x_1}}},\frac{{\partial y}}{{\partial {x_2}}},...,\frac{{\partial y}}{{\partial {x_n}}}] + \sum\limits_{i = 1}^m {{\lambda _i}[\frac{{\partial {g_i}}}{{\partial {x_1}}},\frac{{\partial {g_i}}}{{\partial {x_2}}},...,\frac{{\partial {g_i}}}{{\partial {x_n}}}]} = 0

{% endraw%}

  • 即：

{% raw%}

∂y∂xj+∑i=1mλi∂gi∂xj=0,1≤j≤n\frac{{\partial y}}{{\partial {x_j}}} + \sum\limits_{i = 1}^m {{\lambda _i}\frac{{\partial {g_i}}}{{\partial {x_j}}}} = 0,1 \le j \le n

{% endraw%}

  • 此时我们得到了nn个等式方程，再加上mm个等式约束(gi(x1,x2,...,xn)=0,1≤i≤mg_i(x_1, x_2,...,x_n)=0, 1 \le i \le m) 一起构成n+mn+m个方程的方程组，未知数为[x1,x2,...,xn,λ1,λ2,...,λm][x_1,x_2,...,x_n,\lambda_1,\lambda_2,...,\lambda_m]共n+mn+m个，方程组的解即为所有极值点和鞍点的集合，每组解中的λi\lambda_i的值即为yy的法向量在n−mn-m维曲面的法空间中的线性组合系数。

单个不等式约束

不等式约束其实是等式约束的扩展，等式约束表示一组确定的等高线（面），不等式约束则表示等高线（面）的某一边区域

考虑nn元函数y=f(x1,x2,...,xn)y=f(x_1, x_2,...,x_n)，在不等式约束g(x1,x2,...,xn)≤0g(x_1, x_2,...,x_n) \le 0 下的极值点求解问题

  • 若该问题有解，那么有两种情况
  1. 解在 g(x1,x2,...,xn)=0g(x_1, x_2,...,x_n) = 0 曲面上
  2. 解在g(x1,x2,...,xn)<0g(x_1, x_2,...,x_n) < 0 范围内
  • 当解在 g(x1,x2,...,xn)=0g(x_1, x_2,...,x_n) = 0 曲面上时，说明该不等式对yy取最小值的区域进行了限制，最终解落在了yy和约束相切的位置，那么此时二者的法向量方向必然相反（否则yy会在g(x1,x2,...,xn)<0g(x_1, x_2,...,x_n) < 0 范围内找到更小的值），按照等式情况构建方程：

{% raw%}

∂y∂xi+λ∂g∂xi=0,1≤i≤n\frac{{\partial y}}{{\partial {x_i}}} + \lambda \frac{{\partial g}}{{\partial {x_i}}} = 0,1 \le i \le n

{% endraw%}

  • 便有结论：λ≥0\lambda \ge 0

  • 当解在g(x1,x2,...,xn)<0g(x_1, x_2,...,x_n) < 0 范围内时，事实上这个不等式没有对yy的求解起到约束作用，此时相当于λ=0\lambda = 0

  • 而且两种情况下分别有 g(x1,x2,...,xn)=0g(x_1, x_2,...,x_n) = 0和λ=0\lambda = 0，也就是二者必有一方为0

  • 因此对于单个不等式约束的拉格朗日乘数法，仅需增加限制条件： λ≥0\lambda \ge 0和λg(x1,x2,...,xn)=0\lambda g(x_1, x_2,...,x_n) = 0

多个不等式约束

考虑nn元函数y=f(x1,x2,...,xn)y=f(x_1, x_2,...,x_n)，在mm个不等式约束(gi(x1,x2,...,xn)≤0,1≤i≤mg_i(x_1, x_2,...,x_n)\le0, 1 \le i \le m) 下的极值点求解问题

  • 本质上与单个不等式约束相同，只是数量变多了
  • 此情况下需要在等式拉格朗日乘数法基础上增加条件：

{% raw%}

λi≥0,1≤i≤mλigi=0,1≤i≤m\begin{aligned} \lambda_i &\ge 0,1 \le i \le m\\ \lambda_ig_i &= 0,1 \le i \le m \end{aligned}

{% endraw%}

算法描述

  • 基于上述原理，提出了拉格朗日乘数法：

  1. 考虑nn元函数y=f(x1,x2,...,xn)y=f(x_1, x_2,...,x_n)，在m1m_1个等式约束(gi(x1,x2,...,xn)=0,1≤i≤m1g_i(x_1, x_2,...,x_n)=0, 1 \le i \le m_1) 、m2m_2个不等式约束(hj(x1,x2,...,xn)≤0,1≤j≤m2h_j(x_1, x_2,...,x_n)\le0, 1 \le j \le m_2) 下的极值点求解问题

  2. 加入常数λ,μ\lambda,\mu构造方程：

{% raw%}

z=f(x1,x2,...,xn)+∑i=1m1λigi(x1,x2,...,xn)+∑j=1m2μjhj(x1,x2,...,xn)z = f({x_1},{x_2},...,{x_n}) + \sum\limits_{i = 1}^{{m_1}} {{\lambda _i}{g_i}({x_1},{x_2},...,{x_n})} + \sum\limits_{j = 1}^{{m_2}} {{\mu _j}{h_j}({x_1},{x_2},...,{x_n})}

{% endraw%}

  1. 对所有变量求偏导，并令导数为0：

{% raw%}

∂z∂xi=0∂y∂xk+∑i=1m1λi∂g∂xk+∑j=1m1μj∂h∂xk=0\begin{aligned} \frac{{\partial z}}{{\partial {x_i}}} &= 0\\ \frac{{\partial y}}{{\partial {x_k}}} + \sum\limits_{i = 1}^{{m_1}} {{\lambda _i}\frac{{\partial g}}{{\partial {x_k}}}} + \sum\limits_{j = 1}^{{m_1}} {{\mu _j}\frac{{\partial h}}{{\partial {x_k}}}} {\rm{ }} &= 0 \end{aligned}

{% endraw%}

其中：1≤k≤n1 \le k \le n

  1. 将上述nn个方程与m1m_1个等式约束方程gi(x1,x2,...,xn)=0,1≤i≤m1g_i(x_1, x_2,...,x_n)=0, 1 \le i \le m_1 联立
  2. 将上述n+m1n+m_1个方程与μjhj=0,1≤j≤m2\mu_j h_j=0, 1 \le j \le m_2联立，得到n+m1+m2n+m_1+m_2个方程
  3. 加上限制条件μj≥0\mu_j \ge 0，h_j \le 0$$, 1 \le j \le m_2
  4. 在限制条件下解n+m1+m2n+m_1+m_2元方程即可得到极值点与鞍点集合
  5. 从所有解中筛选出极值点

KKT条件

  • 上述n+m1+m2n+m_1+m_2元方程与限制条件即为KKT条件
  • KKT条件是拉格朗日函数取极值时的必要条件

{% raw %}

{∇f+∑im1λi∇gi+∑jm2μj∇hj=0gi=0,hj≤0,μj≥0,μjhj=0\left\{\begin{array}{l} \nabla f+\sum_{i}^{m_1} \lambda_{i} \nabla g_{i}+\sum_{j}^{m_2} \mu_{j} \nabla h_{j}=0 \\ g_{i}=0, \\ h_{j} \leq 0, \\ \mu_{j} \geq 0, \\ \mu_{j} h_{j}=0\\ \end{array}\right.

{% endraw %}

其中 i∈{1,2,⋯ ,m1}i \in \{ 1,2, \cdots, m_1\} ，j∈{1,2,⋯ ,m2}j \in \{ 1,2, \cdots, m_2\}

  • 总结一下所有条件的含义：
内容含义
{% raw%}∇f+∑im1λi∇gi+∑jm2μj∇hj=0\nabla f+\sum_{i}^{m_1} \lambda_{i} \nabla g_{i}+\sum_{j}^{m_2} \mu_{j} \nabla h_{j}=0{% endraw%}求解极值需要在各个自变量方向上导数为0
gi=0g_{i}=0等式约束
hj≤0h_{j} \le 0不等式约束
μj≥0\mu_{j} \geq 0不等式约束时的两种情况：
1. 不等式约束无效(μj=0\mu_{j} = 0)
2. 不等式分界面法向量与原函数法向量方向相反(μj>0\mu_{j} > 0)
μjhj=0\mu_{j} h_{j}=0不等式约束时的两种情况：
1. 不等式约束无效，极值点在hj<0h_{j} < 0范围内 (μj=0\mu_{j} = 0)
2. 不等式约束有效，极值点在hj=0h_{j} = 0曲面上(hj=0h_{j} = 0)

参考资料

avatar
文章
阅读
粉丝