交叉熵（the cross-entropy）代价函数的详细介绍及推导过程

用户353802075153
182 阅读6分钟

为什么要引入交叉熵代价函数

首先我们先来看一个小例子，它的功能是将输入的数字进行取反然后输出，例如输入1需要输出0，在设置ww和bb的初始值时，我们设置了两种不同的取值，在第一个模型中，我们取的参数值为w=0.6,b=0.9w=0.6,b=0.9，在第二个模型中，我们取的参数值为w=2,b=2w=2,b=2，其具体的训练过程可以参照这里的前两个动画，可以看到对于第二个模型，开始个结束的时候学习速度均很慢，如下图，这种行为看起来和人类学习的行为差异很大，我们通常是在犯错误比较明显的时候学习速度最快。但是在上例的两个动画中我们看到的却与我们的常理不太相符。

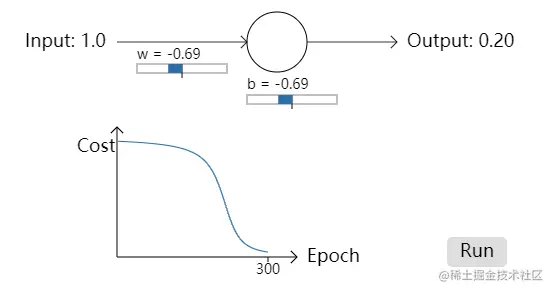
image-20220114012252730

为了理解这个问题，我们需要清楚其学习的速率到底是怎么来的，我们已经知道，神经元是通过改变权重和偏置，并以代价函数的偏导数∂C∂w\frac {\partial C} {\partial w}和∂C∂b\frac{\partial C}{\partial b}来决定学习的速度，所以，在说到”学习速度“较慢的时候，实际上就是说这两个的偏导数很小。

C=(y−a)22(1)C=\frac {(y-a)^2}{2} \tag1

我们首先先求得这两个偏导数：

对于上面动画中的功能，是一个简单的将输入的数字取反的函数，因此我们假设输入输出为x=1,y=0x=1,y=0，代入后可以得到下面式子的最后一项

∂C∂w=(a−y)σ′(z)x=aσ′(z)(2)\frac {\partial C} {\partial w}=(a-y)\sigma '(z)x=a\sigma'(z) \tag2
∂C∂b=(a−y)σ′(z)=aσ′(z)(3)\frac{\partial C}{\partial b}=(a-y)\sigma '(z)=a\sigma'(z) \tag3

σ′(z)=σ(z)(1−σ(z))(4)\sigma'(z)=\sigma(z)(1-\sigma(z)) \tag4

对于式4可以自己推导算一下

为了理解表达式的具体行为，我们可以具体的看一下σ′\sigma '这一项，首先先回想一下σ\sigma函数的图像：

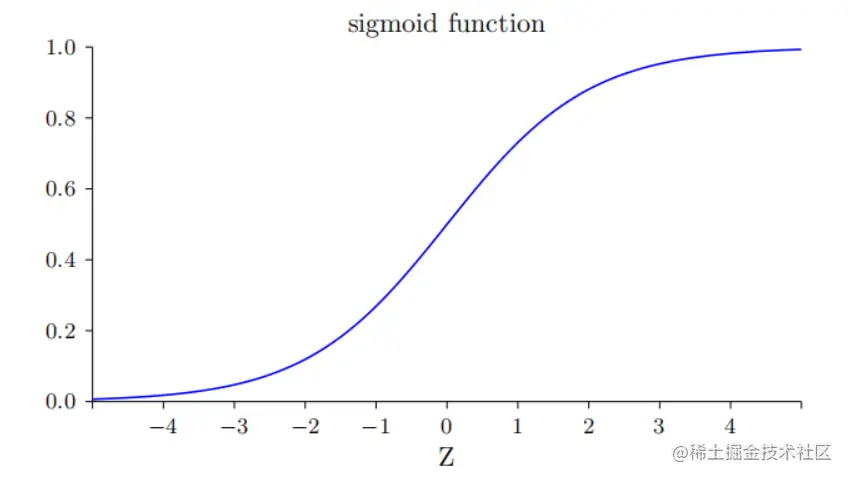
image-20220113190102657

我们可以看到，当神经元的输出接近1的时候，曲线会变得相当平，所以σ′(z)\sigma'(z)就很小，因此在开始的时候两个偏导数都很小，学习速率自然也就很慢了，所以提出交叉熵就是为了解决这种明明离正确结果很远但是速率缺很慢的情况，也就是为了消除σ′\sigma'对于我们训练速度的影响。

在第一个模型中，取得初始参数值为w=0.6,b=0.9w=0.6,b=0.9，则

z=wx+b=1.5σ(z)=11+e−z=11+e−1.5=0.81σ′(z)=0.81×(1−0.81)=0.1539z=wx+b=1.5\\ \sigma(z)=\frac 1 {1+e^{-z}}=\frac 1 {1+e^{-1.5}}=0.81\\ \sigma'(z)=0.81 \times(1-0.81)=0.1539

在第二个模型中，取得初始参数值为w=2.0,b=2.0w=2.0,b=2.0，则

z=wx+b=4σ(z)=11+e−z=11+e−4=0.98σ′(z)=0.98×(1−0.980.0196)=0.1539z=wx+b=4\\ \sigma(z)=\frac 1 {1+e^{-z}}=\frac 1 {1+e^{-4}}=0.98\\ \sigma'(z)=0.98 \times(1-0.980.0196)=0.1539

可以看到在第二个模型中，其初始的σ′\sigma' 比第一个中的初始的σ′\sigma' 小的多，因此其速率自然慢很多

交叉熵代价函数长什么样

对于交叉熵代价函数我们如下定义：

C=−1n∑x[yln⁡a+(1−y)ln⁡(1−a)](5)C=-\frac 1 n \sum_x [y\ln a + (1-y) \ln (1-a)] \tag5

其中n是训练数据的总数，求和是在所有的训练输入x上进行的，y是对应的目标输出。

但是我们很难直接看出来他是怎样解决学习缓慢的问题的。实际上，将这个定义看做是一个有效的代价函数也是很不明显的。我们首先来看看一下是如何将其解释为一个代价函数的。

将交叉熵解释称为代价函数有两点原因：

第一：它是非负的，C>0。这一点可以从式(5)的表达式中看出来，函数的预期输出是[0,1][0,1]，这就保证了ln⁡a\ln a 和ln⁡(1−a)\ln (1-a)都是负的，同时，由于最开始有一个符号，则可以保证C的取值永远都是大于0的。

第二：对于所有的训练输入x，如果神经元实际的输出接近目标值，那么交叉熵将接近0。假设在这个例子中，当y=0y=0且a≈0a\approx 0时，第一项yln⁡ay\ln a的值为0，第二项(1−y)ln⁡(1−a)≈0(1-y)\ln (1-a)\approx 0，则可以计算得到C≈0C\approx 0。反之，y=1y=1且a≈1a\approx 1时，C的取值也趋近于0。

综上所述，交叉熵是非负的，并且在神经元的输出与正确结果接近的时候代价函数的值趋近于0，这些就是一个好的代价函数所需要具备的特性。

接下来说一下为什么使用交叉熵代价函数可以避免学习速度下降的问题：

在谈论到学习速度的问题的时候，无论是什么代价函数，我们第一个想到的都应该是两个偏导数的值∂C∂w\frac{\partial C}{\partial w}和∂C∂b\frac{\partial C}{\partial b}，这里我们先讨论前者。

∂C∂wj=−1n∑x(yσ(z)−(1−y)1−σ(z))∂σ∂wj=−1n∑x(yσ(z)−(1−y)1−σ(z))σ′(z)xj=−1n∑xσ′(z)xjσ(z)(1−σ(z))(σ(z)−y)(6)\begin{aligned} \frac{\partial C}{\partial w_j}&=-\frac 1 n \sum_x (\frac y {\sigma (z)}-\frac{(1-y)}{1-\sigma(z)})\frac{\partial \sigma}{\partial w_j}\\ &=-\frac 1 n \sum_x (\frac y {\sigma (z)}-\frac{(1-y)}{1-\sigma(z)})\sigma'(z)x_j\\ &=-\frac 1 n \sum_x \frac{\sigma'(z)x_j}{\sigma(z)(1-\sigma(z))}(\sigma(z)-y) \end{aligned} \tag6

而由式（4）我们可以将式（6）进一步化简称为下面的形式：

利用式子σ′(z)=σ(z)(1−σ(z))\sigma'(z)=\sigma(z)(1-\sigma(z))将分式分子分母化简约分掉

∂C∂wj=−1n∑xxj(σ(z)−y)(7)\frac{\partial C}{\partial w_j}=-\frac 1 n \sum_x x_j(\sigma(z)-y) \tag7

这个式子是一个非常优美的式子，它告诉我们学习的速度受到 σ(z)−y\sigma(z)-y ，也就是输出的误差的控制。这就意味着如果有更大的误差，这我们的模型会有更快的学习速度，这正是我们需要的结果。

特别地，这个式子还避免了像在二次代价函数中类似方程中σ′(z)\sigma '(z)导致的学习缓慢，见方程（2）和方程（3）。这是因为当我们使用交叉熵的时候，σ′(z)\sigma'(z)被约掉了，所以我们不需要关心它是不是变得很小，这就是交叉熵带来的特殊效果。实际上，这也不是非常奇迹的事情，我们可以在后面看到，交叉熵其实只是满足这种特性的一种选择罢了。

根据类似的方法，我们可以计算出关于偏置的偏导数如下，各位可以自己动手算一下：

其实与关于权重的偏导数一样，只不过是在求σ′(z)\sigma'(z)时，z对于w和b的偏导数不一致，根据式子z=wxj+bz=wx_j+b

∂z∂w=xj∂z∂b=1\begin{aligned} &\frac{ \partial z}{\partial w}=x_j\\ &\frac{\partial z}{\partial b}=1 \end{aligned}

可以看出来二者仅相差了xjx_j这一项

∂C∂wj=−1n∑x(σ(z)−y)(8)\frac{\partial C}{\partial w_j}=-\frac 1 n \sum_x (\sigma(z)-y) \tag8

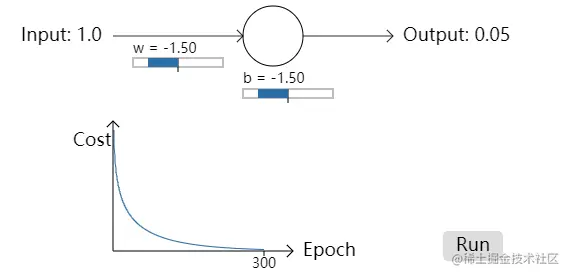
如果使用交叉熵代价函数再去处理开始时提到的取反的问题，我们可以得到非常不一样的代价函数走向，具体可以参考这里的两个动画

对于w=2.0和b=2.0w=2.0和b=2.0的初始条件下，可以看到其在刚开始的下降速度也是非常快的，与使用平方代价函数完全不同，这就是交叉熵代价函数的优势。

image-20220114012102622

补充：交叉熵是怎么推导出来的

首先我们在开头就已经提到了，提出交叉熵就是为了解决这种明明离正确结果很远但是速率缺很慢的情况，也就是为了消除σ′\sigma'对于我们训练速度的影响。因此，很自然的，我们就会想到提出一个对于权重和偏置的偏导数中不包含σ′(z)\sigma '(z)的代价函数。

所以，这个时候对于一个训练样本xx，其代价C=CxC=C_x满足：

其中，a=σ(z),z=w⋅x+ba=\sigma (z),z=w\cdot x+b

∂C∂wj=xj(a−y)∂C∂b=(a−y)(9)\begin{aligned} \frac {\partial C}{\partial w_j}&=x_j(a-y)\\ \frac {\partial C}{\partial b}&=(a-y) \end{aligned} \tag9

如果我们选择的代价函数满⾜这些条件，那么它们就能以简单的⽅式呈现这样的特性：初始误差越⼤，神经元学习得越快。

我们也可以很简单的从数学推导中求出交叉熵的形式：

首先，根据求导的链式法则有：

∂C∂b=∂C∂aσ′(z)(10)\frac {\partial C}{\partial b}=\frac {\partial C}{\partial a}\sigma'(z) \tag{10}

根据式(4)，我们可以得知：σ′(z)=σ(z)(1−σ(z))=a(1−a)\sigma'(z)=\sigma(z)(1-\sigma(z))=a(1-a)，则式(10)可以被写成如下形式：

∂C∂b=∂C∂aa(1−a)(11)\frac {\partial C}{\partial b}=\frac {\partial C}{\partial a}a(1-a) \tag{11}

将其代入式(9)的第二个式子中

∂C∂a=a−ya(1−a)(12)\frac{\partial C}{\partial a}=\frac{a-y}{a(1-a)} \tag{12}

对上式进行积分，就可以得到：

C=−[yln⁡a+(1−y)ln(1−a)]+constant(13)C=-[y\ln a + (1-y)ln(1-a)]+\text{constant} \tag{13}

其中constant是积分常量。这是一个单独的训练样本xx对代价函数的贡献。为了得到整个代价函数，我们需要对所有的训练样本进行平均，于是得到下式：

C=−1n∑x[yln⁡a+(1−y)ln(1−a)]+constant(14)C=-\frac 1 n \sum_x [y\ln a + (1-y)ln(1-a)]+\text{constant} \tag{14}

这里的常量就是所有单独的常量的平均。

以上便是对于交叉熵推导的全过程

avatar
文章
阅读
粉丝