在一个很大的数组中找到第n大的数
前言
这是一道某大厂的面试题,要求是要尽可能快,因此第一时间否定了先排序后取下标,这个花的时间肯定久。在面试的时候我回答的是一种和 数据流中的中位数 中处理方式差不多的做法:将两个堆的大小改成一个大小为 n ,一个大小为 length - n ,然后其他的事情就和中位数的这题一样
但我的这个回答面试官并不满意,并且问我,你觉得这个题目和找中位数的能一样吗?然后给我指了一条路:用 快速排序 就可以不全部排序即可获取第 n 大的数,虽然他没说具体怎么做,但我也是马上反应过来了,居然把它给忘了!(最后得到了面试官一个算法还需努力的评价)
题目
在一个非常大的乱序数组中,所有数字都是不重复的,问如何以最快的时间找到第 n 大的数
思考
这里先讲一下我在面试过程中想到的 用两个堆实现 的方法,在面试结束后我就动手去实现了一遍,这个方法我就不过多的分析了,大致流程是这样子:
- 设置两个堆,一个大顶堆
A,一个小顶堆B - 在小顶堆
B长度不到n时,将当前数组元素放进大顶堆A,再将A堆顶元素取出放入B - 在小顶堆
B长度等于n时,将当前数组元素放进B,再将B堆顶元素取出放入A
后来发现只要一个小顶堆 B 就够了,没必要像 数据流中的中位数 这道题里用到两个堆,直接下面这段代码这样就好了:
// 将当前数组元素放进堆中
B.insert(num)
// 当堆的大小达到n时,弹出堆顶元素
if(B.size() == n) {
B.pop()
}
再仔细一想,这不就是用堆排序吗,还不是排完序再来找第几个的思想,确实如面试官所说的,这和找中位数的题能一样吗?而面试官所说的使用快速排序的方式,可以做到不用将整个数组排序,即可获取第 n 大的数字。具体是怎么做的,将会在下文中揭晓
解答
这里先梳理一下快速排序的思想及过程:
快速排序是一种基于 “分而治之” 的思想实现的排序方法,每一次都会选出一个元素作为 基准元素 ,通过与基准元素对比进行交换,大于基准的放一边,小于基准的放另一边,然后将数组以基准元素所在的位置进行分割,分割出来的两边再各自进行上述操作,直到最后分割出来的数组部分长度都为 1 时,数组就完成了排序
这里放一张动图来方便理解:
在这个排序的过程当中,每一次选出来的基准元素 ( 通常会选择当前分割的数组中的第一个 ) 在完成了交换之后,其实就已经处于排序后数组中的正确位置,因此可以通过判断基准元素的下标是否等于 n - 1 ,来获取数字中的第 n 大数字
具体的实现代码如下:
const getNthNum = (arr, n, start = 0, end = arr.length - 1) => {
if(start >= end) return arr[start]
const pivotIndex = partition(arr, start, end)
if(pivotIndex == n - 1) {
return arr[pivotIndex]
} else if(pivotIndex > n - 1) {
// 若当前基准元素的下标大于 n - 1,则继续往左边找
return getNthNum(arr, n, start, pivotIndex - 1)
} else {
// 若当前基准元素的下标大于 n - 1,则继续往右边找
return getNthNum(arr, n, pivotIndex + 1, end)
}
}
const partition = (arr, start, end) => {
let pivot = arr[start]
// 用于标记当前处于正确顺序的边界
let mark = start
for(let i = start + 1; i <= end; i++) {
if(arr[i] > pivot) {
// mark++相当于向外扩充边界
mark++
// 然后将本属于边界外的部分和新找到的正确元素交换
[arr[mark], arr[i]] = [arr[i], arr[mark]]
}
}
arr[start] = arr[mark]
arr[mark] = pivot
return mark
}
为了验证该方法确实比排序后获取元素的方式要来得快,我编写了一段用于简单测试的代码,下面是自动生成测试数据的部分:
// 洗牌算法,用于将生成的单调递增数组打乱顺序
Array.prototype.shuffle = function() {
var array = this;
var m = array.length,
t, i;
while (m) {
i = Math.floor(Math.random() * m--);
t = array[m];
array[m] = array[i];
array[i] = t;
}
return array;
}
// 使用keys()函数将20480大小的数组用0到20479按顺寻填充
const array = [...new Array(20480).keys()]
array.shuffle()
const n = parseInt(Math.random() * 10000)
接下来就是对比直接排序取下标、堆排序和快速排序三种方式各自所画的时间,由于 JS 自带的数组排序方法 Array.prototype.sort 是原生实现,自然会比我们手写的 JS 代码要来的快,因此这里的直接排序取下标用的是 JS 代码写的插入排序,只用于参考
运行的结果如下:
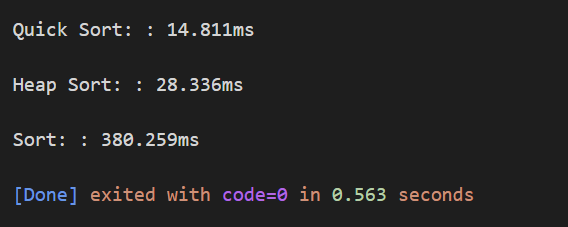
可以看出在数组长度为 20480 这么大时,插入排序的耗时与其余两者差距非常大,而快速排序差不多是堆排序的两倍快,因此可以认为快速排序为更优解(这里不敢说最优解,感觉可能会有更优的,如果有懂的大佬还请在评论区指点一二)