高等代数（上）

符号约定、用词约定

线性代数 符号约定、用词约定

$A$ : 矩阵 det(A) : 矩阵A的行列式, 为一实数 $E_{n}$ 或 $I_{n}$ : 单位阵，n行n列的单位方阵 $\mu_{k,i}$ : 矩阵的第k行第i列元素的余子阵，为一更小的矩阵

1.4 行列式

行列式 由余子阵递归定义

行列式的定义是递归定义

矩阵A是n行n列的方阵,
矩阵A中的第k行第i列元素记为$a_{k,i}$

矩阵A中去掉第k行和第i列 ，余下的元素组成的矩阵，称为原矩阵A的余子阵$\mu_{k,i}$

例如，将矩阵A按第一行元素的余子阵展开，则有 矩阵A的行列式det(A)定义为：

$det(A)=\sum_{i=1}^{n} a_{1,i}det(\mu_{1,i})$

可见，行列式定义显然是递归的: 矩阵A的行列式由多个更小的矩阵的行列式定义的， 这些更小的矩阵就是原矩阵A的余子阵。

显然， 可以将矩阵A按任一行的余子阵 展开，来定义矩阵A的行列式det(A), 如下：

$det(A)=\sum_{i=1}^{n} a_{k,i}det(\mu_{k,i}), {\forall}k \in \{1,2,...,n\}$

可以将矩阵A按任一列的余子阵 展开，来定义矩阵A的行列式det(A)，如下：

$det(A)=\sum_{k=1}^{n} a_{k,i}det(\mu_{k,i}), {\forall}i \in \{1,2,...,n\}$

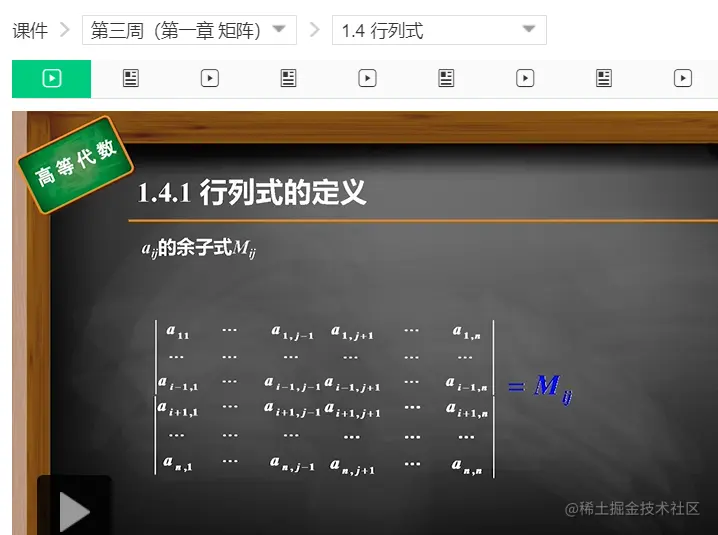
余子阵$\mu_{k,i}$的行列式$det(\mu_{k,i})$称为余子式 , 余子式$det(\mu_{k,i})$又记为$M_{k,i}$

不确定，线性代数教材中有没有余子阵的叫法，但有余子式。
但显然应该有余子阵的叫法，才是合理的。

伴随矩阵 中的每个元素都是余子式

伴随矩阵$A^{*}$ 中的每个元素都是余子式$det(\mu_{k,i})$

逆矩阵 的 行列式倍 为 伴随矩阵

逆矩阵$A^{-1}$ 为 $\dfrac{1}{det(A)}$ 倍 伴随矩阵$A^{*}$ 即 : $A^{*} * A=det(A) I_{n}$