原文链接
简介
近几十年来,推荐系统在电子商务的多个领域都很流行。然而,现有的大多数推荐系统设计都想当然地采用了以下两个假设:
- 未观察到的用户与项目之间的交互(即未标记的用户-项目元组)通常被标记为负样本;
- 观察到的用户-项目及其交互行为代表真实的相关性分布。
然而,这些假设对于现实世界的推荐系统通常是不成立的。
例如:在第一个假设中,假设如果𝑖与𝑢有交互,而𝑗没有交互,则项目𝑖对用户𝑢比项目𝑗更相关。这个假设并不一定是正确的,因为项目𝑗和用户𝑢之间缺少交互可能是因为项目𝑗和用户𝑢之间缺乏曝光,而不是𝑢对𝑗不感兴趣。也就是说:未标记的用户-项目对可能是正样本,也可能是负样本。因此,在训练过程中简单地将未标记元组作为负样本不可避免地会降低模型的性能。
基于这个情况,这篇文章开发了一个新框架,该框架通过训练一个无偏见的 positive-unlabeled(PU)鉴别器来区分真正相关的用户-项目对和不相关的用户项目对,还包括一个学习潜在用户-项目连续分布的生成器。框架中使用了生成对抗网络(GAN),GAN等生成式模型试图通过从隐式生成模型中学习底层数据分布来缓解负采样问题,提出了一种基于生成对抗网络的PU推荐方法(Positive-Unlabeled REcommendation, PURE)。
预备知识
问题定义
为研究隐式推荐问题,首先定义用户和项目的集合为U和I。对于用户u,他会和一系列项目进行交互,定义用户-项目交互矩阵为R∈{1,0}M×N,M,N为用户和项目的数量,若用户u和项目i之间有交互,则Rui=1。进一步,假设Ω为观察过实体的索引集合,即(u,i)∈Ω if Rui=1。注意,根据前面的描述可知:Rui=0 并不代表用户对该项目不敢兴趣。在实际中,每个用户只能评价和查看数量非常有限的项目。因此,在不丧失一般性的前提下,假设真正相关的用户-项目对在本质上是非常稀疏的。
综上,推荐问题通常表述如下:
给定: 一个用户集合U={u1,...,uM}、一个项目集合I={i1,...,iN},和观察到的用户-项目关系矩阵R
输出: 对于U中的每个用户U,估计其和未观察到项目的交互分数
广义矩阵分解
矩阵分解(Matrix Factorization, MF)是将用户-项目矩阵R分解为两个低维矩阵的乘积来实现隐因子模型(latent factor model)的一种推荐方法,MF模型通常将用户和项目映射到一个维数为d的联合隐因子空间。每个用户u和一个隐向量eu∈Rd相关联,每个项目i和一个隐向量ei∈Rd相关联。为学习这些向量,学习目标通常设计为:最小化观测到用户-项目对的平方误差:
eu,eimin(u,i)∈Ω∑(Rui−euTei)2
尽管MF在各种应用中取得了成功,但它假设用户和项目潜在特征在每个维度上都是同等重要的,并将它们与相等的权重结合在一起。然而,MF可能由于这种简单的假设而导致较大的排名误差。因此,使用GMF模型来提升MF的表达能力,上式修改为:
eu,eimin(u,i)∈Ω∪Ω−∑(Rui−{eu⊙ei}TrD)2
⊙为向量的乘积,Ω−为负样本的集合,从未观察到的用户-项目对交互中抽样得到。
rD为一个可学习的向量,用来建立eu到ei间的关系映射。
生成对抗网络 GAN
GAN由两个模型构成:鉴别器D和生成器G,二者一起玩一个极大极小博弈游戏。鉴别器D的目的是从生成器G中区分真实数据和假数据,同时生成器G致力于生成假数据用来尽可能混淆鉴别器D。
GAN的目标可以形式化为:
GminDmaxV(D,G)=Epdata(x)[logD(x)]+Epg(x)[flog(1−D(x))]
pdata(x),pg(x)为真实数据和由G生成的假数据的分布。GAN的目标等价于最小化pdata(x)和pg(x) 间的 Jensen-Shannon Divergence(JS散度)。
在实现过程中,GAN需要包含用于损失计算和梯度反向传播的目标函数,因此上述目标函数公式改写成:
GminDmaxV(D,G)=Epdata(x)[fD(D(x))]+Epg(x)[fG(D(x))]
fD,fG 为 D,G 的损失函数。
提出的方法
首先在PURE中提出了鉴别器,它能够在PU学习环境下考虑不同类型的训练样本,然后,引入了生成伪用户的生成器和通过覆盖特征空间的角落来增加模型表示能力的伪项目嵌入,PURE的架构总览如图1所示。
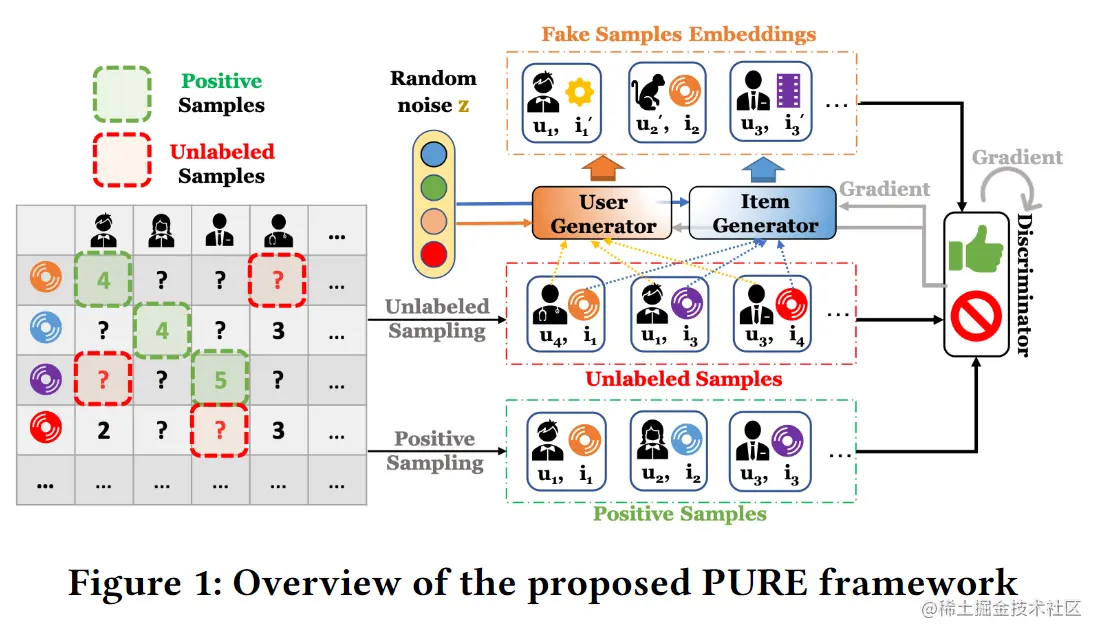
推荐中的PU分类
文章建议,将每个用户-项目对(u,i)映射为一个标量值,该值可以表示i到u的相关性。在架构中,设计鉴别器D(u,i)实现映射(u,i)到区间Y∈{0,1}中。鉴别器的目标是目区分给定用户真正相关的项目和不相关的项目,从直观上地说,D(u,i)只是一个输出概率关系评分的二元分类器,当项目确实与用户相关时,该输出得分应该是1;不相关时,该输出得分应该是0。形式化表示为:
D(u,i)=1+exp(−ϕ(u,i))1
ϕ(u,i):N×N→R为D(u,i)的决策函数,N为用户和项目索引的自然数集。
用pdata(u,i)表示用户和项目的潜在联合分布,用πp=p(Y=1)表示正类优先级(positive class prior)。根据总概率定律,将该联合分布改写为:
pdata(u,i)=πppp(u,i)+(1−πp)pn(u,i)
假设正用户-项目元组是从正边际分布pp(u,i)=PDATA(u,i∣Y=1)中抽取的,负元组是从负边际分布pn(x)=pdata(u,i∣Y=0)中抽取的。
为训练推荐模型,使用L(y^,y)作为损失函数,y为ground truth(可以理解为真值),y^为预测值。鉴别器的期望学习风险为R(D)=Epdata(u,i)[L(D(u,i),Y)],对于D,其正-负(PN)风险最小值学习可以写作:
DminR(D)=πpRp+(D)+(1−πp)Rn−(D)
Rp+(D)=Epp(u,i)[L(D(u,i),1)]为相关样本的风险关于正标签Y=1;Rn−(D)=Epn(u,i)[L(D(u,i),0)]为不相关样本的风险关于负标签Y=0。实际中Rp+(D)可以使用观测过的数据来近似,而Rn−(D)通常是未知的。为了估计学习风险,许多现有工作只是简单地假设来自未标记分布pu(u,i)的未观察到的用户-项目元组的集合是不相关的。然而,这种简单的假设在真实的世界中很难完全满足,因为这种“负”抽样数据中不可避免地会包含一定数量的正样本,因为未观察到的用户-项目元组不代表用户对此不感兴趣。
因此,为解决这个问题,PU学习通过将未观察到的用户-项目元组直接作为未标记样本来解决这个问题,并提供对应的理论保证。
将未标记边际分布写作:(1−πp)pn(u,i)=pu(u,i)−πppp(u,i),则Rn−(D)有以下等式:
(1−πp)Rn−(D)=Ru−(D)−πpRp−(D)
Ru−(D)=Epu(u,i)[L(D(u,i),0)]为关于负标签未标记样本的风险;Rp−(D)=Epp(u,i)[L(D(u,i),0)]为关于负标签正样本风险。
因此,最终最小化风险问题可以重写为:
DminR(D)=πpRp+(D)−πpRp−(D)+Ru−(D)
通过上述公式,鉴别器可以通过最小化pp(u,i),pu(u,i)的学习风险来区分用户-项目间的相关性。
鉴别模型
在明确了风险最小化目标的基础上,通过以下几组训练样本来经验性训练鉴别器:
从给定观察中得到的正样本
用户u和项目i在给定数据集中被观察到,并确定相关,即:Rui=1。对于这类样本,鉴别器的目标是最大化下面的目标:
V(D)1=(u,i)∈Ω∑npπplogD(u,i)−πplog(1−D(u,i))
其中np=∣R∣表示观测到的正元组的数量。
从未观测样本和生成器中得到的未标记样本
给定用户u,鉴别器需要给那些没有被排名或观看的项目分配较低的分数,从未观察到的样本和生成的用户-项目样本中分解出这部分目标样本:
V(D)2=(u,i)∈Ω−∑nulog(1−D(u,i))+[log(1−D(u,i′))+log(1−D(u′,i))]
假用户u′∼G()zu和假项目i′∼G(zi)由用户和项目生成器生成,nu为从未标记样本中抽取的未标记元组的数量。
生成模型
生成模型的目的是生成假样本,尽可能愚弄鉴别器。因此,对于一个真实样本(u,i),生成器Gi(zi)的任务是生成一个假项目i′让其尽可能与u相关,假项目可以是虚拟的,甚至不用存在于项目集合I中,类似的用户生成器的任务是生成假用户u′使其尽可能与i相关。特别的,将两个生成器的噪声设定为一个随机高斯噪声:
zi,zu∼N(0,δI)
噪声输入的均值将是一个零向量0,其大小和嵌入维数d相同。这里的I∈Rd×d为一个单位矩阵,其值由δ控制,表示生成器噪声输入的隐偏差。之后,使用一个多层感知器(multi-layer perceptron , MLP)用于生成假项目i′和用户u′,如下所示:
i′∼Gi(zi)=ReLU(Wi2⋅ReLU(Wi1⋅zi+bi1)+bi2) u′∼Gu(zu)=ReLU(Wu2⋅ReLU(Wu1⋅zu+bu1)+bu2)
显然其中的W,b表示权重和偏置。
综上所述,得到PURE的总体目标函数:
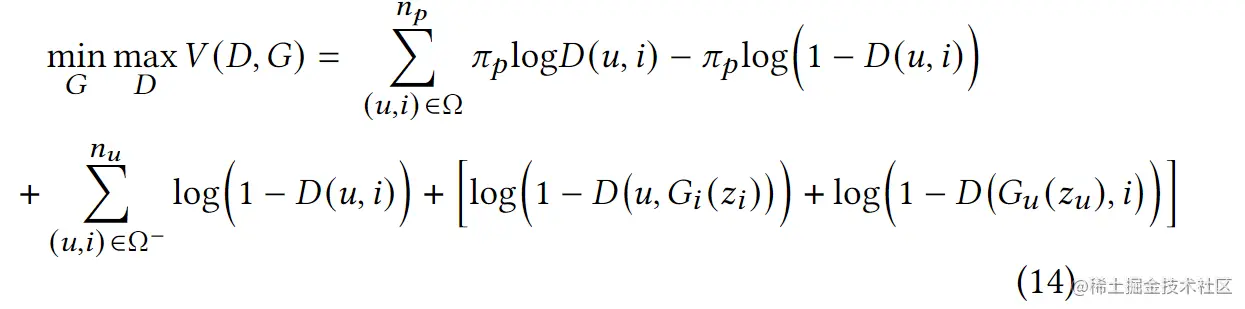
模型分析
鉴别器实例化
鉴别器的决策函数ϕ(u,i)可以有多种定义方法,在文章的实验中,是用来GMF的方法,假设用户和项目的嵌入是等维度的:
D(u,i)=1+exp(−{eu⊙ei}TrD)1
若扩展到用户和项目不等维度的情况,上面的公式可转化为:
D(u,i)=1+exp(−euTMDei)1
其中eu∈Rdu,ei∈Rdi,为两个不同维度的嵌入,MD∈Rdu×di为一个可学习到的关系映射矩阵。
抽样方式
在PN学习中,一种常见的做法是将观察到的用户-项目元组视为正样本,未观察到的的视为负样本。这种方法有显然的局限性,因此在PURE中,改用了UNS采样策略,因为未标记数据已经在PU学习目标中被明确建模。
算法
PURE的算法伪代码如下所示:
