【论文学习】VAM原文链接简介创意在电子商务中对于产品的展示有着非常重要的作用，卖家通常会为综合展示创造多个创意，因

简介

创意在电子商务中对于产品的展示有着非常重要的作用，卖家通常会为综合展示创造多个创意，因此展示最吸引人的设计来最大化点击率(CTR) 是至关重要的。然而，创意产品推荐比传统产品推荐更容易遭遇冷启动问题，因为用户点击数据更稀缺且创意也可能频繁地更改。在本文中提出了一种优雅的方法，将视觉先验知识整合到bandit model中，它基于一个叫做Neuralllinear 的框架，在汤普森抽样框架中考虑近似贝叶斯神经网络，利用神经网络的学习能力和后验抽样方法。总的来说，文章中：

提出一个视觉感知的排名模型(称为VAM)，它能够根据视觉外观来评估新创意
将学习到的视觉预测作为先验，提出了improved hybrid bandit model(HBM)，通过使用更多的观测数据来做出更好的后验估计
构造一个新的大型创造性数据集Creativerank，在该数据集和公共Mushroom数据集上进行了大量的实验，证明了该方法的有效性。

预备知识和相关工作

预备知识

问题描述

给定一个产品，目标是确定哪个创意是最有吸引力的。同时，需要估计预测的不确定性，确保在长期内获得最大的累积回报。在在线广告系统中，当一个广告展示给用户一个创意候选时，这个场景被认为是一种印象。

假设有 $N$ 个商品，定义为 $\{I^1,I^2,...,I^n,...,I^N\}$ ，每个商品 $I^n$ 由一组创意构成，写作 $\{C^n_1,...,C^n_m,...,C^n_M\}$ 。对于商品 $I^n$ ，学习目标是找到创意令：

C^n=\argmax_{c\in \{C^n_1,...,C^n_M\}} CTR(c)

此处的 $CTR()$ 表示该创意的点击率。

生成CTR的一种方式是累加近期点击数和印象数，并计算其点击率：

\hat{CTR}(C^n_m)=\frac{click(C^n_m)}{impression(C^n_m)}

$click(),impression()$ 表示创意 $C^n_m$ 的点击数和印象数。

这种计算方法存在一个问题：可能缺乏足够的印象数，特别是对一些冷启动的创意。

另一种方法是从历史数据中的上下文数据（例如图像内容等）中学习一个预测函数 $N()$ ，令：

\hat{CTR}(C^n_m)=N(C^n_m)

$N()$ 的输入为 $C^n_m$ ,从历史数据中学习，收集到的顺序数据可以表示为：

D=\{(C_1,y_1),...,(C_t,y_t),...,(C_{|D|},y_{|D|})\}

$y_t \in \{0,1\}$ 为便签，表示该创意是否被点击。

数据集构建

文章贡献一个大规模的创造数据集，它由创意图像和序列印象数据组成，可用于评价视觉预测和 exploration-exploitation（E&E）策略。

在2020年7月1日至2020年8月1日期间，从阿里巴巴展示广告平台收集大量多样的创意素材，印象总数约为2.15亿，有500827种产品和1707733个广告创意。

随机的日志策略 在线系统采用随机日志记录策略，随机绘制创意，以收集无偏数据集，Bandit 算法通过交互数据学习策略。

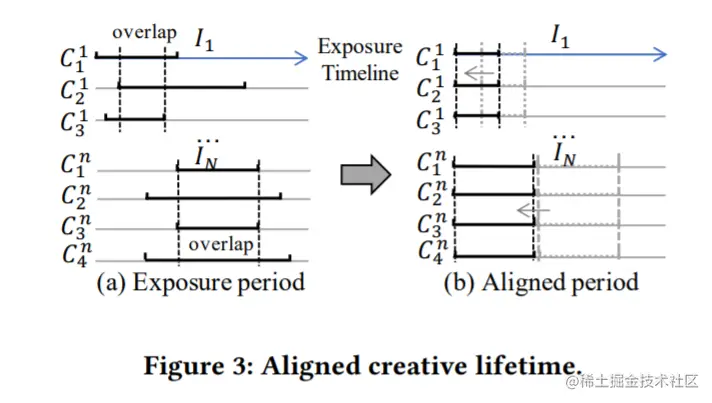
对齐创意生命周期 由于在线环境的复杂性，同样的创意在不同时期的CTRs是不同的，创意会被重新设计或删除，这将导致曝光时间不一致(如图3(a))。为了避免不同时间间隔带来的噪声，只收集候选创意之间的重叠周期(见图3 (b))，重叠时间在5 - 14天，涵盖了从冷启动到相对稳定阶段的创作生命周期。

Train/Validation/Test 数据分割 将500,827个产品随机分为300,242个培训样本、100,240个验证样本和100,345个测试样本，分别包含1,026,378/340,449/340,906个创意样本。

研究内容

设计总览

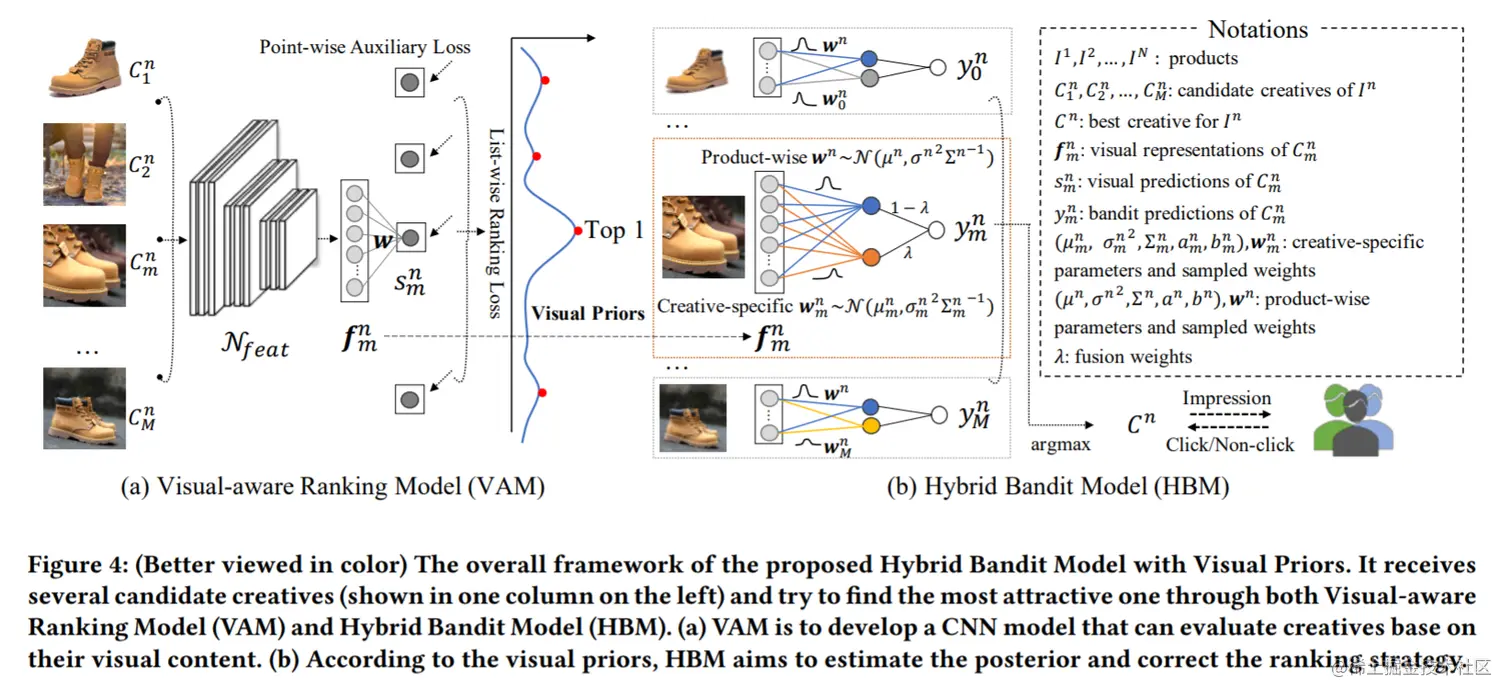
文中提出的具有视觉先验的混合Bandit Model的总体框架如图4所示，在图4（a）中，特征提取网络 $N_{feat}$ 同时输入一个商品的多种创意，并输出 $d$ 维中间特征 $\{f^n_1,...,f^n_m,...,f^n_M\}$ ，然后使用一个全连接层来计算其得分 $\{s^n_1,...,s^n+m,...,s^n_M\}$ 。

然后引入基于列表的排名损失（list-wise ranking loss）和辅助回归损失（auxiliary regression loss）来指导学习过程，这样的多目标优化帮助模型不仅关注创意排名，而且考虑到CTR的数值范围，这有利于接下来的Bandit Model。此外，由于数据噪声是现实应用程序中常见的问题，文中提供了几种实用的解决方案来减轻偶然的和恶意的噪声。经过以上步骤，模型可以直接通过其视觉内容来评价创意质量，即使是一个没有任何历史信息的新上传的作品。

之后使用HBM将学习到的 $f^n_m$ 合并为上下文信息，并通过与在线观察互动来更新学习策略，如图4(b)所示，混合模型结合了产品预测和创意预测，对于复杂的工业数据更加灵活。

VAM: Visual-aware Ranking Model

对于商品 $I^n$ ，使用特征提取网络 $N_{feat}$ 来提取创意的高层视觉表示，使用一个线性层来生成第 $n$ 个商品的第 $m$ 个创意的吸引力得分：

f^n_m=N_{feat}(C^n_m)\\ \ \\ s^n_m=f^{nT}_mw

此处 $w$ 表示线性层的学习参数。

基于列表的排名损失

为了学习创造性的相对顺序，需要将预测分数列表和 ground-truth CTRs分别映射到一个排列概率分布（permutation probability distribution），然后将这些分布之间的度量作为损失函数，映射策略和评估指标应该保证分数越高的候选创意排名越高。

排列概率和前 $k$ 个排名的定义见链接论文。受此启发，文中将创意排在前1位的概率简化为：

p^n_m=\frac{exp(s^n_m)}{\sum^M_{i=1}exp(s^n_i)}

基于top-1概率的指数函数既是尺度不变的，也是平移不变的，其对应的标签是:

y_{rank}(C^n_m)=\frac{exp(CTR(C^n_m),T)}{\sum^M_{i=1}exp(CTR(C^n_i),T)}

$exp(\cdot,T)$ 为一个带温度 $T$ 的指数函数，由于 $CTR(C^n_m)$ 是一个比较小的分数，因此使用 $T$ 来调整其尺度令top-1的样本的概率接近于1。

使用交叉熵作为度量，则商品 $I^n$ 的损失值为：

\mathcal{L}^n_{rank}=-\sum_{m}y_{rank}(C^n_m)\log(p^n_m)

通过这样的目标函数，模型着重于比较同一产品中的创意，它专注于top-1概率，因为它与真实场景一致，每个印象中只会展示一个创意。

基于点的辅助回归损失

排名损失函数只限制输出的顺序，不限制输出的数值尺度，因此添加了逐点回归（point-wise regression）作为正则化器：

\mathcal{L}^n_{reg}=\sum_m||CTR(C^n_m)-s^n_m||_2

$|| \cdot||$ 表示L2-范数。

最终的损失值由上述两个损失相加而成：

\mathcal{L}^n=\mathcal{L}^n_{rank}+\gamma\mathcal{L}^n_{reg}

文中 $\gamma =0.5$ 。

降低噪声

为避免噪声影响，VAM通过下面两种方式处理数据。

标签平滑（label smoothing）：一种经验贝叶斯方法，用于平滑CTR估计值。假设点击数服从二项分布，CTR服从一个先验分布：

click(C^n_m) \sim binomial(Impression(C^n_m),CTR(C^n_m))\\ \ \\ CTR(C^n_m)\sim Beta(\alpha,\beta)

$Beta(\alpha,\beta)$ 为CTRs的先验分布。

在观察到更多的点击后，通过二项分布和先验分布间的共轭性可以获得后验分布及平滑后的CTR $\hat{CTR}$ ：

\hat{CTR}(C^n_m)\frac{click(C^n_m)+\alpha}{impression(C^n_m)+\alpha+\beta}

其中 $\alpha,\beta$ 值可以使用历史数据用最大似然估计法计算。

加权抽样（weighted sampling）：一种训练过程的抽样策略。和平等对待每一个样本不一样，加权抽样更关注的是那些印象足够和CTRs更可靠的产品，方法为：

p^n=g(impression(I^n))

其中 $g()$ 表示取印象的对数， $p^n$ 表示商品 $I^n$ 的抽样权重。

HBM: Hybrid Bandit Model

HBM提供了一种优雅而有效的策略，利用视觉先验并通过混合Bandit 模型更新后验来解决E&E困境，在神经线性框架的基础上，对提取的视觉表示使用贝叶斯线性回归，假设在线反馈数据生成如下：

y=f^T\tilde{w}+\epsilon

$y$ 表示点击/没有点击的数据， $f$ 表示通过VAM提取出的视觉表示，此处需要学习 $\tilde{w}$ 的不确定性分布用来帮助提升E&E决策。 $\epsilon$ 是独立的等正态分布的随机变量，即：

\epsilon \sim \mathcal{N}(0,\sigma^2)

根据贝叶斯定理，若 $\tilde{w},\sigma^2$ 的先验分布与数据的似然函数共轭，则其后验概率分布可以被解析推导出来。然后使用后验抽样（也叫Thompson Sampling）来解决E&E困境，通过保持模型的后向性，并根据最优概率选择创意。 $\tilde{w},\sigma^2$ 的先验联合分布建模为：

\pi(\tilde{w},\sigma^2)=\pi(\tilde{w}|\sigma^2)\pi(\sigma^2)\\ \ \\ \sigma^2 \sim IG(a,b)\ and\ \tilde{w}|\sigma^2 \sim\mathcal{N}(\mu,\sigma^2\Sigma^{-1})

$IG()$ 为一个Inverse Gamma，其超参数设置为 $a_0=b_0=\eta>1$ 。 $\mathcal{N}()$ 为一个高斯分布带默认参数 $\Sigma_0=\lambda Id$ 。其中， $\mu_0$ 被设置为VAM中的学习权重 $w$ 。

基于一个共轭先验，其在时间 $t$ 的后验可以计算为：

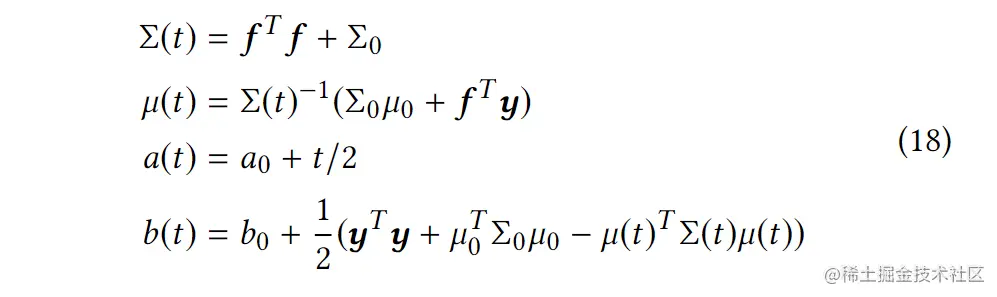
$f\in \mathbb{R}^{t\times d}$ 为一个包含之前印象上下文特征的矩阵， $y \in \mathbb{R}^{t\times 1}$ 为反馈奖励。在第 $t$ 个印象处更新上述参数后，得到了不确定性估计下的权重分布。从学习到的分布 $\mathcal{N}(\mu(t),\sigma(t)^2\Sigma(t)^{-1})$ 中得到 $w(t)$ ，并根据下面的公式选择商品 $I^n$ 的最优创意：

C^n=\argmax_{c\in\{C^n_1,...,C^n_M\}}(\mathcal{N}_{feat}(c)))^Tw(t)

上面的模型是所有产品的权重分布。这种简单的线性假设适用于小型数据集，但在处理工业数据时就不那么管用了。例如，鲜艳鲜艳的颜色在女性上衣上更有吸引力，而简洁的颜色更适合3C数码配件。除了这个产品方面的特性外，创意可能包含一个独特的设计属性，而这个属性不是通过共享权重来表达的，因此，VAM需要拥有同时包含共享和非共享的权重。

为实现这点，扩展之前的公式结合了产品感知和特定创意的线性项，对于创意 $C^n_m$ ，其线性回归方程可以改写为：

y^n_m=f^{nT}_mw^n+f^{nT}_mw^n_m

$w^n,w^n_m$ 为产品感知和特定创意的参数，它们被公式18优化。此外，VAM提出了一种融合策略，以自适应地结合这两个项，而不是简单的加法，如下所示：

y^n_m=(1-\lambda) f^{nT}_mw^n+\lambda f^{nT}_mw^n_m

$\lambda=1+exp(\frac{-impression(I^n+\theta_2)}{\theta_1})$ ，这是一个sigmoid函数带有调节参数 $\theta_1$ 和偏移 $\theta_2$ 。

上述过程如算法1所示：

实验

度量方法

Cumulative regret 常用于评估bandit model，其定义为：

Regret=E[r^*-r]

此处 $r^*$ 为最优策略的累积奖励，例如在特定环境下，总是选择具有最高预期回报的行为的策略。具体来说，VAM为其数据集选择最优的创意并计算 Regret为：

Regret=\frac{\sum^N_{n=1}click(C^n)}{\sum^N_{n=1}impression(C^n)}-sCTR

其中 $sCTR$ 的计算方法如算法2所示：