二叉搜索树(Binary Search Tree).
AVL树(艾薇儿树).
之前我们了解的树,都是一个节点可有多个孩子,但是它自身只能存储一个元素。二叉树限制更多,节点最多只能有两个孩子。一个节点只能存储一个元素,在元素非常多的时候,就是的要么树的深度非常大(树的高度非常大),这就使得内存存储次数非常多。
试想一下,为了要在一个拥有几十万个文件的磁盘中查找一个文本文件,你设计的算法需要读取磁盘上万次,还是读取几十次,这是有本质差异的。此时,为了降低对外存储设备的访问次数,就需要更好的数据结构来处理这样的问题。为此,引入了B树(多路查找树) 的概念。
B树是一种平衡的多路搜索树,多用于文件系统、数据库的实现。
我们先来看几个B树的样子,如下图所示:
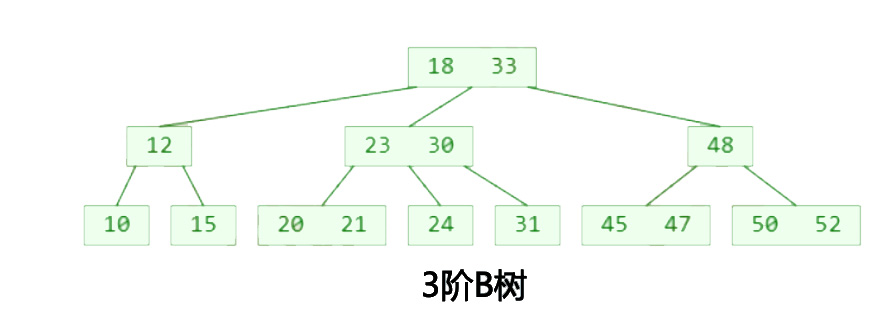
2-3.jpg
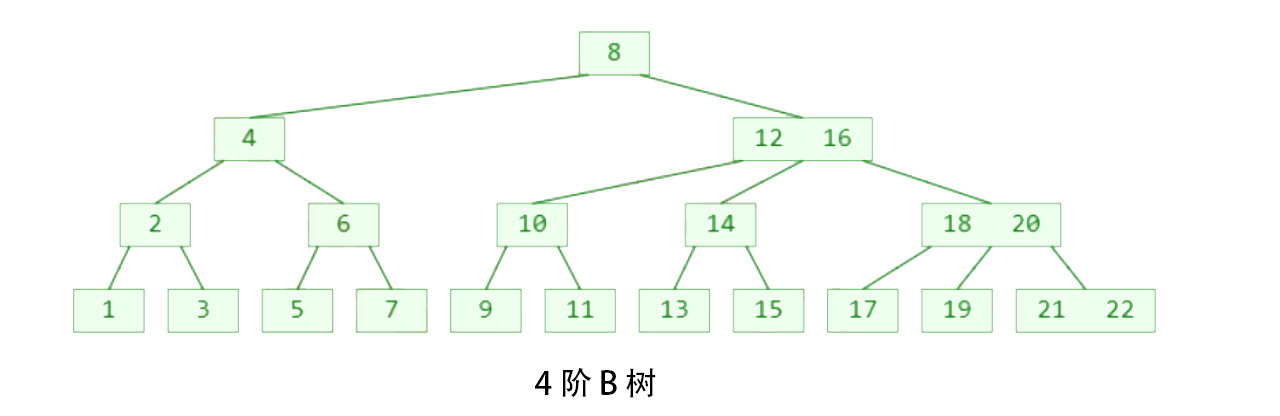
2-3-4.jpg
一、 ★★★【B树】性质:
◼假设一个节点存储的元素个数为 x
◼根节点:1 ≤ x ≤ m − 1
◼非根节点:┌ m/2 ┐ − 1 ≤ x ≤ m − 1
◼如果有子节点,子节点个数 y = x + 1
✓根节点:2 ≤ y ≤ m
✓非根节点:┌ m/2 ┐ ≤ y ≤ m
☆★☆
假如3阶B数:
根节点:1 ≤ x ≤2
非根节点:┌ 3/2 ┐ − 1 ≤ x ≤ 3 − 1 ---> 1 ≤ x ≤ 2
如果有子节点,子节点个数 y = 3;
注意:①┌ ┐是向上取整,即代码中的Ceil()函数
②└ ┘是向下取整,即代码中的 Floor()函数
➢比如 m = 3,2 ≤ y ≤ 3,因此可以称为(2, 3)树、2-3树
➢比如 m = 4,2 ≤ y ≤ 4,因此可以称为(2, 4)树、2-3-4树
➢比如 m = 5,3 ≤ y ≤ 5,因此可以称为(3, 5)树
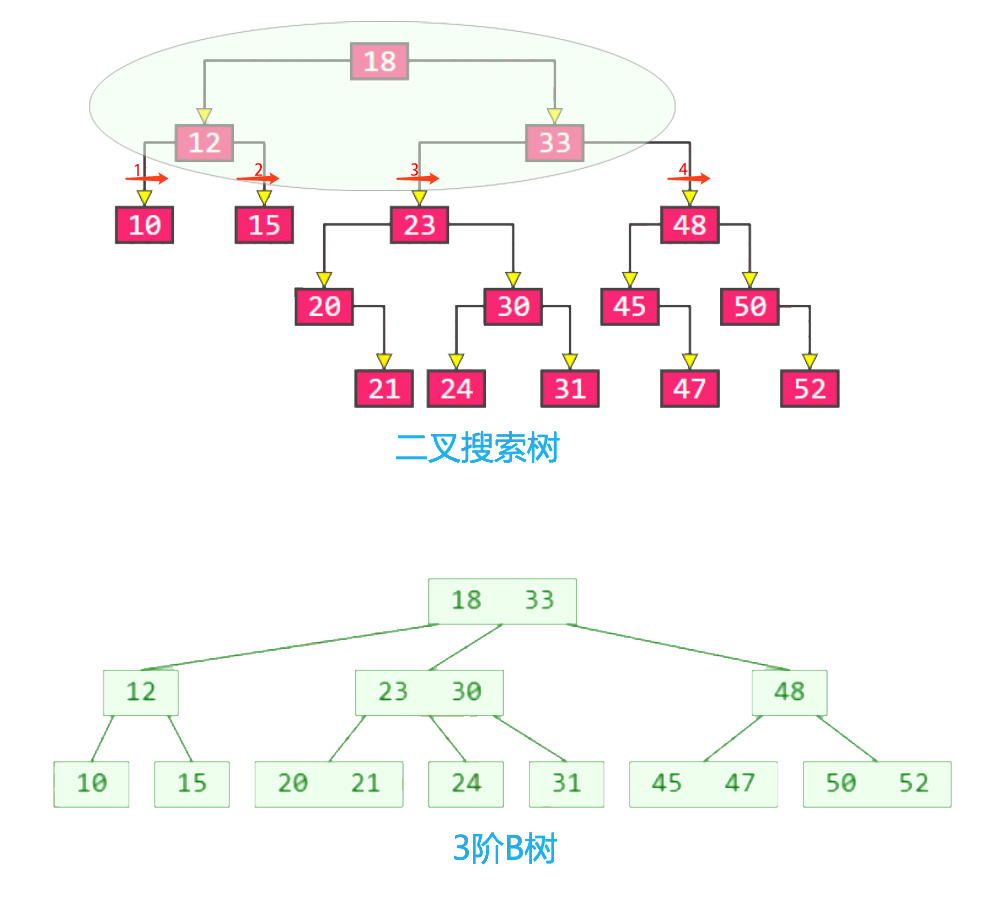
B树 VS 二叉搜索树
◼B树 和 二叉搜索树,在逻辑上是等价的
◼ 多代节点合并,可以获得一个超级节点
2代合并的超级节点,最多拥有 4 个子节点(至少是 4阶B树)
3代合并的超级节点,最多拥有 8 个子节点(至少是 8阶B树)
n代合并的超级节点,最多拥有 2n个子节点( 至少是 2n阶B树)
◼m阶B树,最多需要 log2m 代合并
01.jpg
二、【B树】节点的增加和删除
对于B树来说,与二叉搜索树相同,插入操作一定是发生在叶子节点上。可与二叉搜索树不同的是,B树插入一节点的过程可能会对该树的其余结构产生连锁反应。
1.节点添加步骤:
B树节点添加可分为两种情况
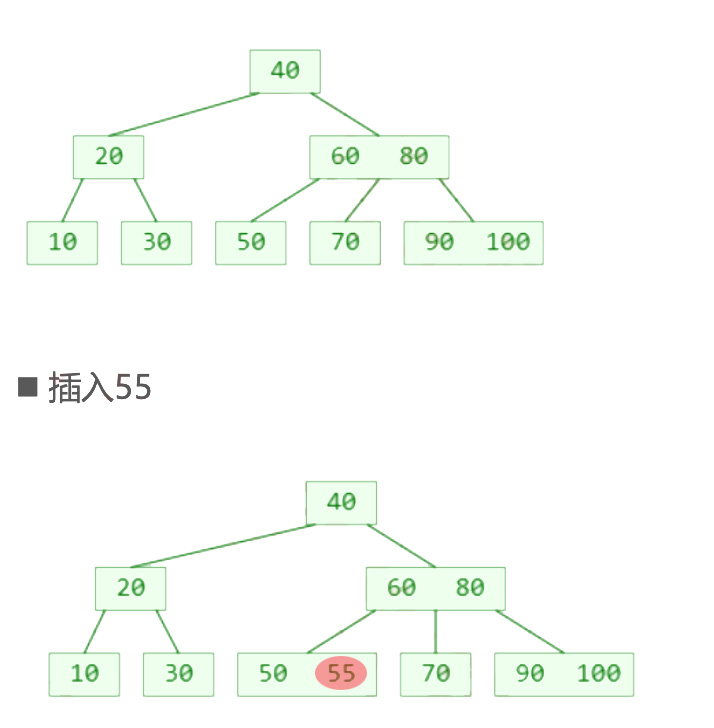
第一种情况:正常添加节点到对应的叶子节点上\
02.jpg
添加节点动画如下:
01.gif
第二种情况:添加节点上溢
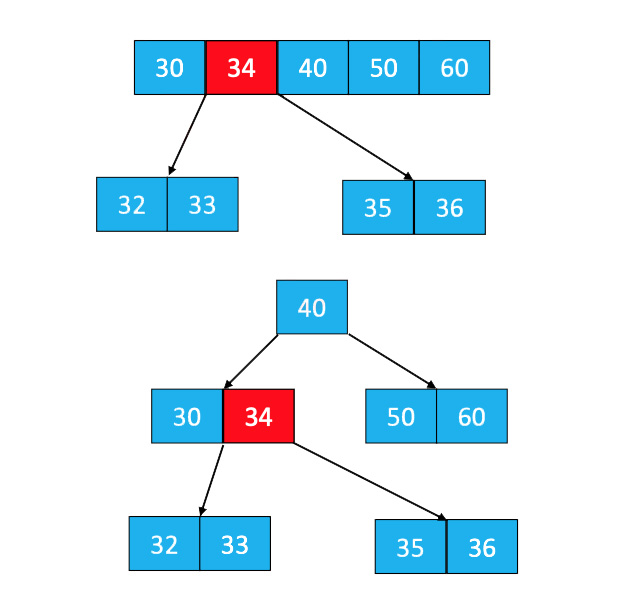
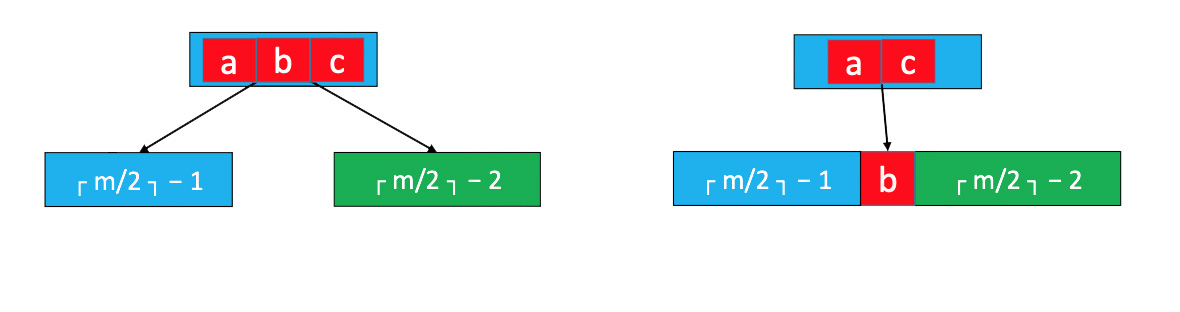
上溢节点的元素个数必然等于 m
◼假设上溢节点最中间元素的位置为 k
◼ 将 k 位置的元素向上与父节点合并
◼ 将 [0, k-1] 和 [k + 1, m - 1] 位置的元素分裂成 2 个子节点
上溢-分裂为两个节点.jpg
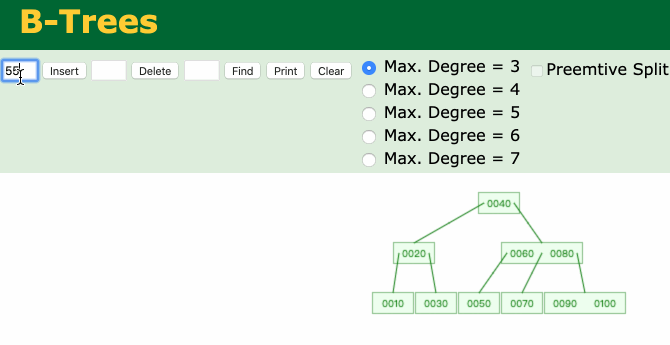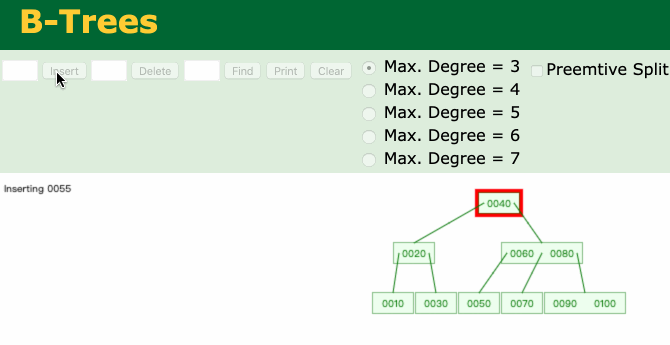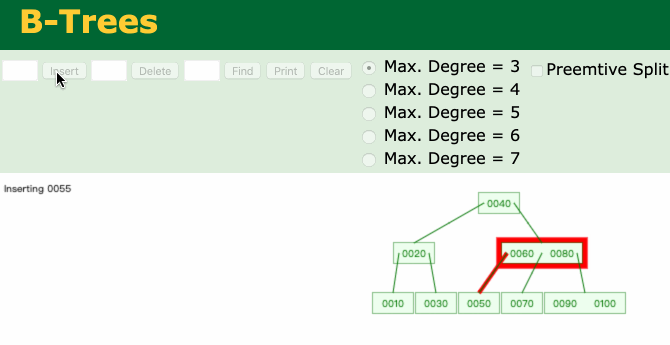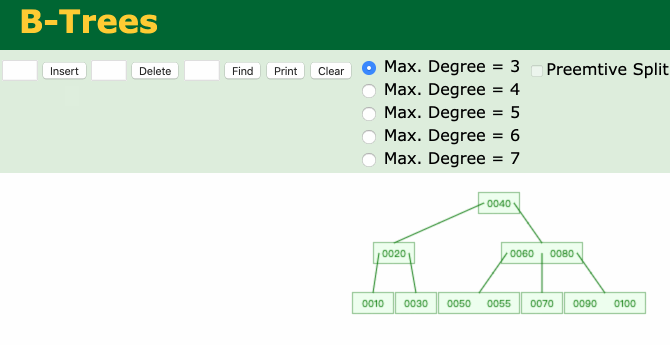
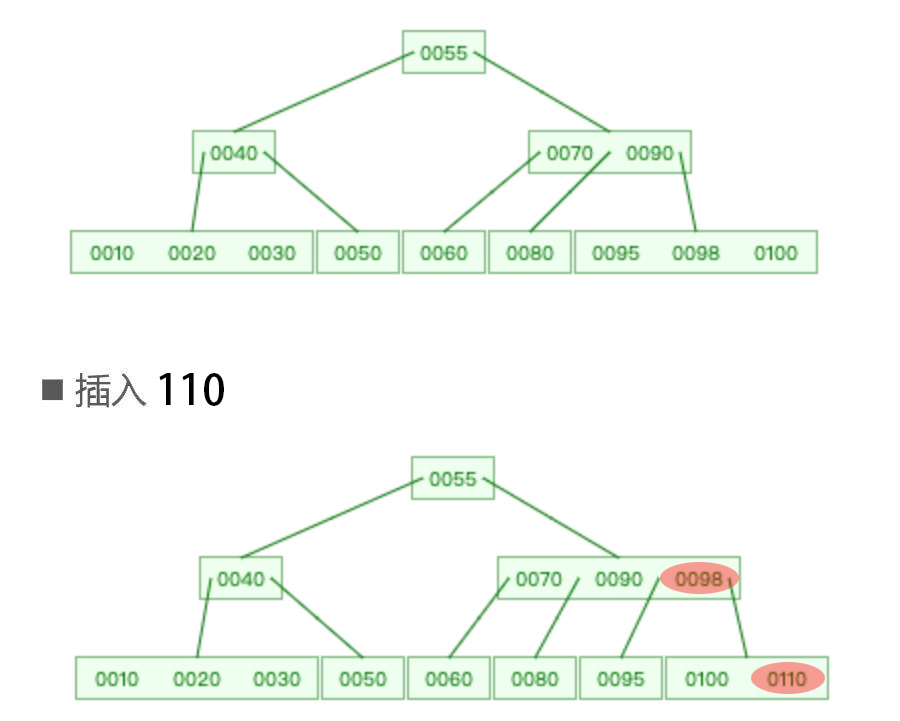
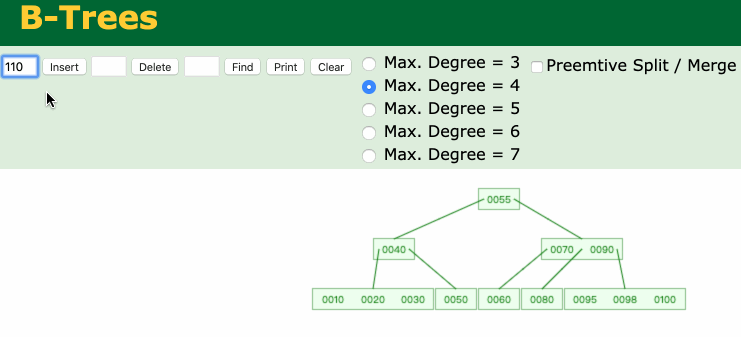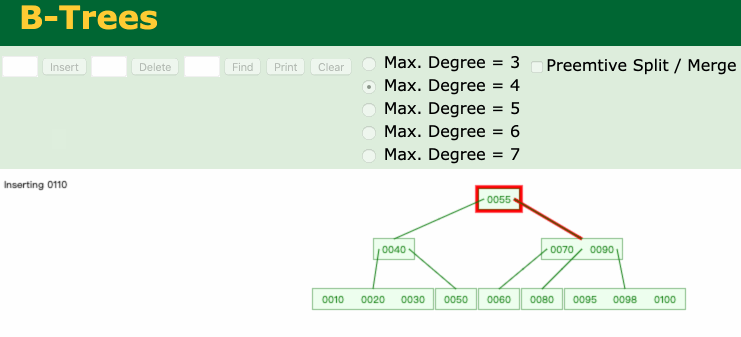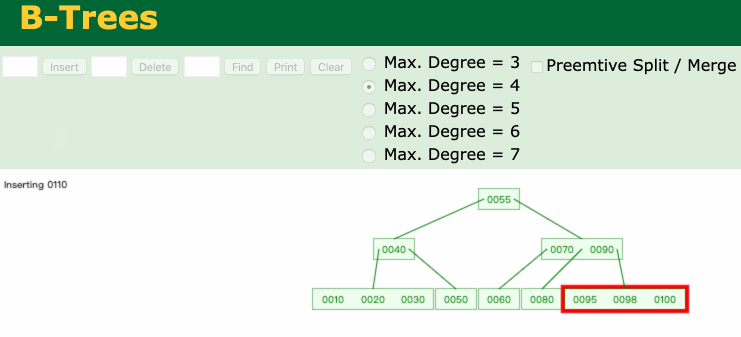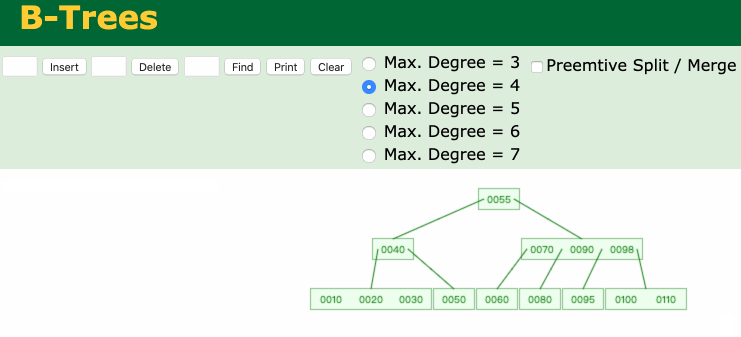
如下图所示,一个4阶B树,添加一个节点110,产生了上溢。
产生上溢的原因分析:
4阶B树需要满足以下条件:① 根节点:1 ≤ x ≤ 3(满足) ; ② 非根节点:1 ≤ x ≤ 3 (添加节点110后不满足,所以产生了上溢)\
03.jpg
添加节点动画如下:
02.gif
2.节点删除步骤:
B树节点删除也分为两种情况
第一种情况:删除叶子节点(4阶B树)\
04.jpg
删除节点动画如下:
03.gif
第二种情况:删除非叶子节点(包含节点下溢的情况)
◼1. 假如需要删除的元素在非叶子节点中
①. 先找到前驱或后继元素,覆盖所需删除元素的值
②. 再把前驱或后继元素删除
◼ 非叶子节点的前驱或后继元素,必定在叶子节点中
◼ 所以这里的删除前驱或后继元素 ,就是最开始提到的情况:删除的元素在叶子节点中
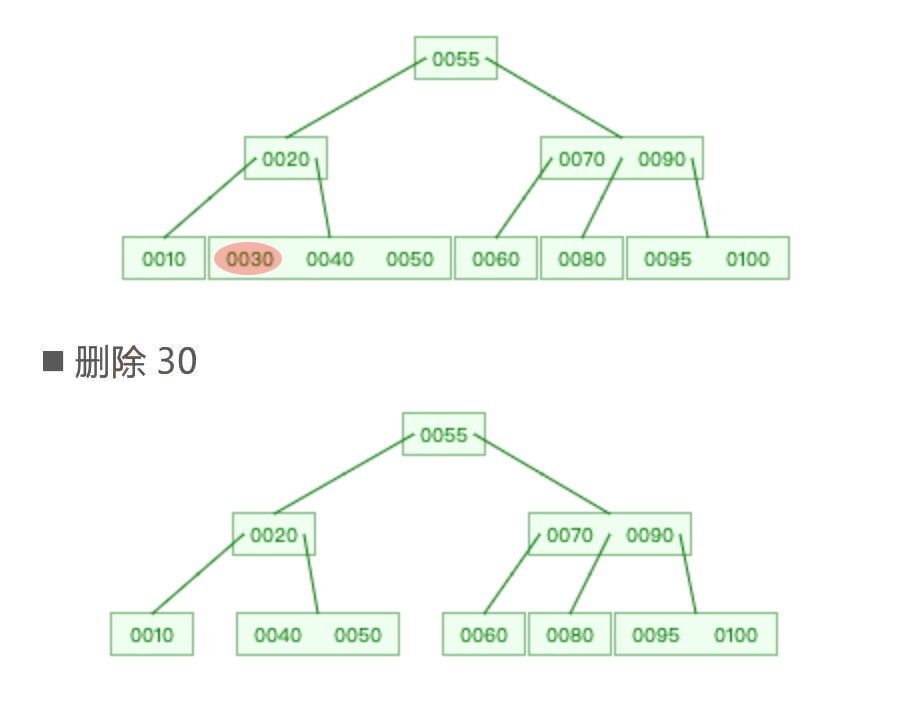
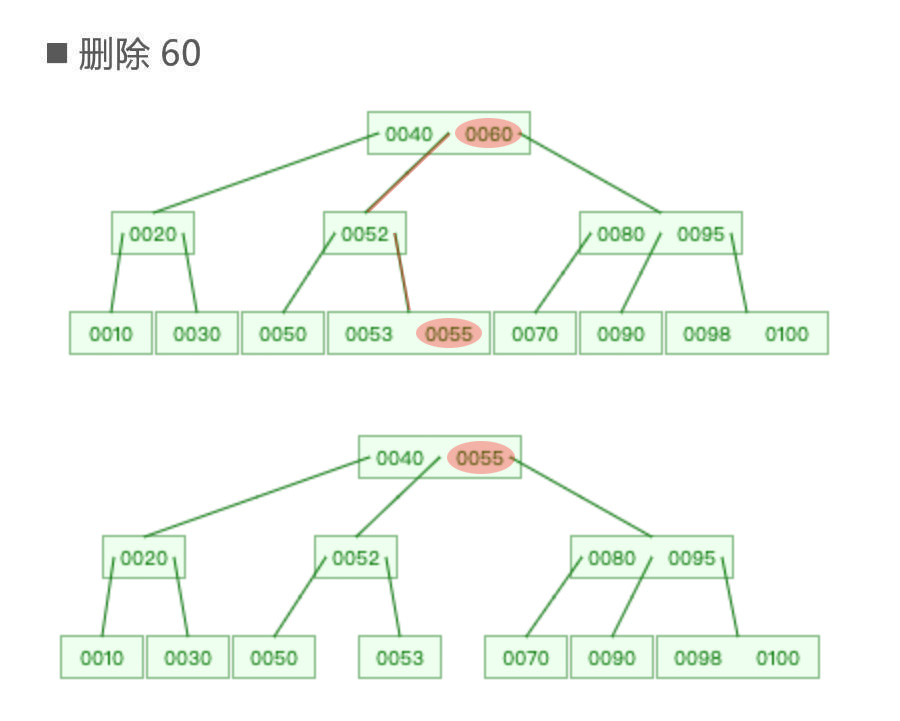
◼ 真正的删除元素都是发生在叶子节点中如下图所示,删除节点60,真正被删除的是60的前驱节点55。
05.jpg
删除节点动画如下:
04.gif
◼2. 假如需要删除的元素产生了下溢
下溢的解决分两种情况:(1).兄弟充足,兄弟节点可借 (2).兄弟节点不可借,父节点下来合并。
(1).兄弟充足,兄弟节点可借\
下溢-借兄弟节点.jpg
注意:这里不可以直接借用,即:不可以直接将A放到绿色的框中,因为B树叶满足二叉树的性质,左边小于右边,如果直接放过来,破坏了二叉树的性质。(2).兄弟节点不可借,父节点下来合并。
下溢-父节点合并.JPG
这个操作可能会导致父节点下溢,下溢现象可能会一直往上传播。
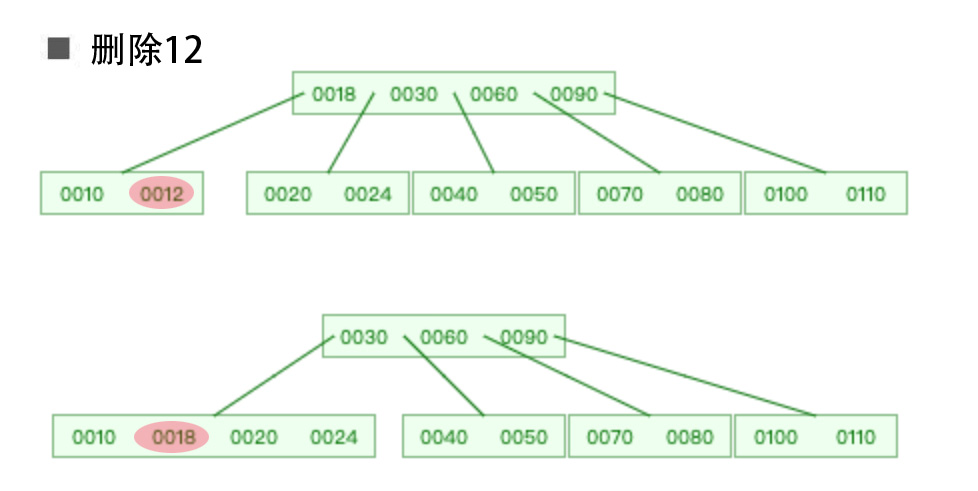
如下图所示,删除节点12,就产生了下溢。
产生下溢的原因分析:我们假定这是一棵5阶B树
5阶B树需要满足以下条件:① 根节点:1 ≤ x ≤ 4(满足) ; ② 非根节点:2 ≤ x ≤ 4 (删除节点12后不满足,所以产生了下溢)\
06.jpg
删除节点-父节点下来合并动画:\
05.gif
好了,B树学习告一段落,其实学习B树,最终是为了红黑树。
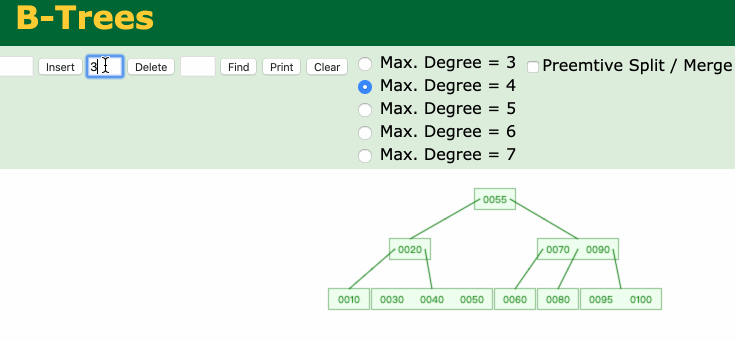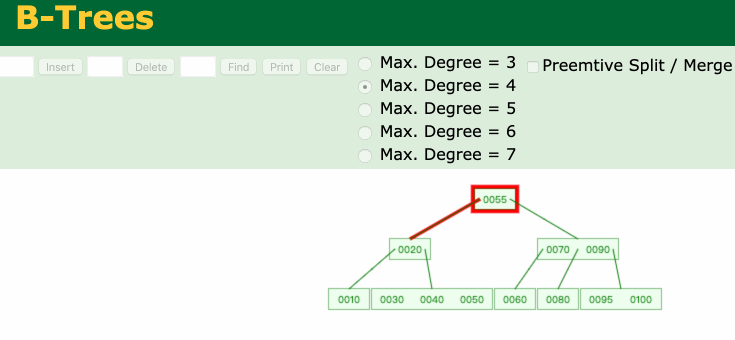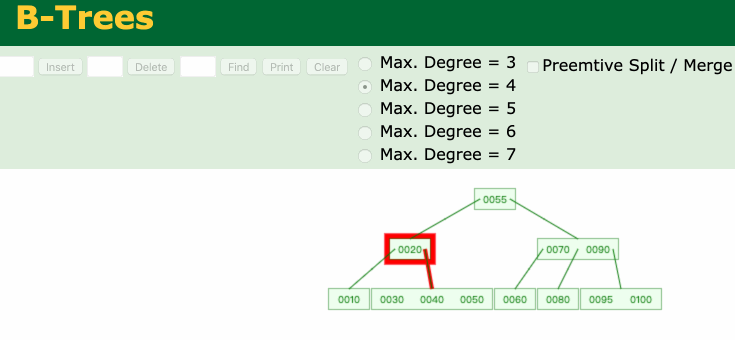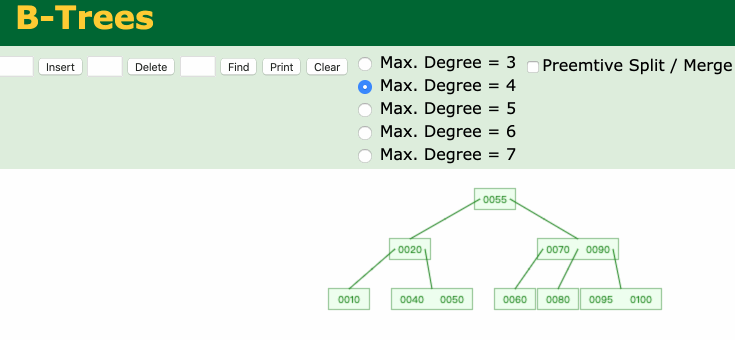
最后,推荐一个神奇的网站**Data Structure Visualizations**,可以帮助我们学习B树。