八大排序算法Java实现

冒泡排序

/*
 * 冒泡排序
 * 相邻元素比较，大的元素往后调
 */
public static void bubbleSort(int array[]){
	
	for(int i = array.length - 1 ; i >= 0 ; i--){
		
		boolean flag = false;     //设置一趟排序是否有交换的标识
		
		for(int j = 0 ; j < i ; j++){   //一趟冒泡排序
			
			if(array[j] > array[j+1]){
				swap(array, j, j+1);
				flag = true;    //标识发生了交换
			}
		}
		
		if(!flag)
			break;
	}
}

选择排序

/*
 * 选择排序
 * 每个位置选择当前元素最小的
 */
public static void selectSort(int array[]){
	
	
	for(int i = 0 ; i < array.length-1 ; i++){
		
		int minPosition = i;
		int min = array[i];
		
		for(int j = i+1 ; j <array.length ; j++){
			
			if(array[j] < min){
				min = array[j];
				minPosition = j;
			}
			
		}
		//若i不是当前元素最小的，则和找到的那个元素交换
		if(i !=  minPosition){
			array[minPosition] = array[i];
			array[i] = min;
		}
	}
}

插入排序

/*
 * 插入排序
 * 已经有序的小序列的基础上，一次插入一个元素
 */
public static void insertSort(int array[]){
	
	for(int i = 1 ; i < array.length ; i++){
		
		int current = array[i];   //待排元素
		
		int j = i;
		for(; j > 0 && array[j - 1] > current ; j--){
			//向前扫描，只要发现待排元素比较小，就插入
			
			array[j] = array[j - 1];    //移出空位
			
		}
		
		array[j] = current;    //元素插入
	}
}

快速排序

/*
 * 快速排序
 * 两个方向，左边的i下标一直往右走，当a[i] <= a[center_index]，
 * 其中center_index是中枢元素的数组下标，一般取为数组第0个元素。而右边的j下标一直往左走，当a[j] > a[center_index]
 * 如果i和j都走不动了，i <= j, 交换a[i]和a[j],重复上面的过程，直到i>j
 * 交换a[j]和a[center_index]，完成一趟快速排序
 * 枢轴采用三数取中法可以优化
 */
//递归快速排序
public static void quickSort(int a[]){
	qSort(a, 0, a.length - 1);
}
//非递归快速排序，手动利用栈来存储每次分块快排的起始点，栈非空时循环获取中轴入栈  
public static void quickSortNonRecursion(int array[]){
	 if (array == null || array.length == 1) return;
     //存放开始与结束索引
     Stack<Integer> s = new Stack<Integer>(); 
     //压栈       
     s.push(0); 
     s.push(array.length - 1); 
     //利用循环里实现
     while (!s.empty()) { 
         int right = s.pop(); 
         int left = s.pop(); 
         //如果最大索引小于等于左边索引，说明结束了
         if (right <= left) continue; 
                  
         int i = partition(array, left, right); 
         if (left < i - 1) {
             s.push(left);
             s.push(i - 1);
         } 
         if (i + 1 < right) {
             s.push(i+1);
             s.push(right);
         }
     } 
}
//递归排序，利用两路划分
public static void qSort(int a[],int low,int high){
	int pivot = 0;
	if(low < high){
		//将数组一分为二
		pivot = partition(a,low,high);
		//对第一部分进行递归排序
		qSort(a,low,pivot);
		//对第二部分进行递归排序
		qSort(a,pivot + 1,high);
	}
}
//partition函数
public static int partition(int a[],int low,int high){
	
	int pivotkey = a[low];   //选取第一个元素为枢轴记录
	while(low < high){
		//将比枢轴记录小的交换到低端
		while(low < high && a[high] >= pivotkey){
			high--;
		}
		//采用替换而不是交换的方式操作
        a[low] = a[high];
		//将比枢轴记录大的交换到高端
		while(low < high && a[low] <= pivotkey){
			low++;
		}
		a[high] = a[low];
	}
	//枢纽所在位置赋值
	a[low] = pivotkey;
	//返回枢纽所在的位置
	return low;
}

归并排序

/*
 * 归并排序
 * 把序列递归地分成短序列
 * 递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),
 * 然后把各个有序的短序列合并成一个有序的长序列，不断合并直到原序列全部排好序
 */
//将有二个有序数列a[first...mid]和a[mid+1...last]合并。  
public static void merge(int a[], int first, int mid, int last, int temp[]){
	
	int i = first,j = mid+1;
	int k = 0;
	
	while(i <= mid && j<= last){
		if(a[i]<a[j])
			temp[k++] = a[i++];
		else
			temp[k++] = a[j++];
	}
	
	while(i <= mid)
		temp[k++] = a[i++];
	while(j <= last)
		temp[k++] = a[j++];
	
	for(i = 0 ; i < k ; i++)
		a[first+i] = temp[i];
}

//递归合并排序
public static void mSort(int a[], int first,int last, int temp[]){
	if(first < last){
		int mid = (first + last) / 2;
		mSort(a, first, mid, temp);
		mSort(a, mid+1, last, temp);
		merge(a, first, mid, last, temp);
		
	}
}
//提供通用归并排序接口
public static void mergeSort(int a[]){
	int[] temp = new int[a.length];
	mSort(a, 0, a.length-1, temp);
}

希尔排序

/*
 * 希尔排序
 * 按照不同步长对元素进行插入排序
 * 插入排序的一种
 */
public static void shellSort(int a[]){
	if(a == null || a.length == 0){
		return;
	}
	int len = a.length;
	//初始化增量
	int inc = len;
	do{
		//增量变化规则
		inc = inc / 3 + 1;
		for(int i = inc; i < len; i++){
			//待排元素
			int cur = a[i];
			int j = i;
			//向前扫描，只要发现待排元素比较小，就插入
			for(; j >= inc && a[j - inc] > cur; j -= inc){
				//移除空位
				a[j] = a[j - inc];
			}
			//元素插入
			a[j] = cur;
			
		}
	}while(inc > 1);
}

堆排序

/*
 * 堆排序
 * 调整最大堆，交换根元素和最后一个元素。
 * 参数说明：
 *     a -- 待排序的数组
 */
public static void heapSort(int[] a) {
	if(a == null || a.length == 0){
		return;
	}
	int len = a.length;
	//从尾部开始，调整成最大堆
	for(int i = len / 2 - 1; i >= 0; i--){
		maxHeapDown(a, i, len - 1);
	}
	
	//从最后一个元素开始对序列进行调整，不断缩小调整的范围直到第一个元素
	for(int i = len - 1; i >= 0; i--){
		//交换a[0]和a[i]。交换后，a[i]是a[0..i]中最大
		int tmp = a[0];
		a[0] = a[i];
		a[i] = tmp;
		//调整a[0..i - 1]，使得a[0..i - 1]仍然是一个最大堆
		maxHeapDown(a, 0, i - 1);
	}
}

/*
 * 注：数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
 *     其中，N为数组下标索引值，如数组中第1个数对应的N为0。
 *
 * 参数说明：
 *     a -- 待排序的数组
 *     lo -- 被下调节点的起始位置(一般为0，表示从第1个开始)
 *     hi   -- 截至范围(一般为数组中最后一个元素的索引)
 */
private static void maxHeapDown(int[] a, int lo, int hi){
	//记录当前结点位置
	int curIndex = lo;
	//记录左孩子结点
	int left = 2 * curIndex + 1;
	//记录当前结点的值
	int curVal = a[curIndex];
	
	//保证curIndex,leftIndex,rightIndex中，curIndex对应的值最大
	for(; left <= hi; curIndex = left, left = 2 * left + 1){
		//左右孩子中选择较大者
		if(left < hi && a[left] < a[left + 1]){
			left++;
		}
		if(curVal >= a[left]){
			break;
		}else{
			a[curIndex] = a[left];
			a[left] = curVal;
		}
	}
}

基数排序

/*
 * 基数排序
 * 按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位
 */
public  static void radixSort(int[] array,int d)
{
    int n=1;   //代表位数对应的数：1,10,100...
    int k=0;   //保存每一位排序后的结果用于下一位的排序输入
    int length=array.length;
    int[][] bucket=new int[10][length];      //排序桶用于保存每次排序后的结果，这一位上排序结果相同的数字放在同一个桶里
    int[] order=new int[length];    //用于保存每个桶里有多少个数字
    while(n<d)
    {
        for(int num:array)    //将数组array里的每个数字放在相应的桶里
        {
            int digit=(num/n)%10;
            bucket[digit][order[digit]]=num;
            order[digit]++;
        }
        for(int i=0;i<length;i++)      //将前一个循环生成的桶里的数据覆盖到原数组中用于保存这一位的排序结果
        {
            if(order[i]!=0)        //这个桶里有数据，从上到下遍历这个桶并将数据保存到原数组中
            {
                for(int j=0;j<order[i];j++)
                {
                    array[k]=bucket[i][j];
                    k++;
                }
            }
            order[i]=0;      //将桶里计数器置0，用于下一次位排序
        }
        n*=10;
        k=0;               //将k置0，用于下一轮保存位排序结果
    }
    
}

通用的swap函数

public static void swap(int array[],int i,int j){
	int temp = array[i];
	array[i] = array[j];
	array[j] = temp;
}

总结

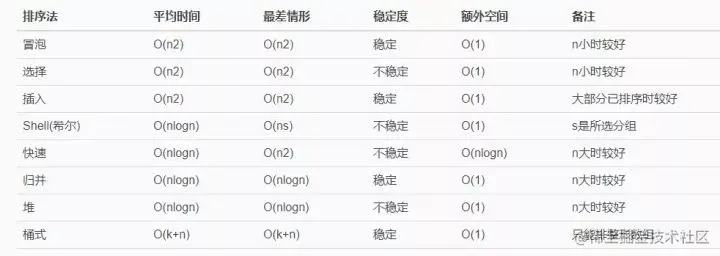
• 下面是一个总的表格，大致总结了我们常见的所有的排序算法的特点。

• 性能测试