神经网络学习笔记4——softmax层+对数代价函数这是我参与11月更文挑战的第8天除了交叉熵方法外，还有一种改进神经

这是我参与11月更文挑战的第8天

除了交叉熵方法外，还有一种改进神经网络的方法——添加柔性最大值（softmax）神经元层

softmax神经元层

softmax神经元层为神经网络定义一种新的输出层，其在神经网络中的位置如下图所示：

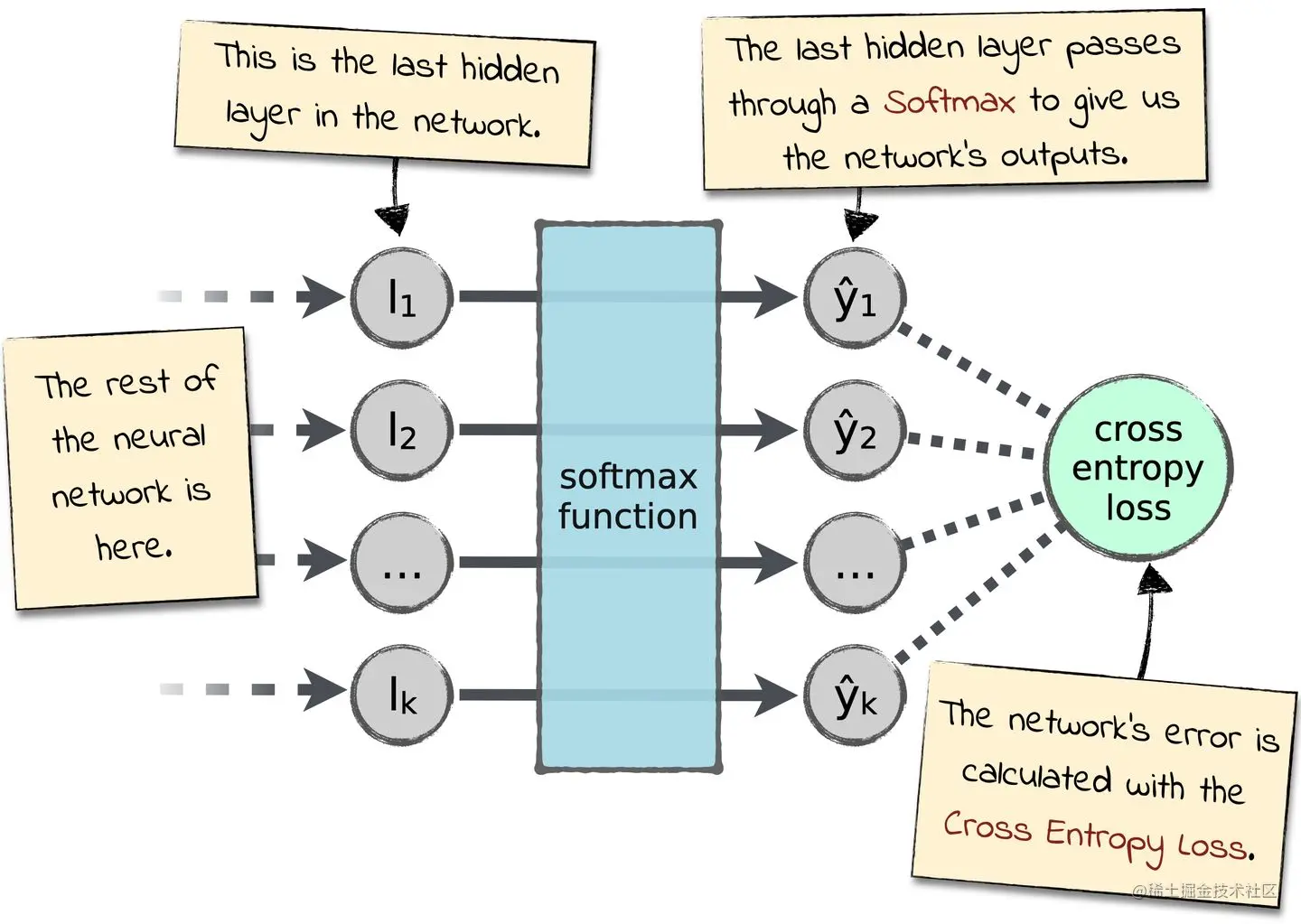
对于输入 $z^L_j=\sum_kw^L_{jk}a^{L-1}_k+b^L_j$ ，softmaxt方法应用softmax函数在 $z^L_j$ 上，即对于第 $j$ 个神经元其激活值为：

a^L_j=\frac{e^{z^L_j}}{\sum_ke^{z^L_k}}

$\sum_k$ 表示在所有神经元上求和，通过公式可知softmax函数会对神经元输入值做两个操作：

将输入中间值 $z^L_j$ 通过指数函数 $e^x$ 映射到一个 $[0,+\infty]$ 的空间中
出非负区间上，求出每个神经元映射值占在所有值之和的比例

根据上面公式推断，所有神经元输出激活值的和应该为1，即：

\sum_j a^L_j=\frac{\sum_j e^{z^L_j}}{\sum_ke^{z^L_k}} = 1

也就是说，softmax层的输出可以被看做是⼀个概率分布，在很多问题中可以直接将输出激活值 $a^L_j$ 解释为输入样本属于某分类的概率，这对于解决问题是一种很方便的做法。

softmaxt函数

S_i=\frac{e^i}{\sum_je^j}

softmax提升学习速率的原理

为解释这一点，首先定义一个对数似然（log-likelidood）代价函数（它是softmax层很好的搭档）， $x$ 表示神经网络的训练输入， $y$ 表示期望目标输出，则关于 $x$ 的对数似然代价函数为：

C=-\ln a^L_y

计算代价函数关于参数 $w$ 和 $b$ 的偏导（计算过程）：

\frac{\partial C}{\partial b^L_j}={a^L_j-y_j}

\frac{\partial C}{\partial w^L_{jk}}=a^{L-1}_j(a^L_j-y_j)

这种方法同样排除了 $\sigma'(z)$ 的影响，避免了学习速率下降问题。因此“softmax+对数似然代价函数”的小效果可以等同于：“二次代价函数+交叉熵损失”

为什么要叫softmax

给softmax函数增加一个正常数量 $c$ ，公式变为：

a^L_j=\frac{e^{cz^L_j}}{\sum_ke^{cz^L_k}}

从之前解释过公式的含义中可知，增加 $c$ 之后所有输出激活值的和依旧是1。当 $c=1$ 时得到softmax函数，当 $c\rightarrow +\infty$ 时， $a^L_j\rightarrow 1$ ，这就导致无法区分每个类别概率区别， $soft$ 的含义即将概率分布曲线变得平滑，让小的数字也有一定的值。

而 $max$ 的含义更容易理解，从 $e^x$ 函数图像中可以看出它增长极快，可以将大的数映射到很大的空间，小的数映射为比较小的空间，有效实现筛选最大概率的目的。

softmax和对数似然的反向传播

在反向传播算法中要计算误差 $\delta$ ，在softmax+对数似然的反向传播算法中其计算公式如下：

\delta^L_j=a^L_j-y_j

即 $\frac{\partial C}{\partial b^L_j}$ 的值为 $\delta^L_j$ ，证明过程在之前的笔记中已经写过了。