Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization

这是我参与11月更文挑战的第3天，活动详情查看：2021最后一次更文挑战。

ICCV 2017

Gatys方法适应多种风格，但太慢；前馈神经网络快，但风格固定。作者提出一种适应任何风格的实时转换方法，核心为ALADIN层（自适应内容归一化），速度接近前馈方法。

VAE（自动变分编码器），auto_regression model（自回归模型)，GAN（生成对抗网络），其中GAN的效果最好

BN通过归一化特征图统计量简化训练，一开始是被用来加速判别器的训练，但也被发现在生成图像建模中有用。其统计特征是基于一整个Batch。

BN(x) = \gamma(\frac{x - \mu(x)}{\sigma(x)}) + \beta

其中 $\gamma$ 和 $\beta$ 是从数据中学习的仿射参数， $\mu(x)$ 和 $\sigma(x)$ 每个channel独立计算，N为Batchsize大小，具体公式如下：

\mu_c(x) = \frac{1}{NHW}\sum^N_{n=1}\sum^H_{h=1}\sum^W_{w=1}x_{nchw}

\sigma_c(x) = \sqrt{\frac{1}{NHW}\sum^N_{n=1}\sum^H_{h=1}\sum^W_{w=1}(x_{nchw} - \mu_c(x))^2+\epsilon}

IN是针对BN在风格转化中的改进，针对每个通道和每个样本独立计算：

\mu_{nc}(x) = \frac{1}{HW}\sum^H_{h=1}\sum^W_{w=1}x_{nchw}

\sigma_{nc}(x) = \sqrt{\frac{1}{HW}\sum^H_{h=1}\sum^W_{w=1}(x_{nchw} - \mu_{nc}(x))^2+\epsilon}

改进了仿射变换参数 $\mu(x)$ 和 $\sigma(x)$ ，不是只学习两个参数，而是两组。用不同的参数组合即可控制生成不同的风格。但它的缺点在于额外的参数量和style个数呈线性关系，所以不适用于对需要大量风格的任务建模。

x为内容输入，y为样式输入，两者通过以下公式自适应耦合。

AdaIN(x,y) = \sigma(y)(\frac{x - \mu(x)}{\sigma(x)}) + \mu(y)

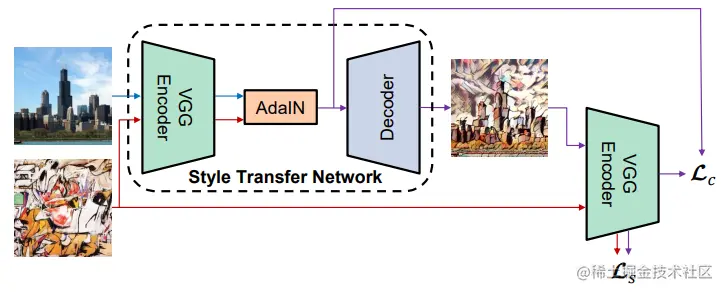
Encoder使用预训练过的VGG的前几层，编码后将内容和风格的特征图送入AdaIN产生目标特征图。decoder被随机初始化，在训练中学习将目标特征图映射回图像空间。

Loss函数是 $L_{style}$ 和 $L_{content}$ 的线性加权和， $L_{content}$ 依然是欧式距离，但 $L_{content}$ 不再是Gatys使用的Gram Matrix，作者选择计算原始风格图和生成图在encoder中逐层的均值和方差差异：

L_s = \sum^L_{i = 1}\Vert{\mu(\phi_i(g(t)))-\mu(\phi_i(s))}\Vert_2 + \sum^L_{i = 1}\Vert{\sigma(\phi_i(g(t)))-\sigma(\phi_i(s))}\Vert_2