0/前言

偏差：bias        真实值与期望值之间的diff
方差：variance    形容数据的分散程度
误差：error       偏差+方差

衡量一个模型的优劣，我们不能仅仅考虑偏差或者方差，
而是应该多方面的去衡量该模型的优劣。
偏差bias：衡量的是真实值与预测值之间的diff
方差：衡量的是该模型的稳定性。及输出是否稳定。

1/偏差bias

首先三者之间的联系是 Error = Bias + Variance。
Error反映的是整个模型的准确度，
一般来讲，我们所说的模型的好坏(优劣)，指的就是准确率error。
然后细分的话，这其中还包括偏差和方差。

说白了就是你给出的模型，你input一个值，模型输出的值和实际的值的吻合程度，吻合度高就是Error低。

Bias反映的是模型在样本上的输出与真实值之间的diff，即模型本身的精准度，
其实Bias在股票上也有应用，也可以反映股价在波动过程中与移动平均线偏离程度。

我们知道Bias是受算法模型的复杂度决定的，
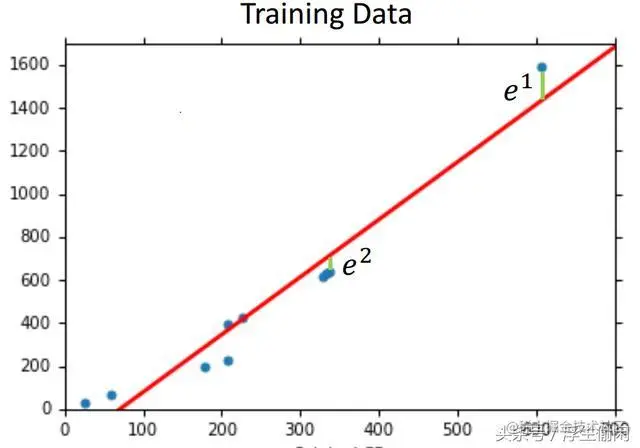
假设下图的红线是我们训练出来的模型，蓝色的点就是真实的样本点，这是一个最简单的线性模型。
这个时候Bias就可以通过这些蓝色的点到红线沿Y轴的垂直距离来反映（即真实值与模型输出的diff），
距离越大说明Bias越大，也说明拟合度更低，拟合的不够充分，也就是欠拟合。

当我们增加模型的复杂度，上图是一个线性的模型，下图是一个4次方的模型。

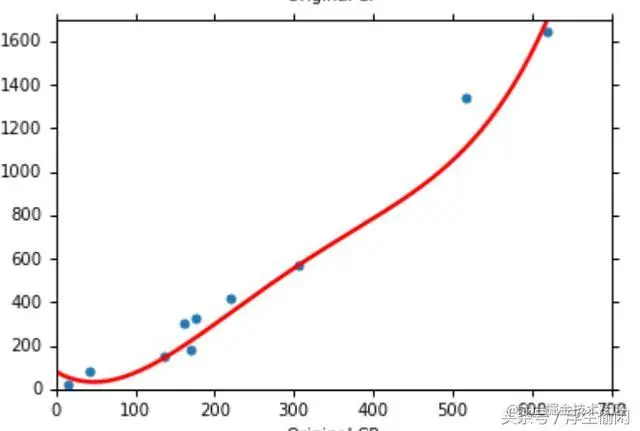
可以明显看出点到模型的沿Y轴的垂直距离更少了，即拟合度更高了，所以Bias也更低了。
所以这样我们就可以很容易理解Bias的大小和模型复杂度之间的关系了。

给出结论：当模型复杂度上升时，Bias减小。当模型复杂度降低时，Bias增加。
当模型过于复杂或者过于不复杂，这里就涉及到了欠拟合和过拟合的问题了。

2/方差variance

Variance反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性。
在概率论和统计学中方差是衡量随机变量或一组数据时离散程度的度量。

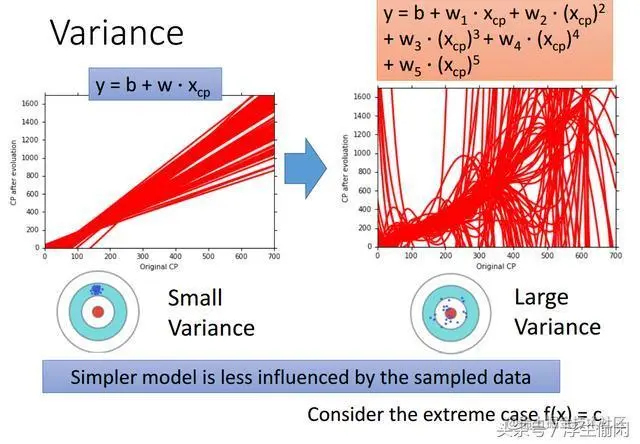
下图中红线就是每一组样本对应的模型，
想象一下真实数据有无限多，我们以10个样本为一组，选取了500个样本组，
然后在线性模型下，针对这500个样本组，我们会有500组不同的b和w值组成的线性模型，最后构成左图的样子。

当我们的模型升级成5次方的复杂程度时，针对这500个样本组(500条线)，我们会有右边这张图显示的500组不同的参数构成的模型。
可以看出，明显右边的图比左边的图更离散一些，试想一个极端情况，当模型就是一个常数时，这个时候模型复杂度最低，同时Variance也为0。
所以我们可以得出结论：当模型复杂度低时，Variance更低，当模型复杂度高时，Variance更高。

3/误差error

 error = bias + variance
 

4/一个形象的例子

想象你开着一架黑鹰直升机，得到上级命令攻击地面上一只敌军部队，
于是你连打数十梭子子弹，结果有一下几种情况:

1.子弹基本上都打在队伍旁边的一棵树上了，连在那棵树旁边等兔子的人都毫发无损，
   这就是方差小（子弹打得很集中），偏差大（跟目的相距甚远）。
   
2.子弹打在了树上，石头上，树旁边等兔子的人身上，花花草草也都中弹，但是敌军安然无恙，
   这就是方差大（子弹到处都是，不集中），偏差也大（同1）。
   
3.子弹打死了一部分敌军，但是也打偏了些打到花花草草了，
  这就是方差大（子弹不集中），偏差小（已经在目标周围 了）。
  
4.子弹一颗没浪费，每一颗都打死一个敌军，
  这就是方差小（子弹全部都集中在一个位置），偏差小（子弹集中的位置正是期望子弹该射向的位置）。

方差：是形容数据分散程度的，算是“无监督的”，客观的指标，
偏差：形容数据跟我们期望的中心差得有多远，算是“有监督的”，有人的知识参与的指标。

5/总结

一、Bias和模型复杂度的关系：当模型复杂度上升时，Bias减小。
   当模型复杂度降低时，Bias增加。（反比关系）
   当模型的复杂度多大，就容易导致过拟合了。

二、Variance和模型复杂度的关系：当模型复杂度低时，Variance更低，
   当模型复杂度高时，Variance更高。（正比关系）

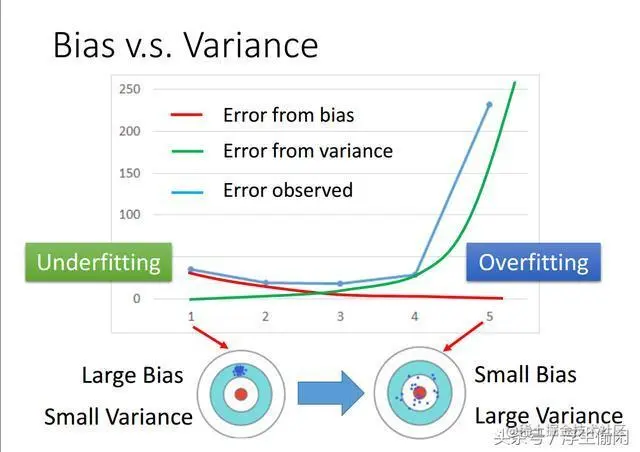
一开始我们就知道Error = Bias + Variance。
整个模型的准确度和这两个都有关系，所以这下看似是有些矛盾的。
如何才能取到最小的Error呢，看下图，蓝线就是Error的伴随Bias和Variance的变化情况，可以看出横坐标3应该是一个较好的结果。所以我们需要找到一个平衡点取得最优解。