神经网络正向传播

2021-11-05 1,202 阅读1分钟

神经网络正向传播

单层神经网络

结构图

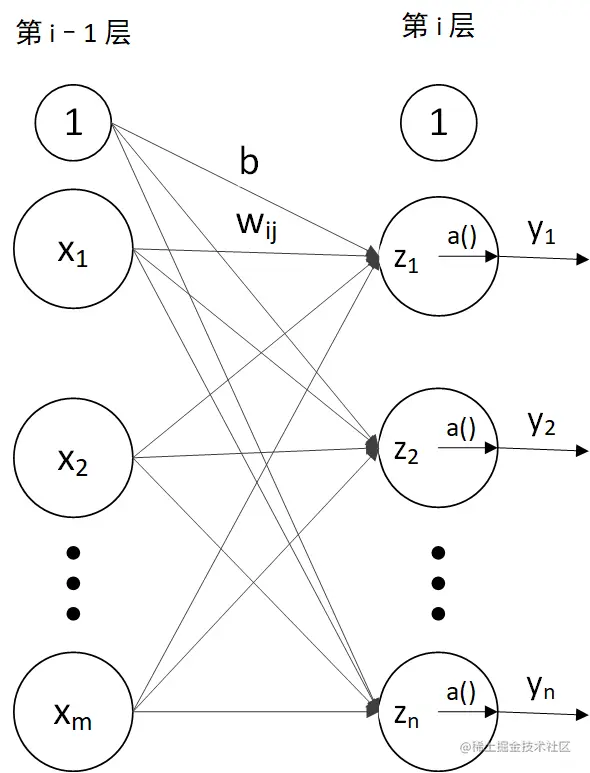
神经网络1.png

公式

\begin{bmatrix}z_1 \\z_2 \\\vdots \\z_n \\ \end{bmatrix} = \begin{bmatrix}w^{(i)}_{11} & w^{(i)}_{12} & \cdots & w^{(i)}_{1m} \\w^{(i)}_{21} & w^{(i)}_{22} & \cdots & w^{(i)}_{2m} \\\vdots & \vdots & & \vdots \\w^{(i)}_{n1} & w^{(i)}_{n2} & \cdots & w^{(i)}_{nm} \\ \end{bmatrix} \begin{bmatrix}x_1 \\x_2 \\\vdots \\x_n \\ \end{bmatrix} + \begin{bmatrix}b^{(i)}_1 \\b^{(i)}_2 \\\vdots \\b^{(i)}_n \\ \end{bmatrix}

z^{(i)} = W^{(i)}\cdot x + b^{(i)}

\begin{bmatrix}y_1 \\y_2 \\\vdots \\y_n \\ \end{bmatrix} = a\begin{pmatrix}\begin{bmatrix}z_1 \\z_2 \\\vdots \\z_n \\ \end{bmatrix}\end{pmatrix}

y^{(i)} = a(z^{(i)})

术语

偏置 $b$

控制神经元被激活的容易程度

权重 $w^l_{ij}$

$l$ 指第 $l$ 层
$i$ 指第 $l$ 层的第 $i$ 个神经元
$j$ 指第 $l - 1$ 层的第 $j$ 个神经元

$z^{(i)}$

第 $i$ 层的中间结果

$y^{(i)}$

第 $i$ 层的输出

三层神经网络

结构图

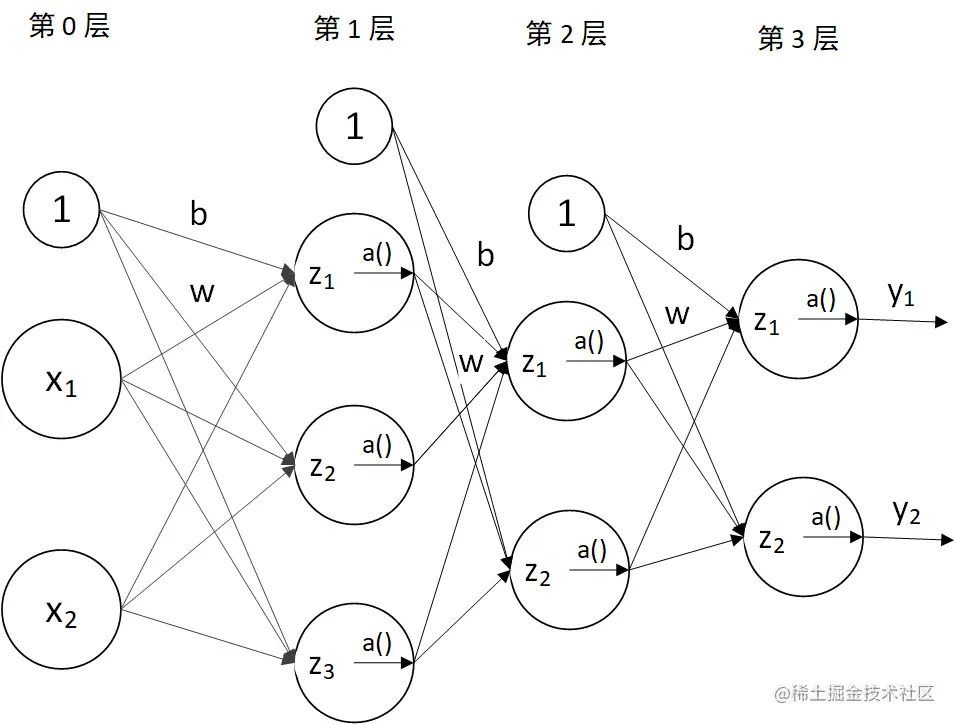
神经网络2.png

术语

one-hot

正解为 1, 其余为 0

normalize

正规化, 标准化, 归一化

将数据弄到 $0\sim1$ 之间

批处理

一次处理一批数据, 矩阵计算

batch 批
batch 批数据大小

激活函数

sigmoid

f(x) = \frac{1}{1+e^{-x}}

阶跃函数

f(x) = \begin{cases} 1 & x > 0 \\ 0 & x \leq 0 \end{cases}

relu

f(x) = \begin{cases} x & x > 0 \\ 0 & x \leq 0 \end{cases}

输出层的激活函数

恒等函数(回归)

f(x) = x

softmax(分类)

f(x) = \frac{e^{x_i}}{e^{x_1} + \cdots + e^{x_n}}

处理数据溢出, 防止 $e^{x_i}$ 很大

\begin{aligned} f(x) = \frac{e^{x_i - c}}{e^{x_1 - c} + \cdots + e^{x_n - c}} & & c = max\{x_1 ,\cdots, x_n\} \end{aligned}