分而治之

• 分而治之是算法设计中的一种方法
• 它将一个问题分成多个和原问题相似的小问题，递归解决小问题，再将结果合并以解决原来的问题

使用场景

场景一 ：归并排序

• 分： 把数组从中间一分为二
• 解： 递归的对两个子数组进行归并排序
• 合： 合并有序子数组

场景二 ： 快速排序

• 分： 选基准，按基准把数组分成两个子数组
• 解： 递归的对两个子数组进行快速排序
• 合： 对两个子数组进行合并

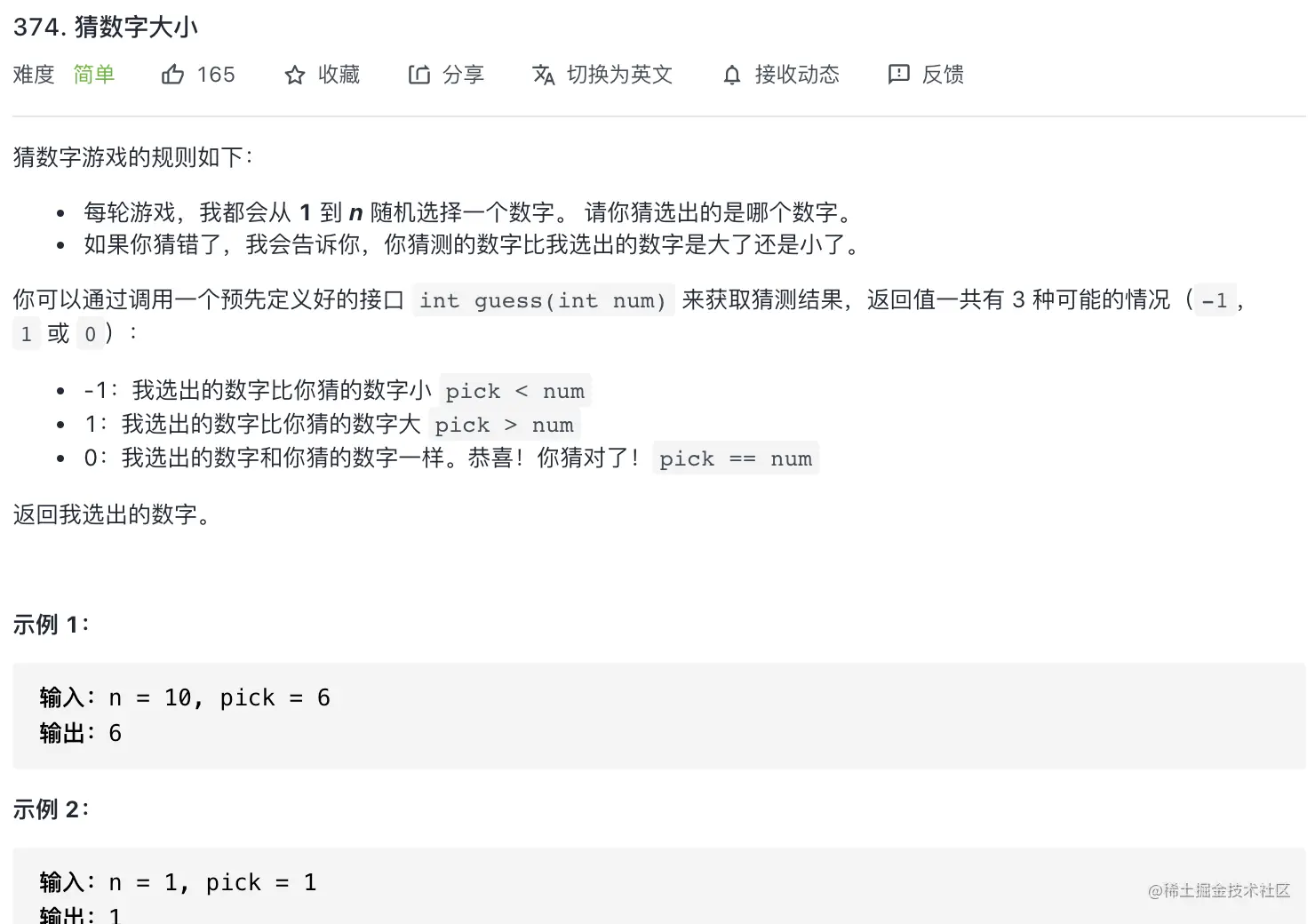
leetcode-cn.com 算法题实战

完整题目请打开 leetcode

374. 猜数字大小

解题思路

• 二分搜索，同样具备“分 解 合”的特性
• 考虑选择分而治之
• 分： 计算中间元素，分割数组
• 解： 递归的在较大或者较小数组进行二分搜索
• 合： 不需要此步，因为在子数组中搜到就返回了

/** 
 * Forward declaration of guess API.
 * @param {number} num   your guess
 * @return 	            -1 if num is lower than the guess number
 *			             1 if num is higher than the guess number
 *                       otherwise return 0
 * var guess = function(num) {}
 */

/**
 * @param {number} n
 * @return {number}
 */
var guessNumber = function(n) {
    const rec= (low,high) => {

        const mid = Math.floor((low + high)/2);
        const result = guess(mid);
        if(result === -1) {
            return rec(low,mid -1 )
        } else if(result === 1) {
             return rec(mid + 1, high)
        } else {
            return mid;
        }
    }

    return rec(1,n)
};

226. 翻转二叉树

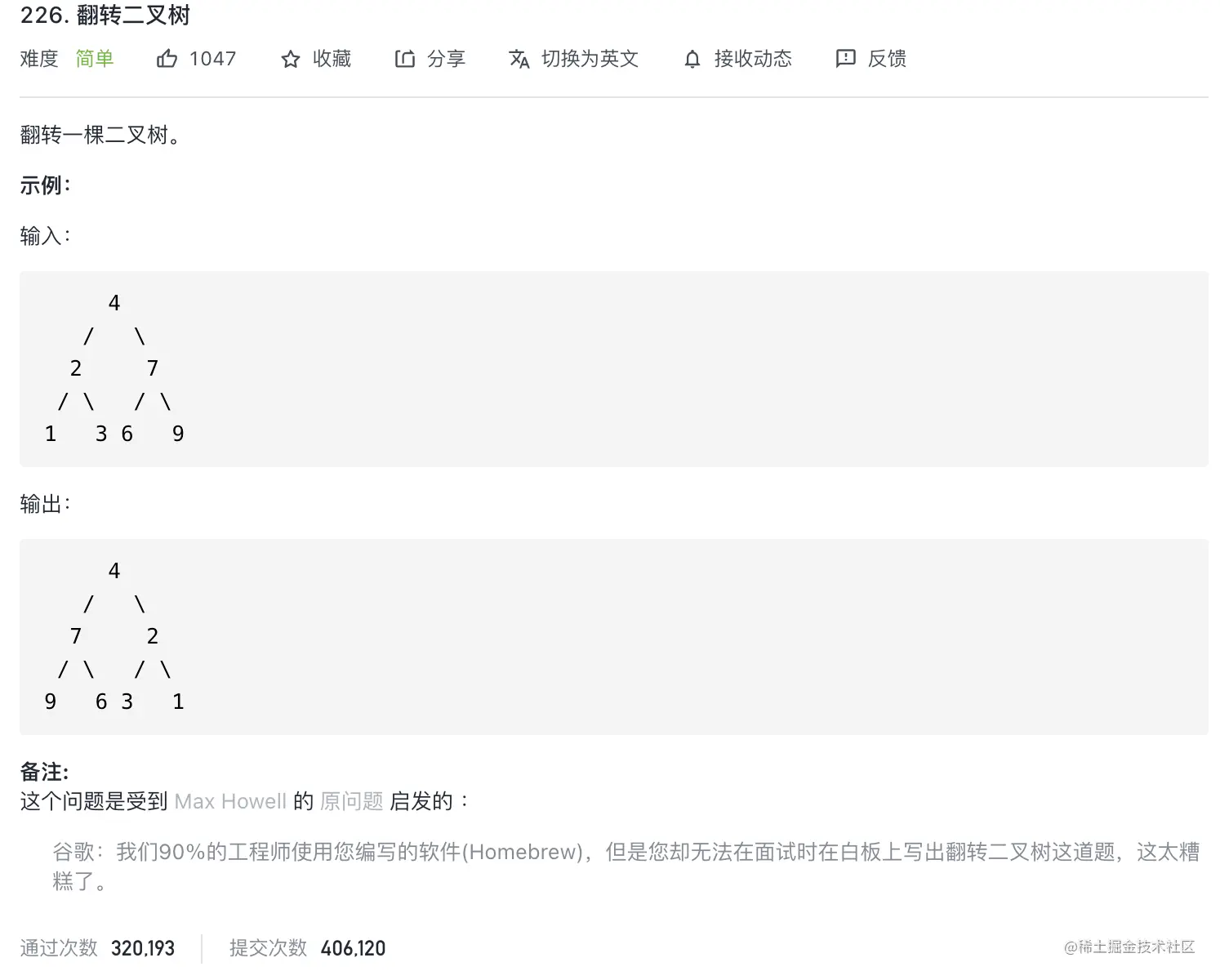
解题思路

• 先翻转左右子树，在将子树换个位置
• 符合“分 解 合” 特性
• 考虑选择分而治之
• 获取左右子树
• 解： 递归的翻转左右子树
• 合： 将翻转后的左右子树换个位置放到根节点上

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function(root) {
   
    if(!root) {return null}
    return {
        val: root.val,
        left : invertTree(root.right),
        right: invertTree(root.left)
    }
};

100. 相同的树

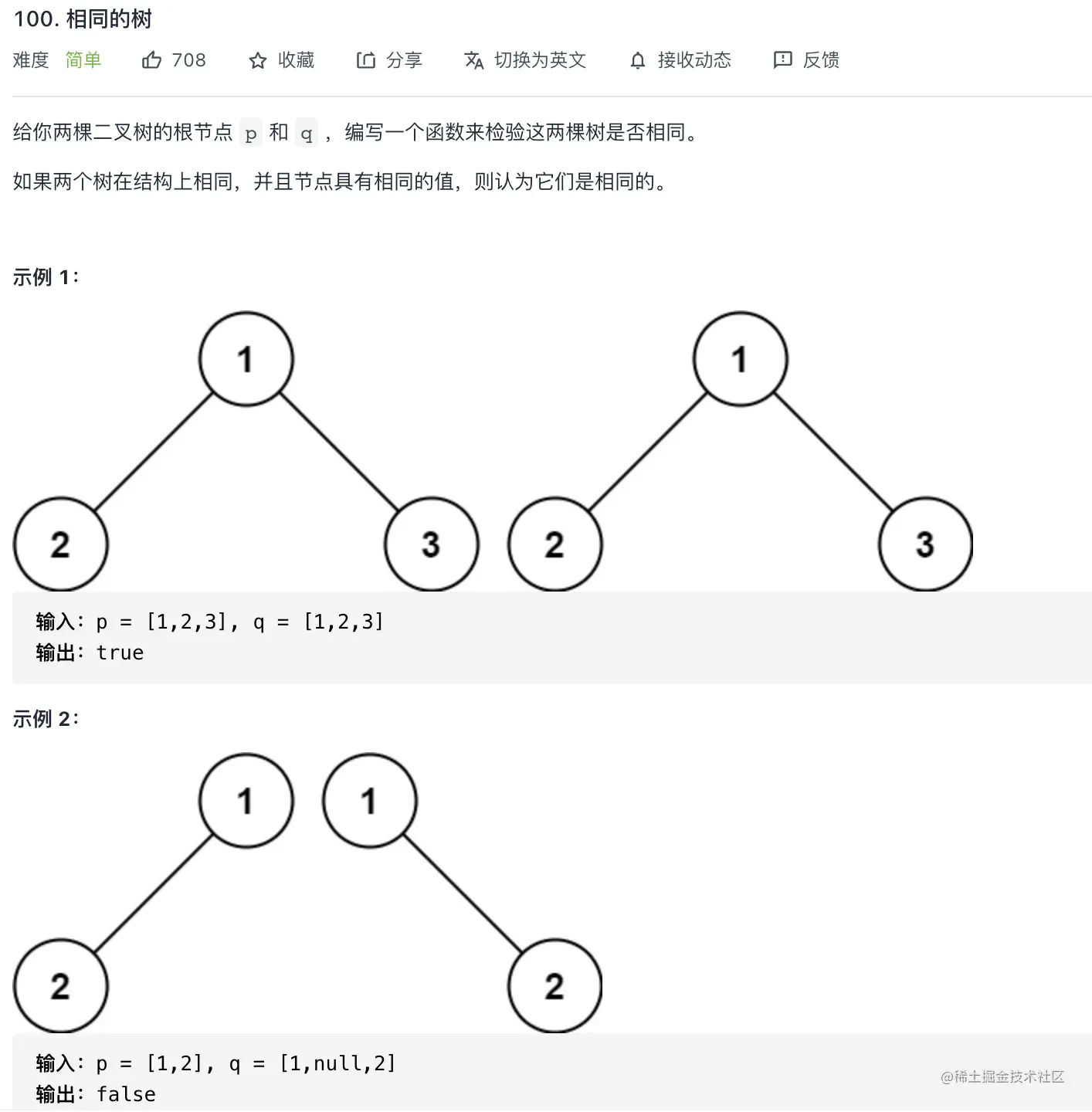
解题思路

• 两个数： 根节点的值相同，左子树相同，右子树相同
• 符合“分 解 合” 特性
• 考虑分而治之
• 分： 获取两个树的左子树和右子树
• 解： 递归的判断两个树的左子树是否相同，右子树是否相同
• 合： 将上述结果合并，如果根节点也相同，树就相同

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function(p, q) {
    if(!p && !q) { return true}
    if(p && q && p.val === q.val 
    && isSameTree(p.left,q.left) 
    && isSameTree(p.right,q.right)) {
        return true;      
    }
    return false;
};

101. 对称二叉树

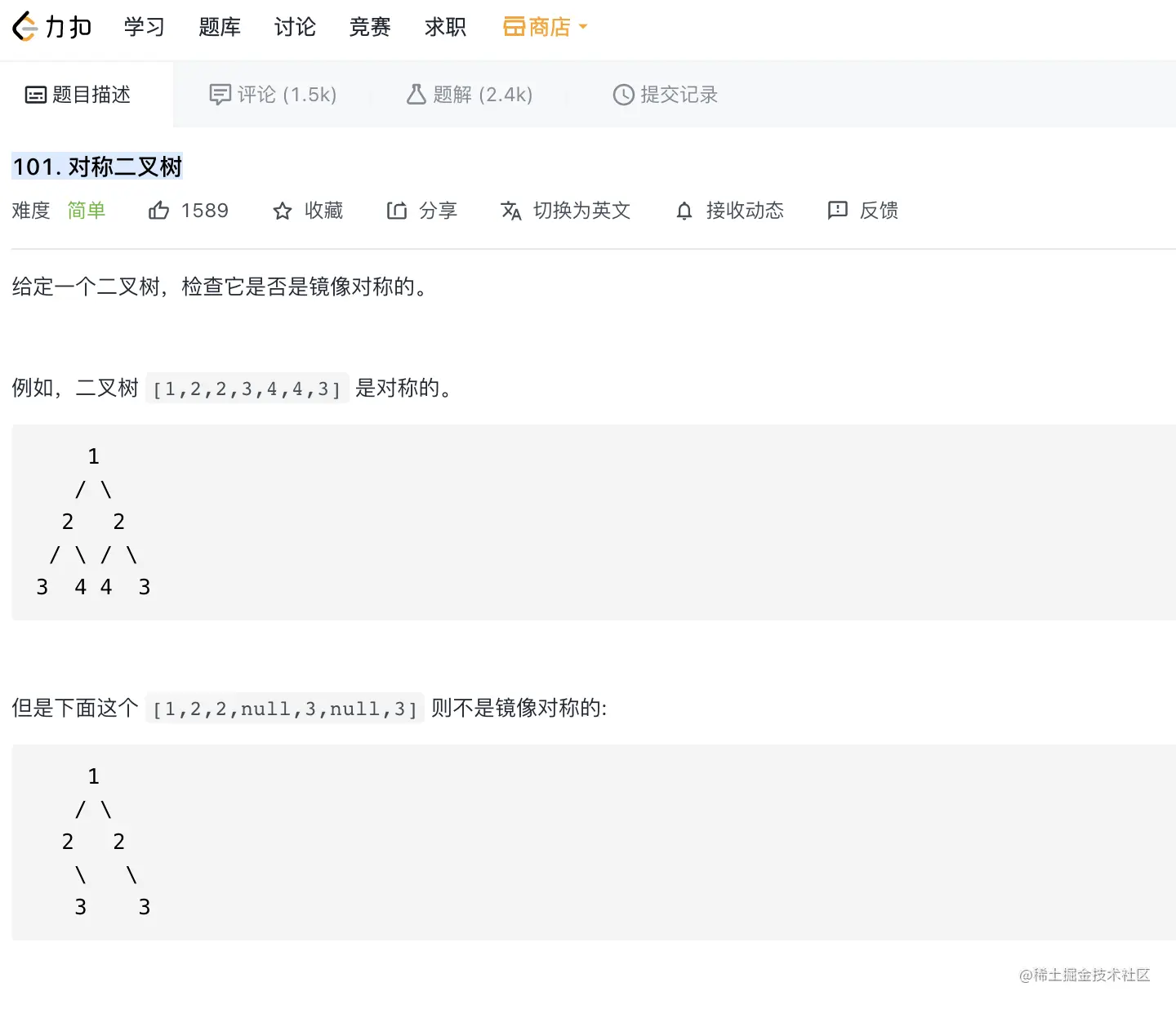
解题思路

• 转化为： 左右子树是否是镜像
• 分解为： 树1的左子树合树2的右子树是否是镜像的，树1的右子树合树2的左子树是否是镜像的
• 符合“分 解 合”特性，考虑选择分而治之
• 分： 获取两个树的左子树合右子树
• 解：递归的判断树1 的左子树合树2的右子树是否是镜像，树1的右子树合树2左子树是否是镜像
• 合： 如果上述都成立，且根节点值也相同，两个树就是镜像

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isSymmetric = function(root) {
    if(!root) {return true}
    const isMirror = (l,r) => {
        if(!l && !r) return true;
        if(l && r &&l.val === r.val && isMirror(l.left,r.right) && isMirror(l.right,r.left)) {
            return true;
        }
        return false;
    }
    return isMirror(root.left,root.right)
};

下一站 动态规划