详解惯性导航论文 RINS-W: Robust Inertial Navigation System on Wheels

10点43
1,486 阅读5分钟

image.png 本文介绍一篇惯性导航定位论文 RINS-W，论文发表于 IROS2019。在本论文中作者提出了仅使用一个IMU进行长时间惯性导航的方法。方法主要包括两个部分：

  • 检测器使用循环神经网络来检测IMU的运动状况，如零速或零横向滑移；
  • 使用Invariant Extended Kalman Filter结合检测器的输出（作为伪测量）来进行定位。

在公开数据集上的测试结果显示，在行驶超过21km之后，最终定位误差为20m（如下图所示）。

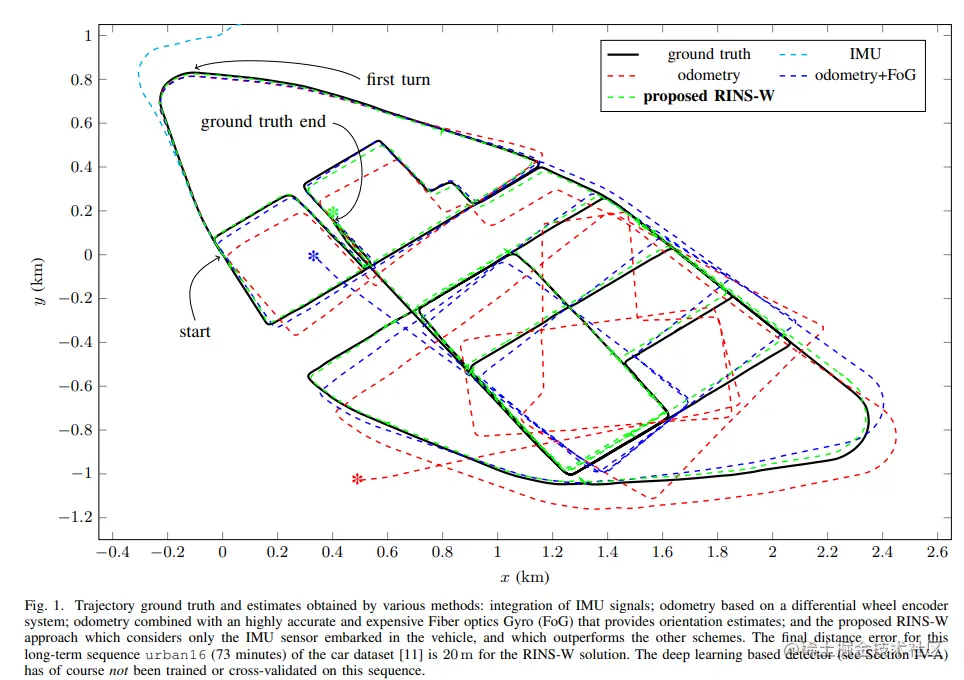
image.png

论文链接：arxiv.org/pdf/1903.02…

1. Inertial Navigation System & Sensor Model

首先回顾下惯性导航方程，IMU方向用 Rn∈SO(3)\mathbf{R}_n \in SO(3) 表示，表示从载体坐标到世界坐标的旋转变换；世界坐标系中速度为 vnw∈R3\mathbf{v}_{n}^{\mathrm{w}} \in \mathbb{R}^{3}，世界坐标系中位置为 pnw∈R3\mathbf{p}_{n}^{\mathrm{w}} \in \mathbb{R}^{3}，则运动方程可以写为：

Rn+1=Rnexp⁡SO(3)(ωndt)vn+1w=vnW+(Rnan+g)dtpn+1w=pnw+vnwdt\begin{aligned} \mathbf{R}_{n+1} &=\mathbf{R}_{n} \exp _{S O(3)}\left(\boldsymbol{\omega}_{n} d t\right) \\ \mathbf{v}_{n+1}^{\mathrm{w}} &=\mathbf{v}_{n}^{\mathrm{W}}+\left(\mathbf{R}_{n} \mathbf{a}_{n}+\mathbf{g}\right) d t \\ \mathbf{p}_{n+1}^{\mathrm{w}} &=\mathbf{p}_{n}^{\mathrm{w}}+\mathbf{v}_{n}^{\mathrm{w}} d t \end{aligned}

其中 dtdt 时采样时间，(R0,v0w,p0w)(\mathbf{R}_0,\mathbf{v}_{0}^{\mathrm{w}},\mathbf{p}_{0}^{\mathrm{w}}) 是初始状态。在本论文中，没有考虑地球自转和科氏力的影响。

下面回顾下IMU模型，IMU加速度和角速度模型可以写为：

ωnIMU=ωn+bnω+wnωanIMU=an+bna+wna\begin{aligned} &\boldsymbol{\omega}_{n}^{\mathrm{IMU}}=\boldsymbol{\omega}_{n}+\mathbf{b}_{n}^{\boldsymbol{\omega}}+\mathbf{w}_{n}^{\boldsymbol{\omega}} \\ &\mathbf{a}_{n}^{\mathrm{IMU}}=\mathbf{a}_{n}+\mathbf{b}_{n}^{\mathbf{a}}+\mathbf{w}_{n}^{\mathbf{a}} \end{aligned}

其中，bnω,bna\mathbf{b}_{n}^{\boldsymbol{\omega}},\mathbf{b}_{n}^{\mathbf{a}}为角速度偏差和加速度偏差，wnω，wna\mathbf{w}_{n}^{\boldsymbol{\omega}}，\mathbf{w}_{n}^{\mathbf{a}} 为高斯噪声。角速度偏差和加速度偏差方程可以写为：

bn+1ω=bnω+wnbωbn+1a=bna+wnba\begin{aligned} \mathbf{b}_{n+1}^{\boldsymbol{\omega}}=\mathbf{b}_{n}^{\boldsymbol{\omega}}+\mathbf{w}_{n}^{\mathbf{b}_{\boldsymbol{\omega}}} \\ \mathbf{b}_{n+1}^{\mathbf{a}}=\mathbf{b}_{n}^{\mathbf{a}}+\mathbf{w}_{n}^{\mathbf{b}_{\mathbf{a}}} \end{aligned}

其中，wnbω,wnba\mathbf{w}_{n}^{\mathbf{b}_{\boldsymbol{\omega}}},\mathbf{w}_{n}^{\mathbf{b}_{\mathbf{a}}} 为随机游走噪声。

在惯性导航中，偏差的准确估计是至关重要的，即使很小的误差，也会导致很大的位置估计偏差。

2. Specific Motion Profiles For Wheeled Systemd

在这一节，作者介绍了几种常见的运动特性，它们往往会提供有用的互补信息。

首先是四种特定的运动情况，将它们编码为向量形式为：

zn=(znVEL,znANG,znLAT,znUP)∈{0,1}4\mathbf{z}_{n}=\left(z_{n}^{\mathrm{VEL}}, z_{n}^{\mathrm{ANG}}, z_{n}^{\mathrm{LAT}}, \quad z_{n}^{\mathrm{UP}}\right) \in\{0,1\}^{4}

其中：

  • Zero velocity，当 znVEL=1z_n^{\mathrm{VEL}}=1 时，则有{vn=0Rnan+g=0\left\{\begin{array}{c}\mathbf{v}_{n}=\mathbf{0} \\ \mathbf{R}_{n} \mathbf{a}_{n}+\mathbf{g}=\mathbf{0}\end{array}\right.，当检测到零速时，常会使用 ZUPT 算法进行更新。
  • Zero angular velocity，当 znANG=1z_n^{\mathrm{ANG}}=1 时，则有 ωn=0\boldsymbol{\omega}_{n}=\mathbf{0}。
  • Zero lateral velocity，当 znLAT=1z_n^{\mathrm{LAT}}=1 时，则有 vnLAT≃0v_{n}^{\mathrm{LAT}} \simeq 0，载体坐标速度和世界坐标速度转换方程为：vnB=RnTvnW=[vnFORvnLATvnUP]\mathbf{v}_{n}^{\mathrm{B}}=\mathbf{R}_{n}^{T} \mathbf{v}_{n}^{\mathrm{W}}=\left[\begin{array}{c}v_{n}^{\mathrm{FOR}} \\ v_{n}^{\mathrm{LAT}} \\ v_{n}^{\mathrm{UP}}\end{array}\right]。
  • Zero vertical velocity，当 znUP=1z_n^{\mathrm{UP}}=1 时，则有 vnUP≃0v_{n}^{\mathrm{UP}} \simeq 0。

其中，后两种运动情况经常用在轮速机器人或汽车运动中。以上四种情形中，零速约束（零速度和零角速度）用来修正IMU偏差和姿态俯仰角；零横向速度和垂直速度用来长期估计汽车位置（后面的实验会进行说明）。

3. Proposed RINS-W Algorithm

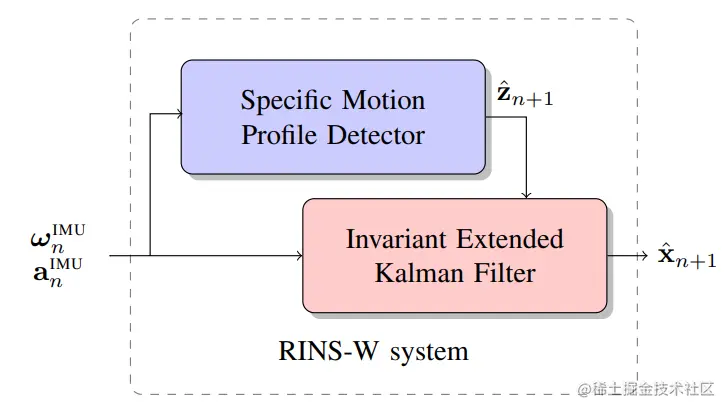
本文提出的方法如下图所示，由两部分组成：

  • Detector 由循环神经网络组成，根据IMU测量值来输出二元向量 zn\mathbf{z}_n；
  • IEKF 是一种新的卡尔曼滤波器，输入为IMU测量值和检测器输出（作为伪测量），对状态量进行估计；

image.png

3.1 Specific Motion Profile Detector

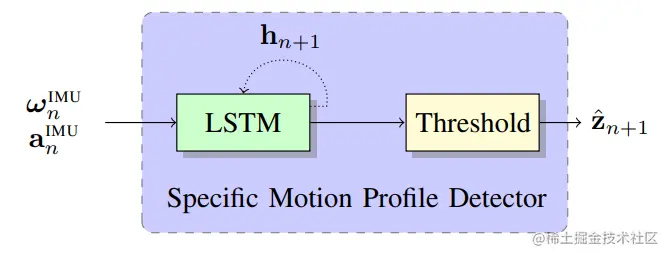
Detector 会决定在每一个时刻 nn 二元向量 zn\mathbf{z}_n中有几个元素是有效的，即有几种运动形式会发生，结构如下图所示。检测器的核心模块为LSTM，输入为IMU测量值，计算方程为：

u^n+1,hn+1=LSTM⁡({ωiIMU,aiIMU}i=0n)=LSTM⁡(ωnIMU,anIMU,hn)\begin{aligned} \hat{\mathbf{u}}_{n+1}, \mathbf{h}_{n+1} &=\operatorname{LSTM}\left(\left\{\boldsymbol{\omega}_{i}^{\mathrm{IMU}}, \mathbf{a}_{i}^{\mathrm{IMU}}\right\}_{i=0}^{n}\right) \\ &=\operatorname{LSTM}\left(\boldsymbol{\omega}_{n}^{\mathrm{IMU}}, \mathbf{a}_{n}^{\mathrm{IMU}}, \mathbf{h}_{n}\right) \end{aligned}

其中，u^n+1∈R4\hat{\mathbf{u}}_{n+1} \in \mathbb{R^4} 包含每一个运动情形的概率值，hn\mathbf{h}_n 是神经网络隐藏状态，概率值最后经过阈值运算来得到二元向量 z^n=Threshold(u^n+1)\hat{\mathbf{z}}_n=\mathrm{Threshold} \left(\hat{\mathbf{u}}_{n+1}\right)

image.png

3.2 The Invariant Extended Kalman Filter（重点）

在本文中，作者选择使用IEKF而不是传统的EKF来作为进行状态估计，如下图所示，二元变量 z^n\hat{\mathbf{z}}_n 一方面会用于状态传播，另一方面会用于状态更新。

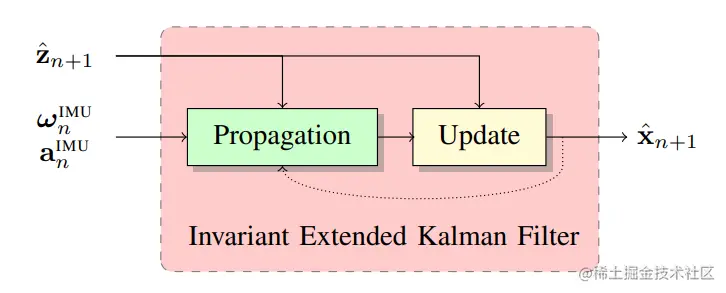
image.png

（1）首先定义IMU状态，IMU状态量为：xn=(Rn,vnw,pnw,bnω,bna)\mathbf{x}_{n}=\left(\mathbf{R}_{n}, \mathbf{v}_{n}^{\mathrm{w}}, \mathbf{p}_{n}^{\mathrm{w}}, \mathbf{b}_{n}^{\boldsymbol{\omega}}, \mathbf{b}_{n}^{\mathbf{a}}\right)，线性状态误差为：en=[ξnenb]∼N(0,Pn)\mathbf{e}_{n}=\left[\begin{array}{c}\boldsymbol{\xi}_{n} \\ \mathbf{e}_{n}^{\mathbf{b}}\end{array}\right] \sim \mathcal{N}\left(\mathbf{0}, \mathbf{P}_{n}\right)，状态更新方程为：

χn=exp⁡SE2(3)(ξn)χ^nbn=b^n+enb,\begin{aligned} &\boldsymbol{\chi}_{n}=\exp _{S E_{2}(3)}\left(\boldsymbol{\xi}_{n}\right) \hat{\boldsymbol{\chi}}_{n} \\ &\mathbf{b}_{n}=\hat{\mathbf{b}}_{n}+\mathbf{e}_{n}^{\mathbf{b}}, \end{aligned}

其中，χn∈SE2(3)\boldsymbol{\chi}_{n} \in SE_2(3)，表示为汽车状态 (Rn,vnw,pnw)(\mathbf{R}_{n}, \mathbf{v}_{n}^{\mathrm{w}}, \mathbf{p}_{n}^{\mathrm{w}}) 在李群上的形式，误差状态协方差矩阵为 Pn∈R15×15\mathbf{P}_{n} \in \mathbb{R}^{15 \times 15}。偏差 bn=(bnω,bna)∈R6\mathbf{b}_n=({ \mathbf{b}_{n}^{\boldsymbol{\omega}}, \mathbf{b}_{n}^{\mathbf{a}})} \in \mathbb{R}^6，偏差估计量为 b^n=(b^nω,b^na)∈R6\hat{\mathbf{b}}_{n}=\left(\hat{\mathbf{b}}_{n}^{\omega}, \hat{\mathbf{b}}_{n}^{\mathbf{a}}\right) \in \mathbb{R}^{6}。

（2）预测部分。当没有上述四种之一的运动情况被检测到时，使用第1节介绍的运动方程来计算新的状态量和协方差，协方差计算方程为：

Pn+1=FnPnFnT+GnQnGnT\mathbf{P}_{n+1}=\mathbf{F}_{n} \mathbf{P}_{n} \mathbf{F}_{n}^{T}+\mathbf{G}_{n} \mathbf{Q}_{n} \mathbf{G}_{n}^{T}

雅可比矩阵 Fn,Gn\mathbf{F}_n,\mathbf{G}_n 将会在第5节进行介绍。Qn\mathbf{Q}_n 表示为噪声协方差矩阵，噪声为 wn=(wnω,wna,wnbω,wnba)∼N(0,Qn)\mathbf{w}_{n}=\left(\mathbf{w}_{n}^{\boldsymbol{\omega}}, \mathbf{w}_{n}^{\mathbf{a}}, \mathbf{w}_{n}^{\mathbf{b} \omega}, \mathbf{w}_{n}^{\mathbf{b}^{\mathrm{a}}}\right) \sim \mathcal{N}\left(\mathbf{0}, \mathbf{Q}_{n}\right)。

如果由特定的运动情况被检测到，将会按照下面的方程进行状态量修改，零速时（速度归0，位置不变，这里的0表示速度为0，原论文中作者未明确表示）：

z^n+1vEL=1⇒{vn+1w=vnw=0pn+1w=pnw\hat{z}_{n+1}^{\mathrm{vEL}}=1 \Rightarrow\left\{\begin{array}{l} \mathbf{v}_{n+1}^{\mathrm{w}}=\mathbf{v}_{n}^{\mathrm{w}} =0 \\ \mathbf{p}_{n+1}^{\mathrm{w}}=\mathbf{p}_{n}^{\mathrm{w}} \end{array}\right.

零角速度时（姿态不变）：

z^n+1ANG=1⇒Rn+1=Rn\hat{z}_{n+1}^{\mathrm{ANG}}=1 \Rightarrow \mathbf{R}_{n+1}=\mathbf{R}_{n}

同时，状态估计量和协方差矩阵也要响应进行修改。

（3）更新。每一个运动情形将会产生下列的伪测量：

yn+1VEL=[Rn+1Tvn+1Wbn+1a−Rn+1Tg]=[0anIMU]yn+1ANG=bn+1ω=ωnIMUyn+1LAT=vn+1LAT=0yn+1UP=vn+1UP=0\begin{aligned} &\mathbf{y}_{n+1}^{\mathrm{VEL}}=\left[\begin{array}{c} \mathbf{R}_{n+1}^{T} \mathbf{v}_{n+1}^{\mathrm{W}} \\ \mathbf{b}_{n+1}^{\mathbf{a}}-\mathbf{R}_{n+1}^{T} \mathbf{g} \end{array}\right]=\left[\begin{array}{c} \mathbf{0} \\ \mathbf{a}_{n}^{\mathrm{IMU}} \end{array}\right] \\ &\mathbf{y}_{n+1}^{\mathrm{ANG}}=\mathbf{b}_{n+1}^{\boldsymbol{\omega}}=\boldsymbol{\omega}_{n}^{\mathrm{IMU}} \\ &\mathbf{y}_{n+1}^{\mathrm{LAT}}=v_{n+1}^{\mathrm{LAT}}=0 \\ &\mathbf{y}_{n+1}^{\mathrm{UP}}=v_{n+1}^{\mathrm{UP}}=0 \end{aligned}

更新方程为：

K=Pn+1Hn+1T/(Hn+1Pn+1Hn+1T+Nn+1)e+=K(yn+1−y^n+1)=[ξ+eb+]χ^n+1+=exp⁡(ξ+)χ^n+1,bn+1+=bn+1+eb+Pn+1+=(I−KHn+1)Pn+1\begin{aligned} \mathbf{K} &=\mathbf{P}_{n+1} \mathbf{H}_{n+1}^{T} /\left(\mathbf{H}_{n+1} \mathbf{P}_{n+1} \mathbf{H}_{n+1}^{T}+\mathbf{N}_{n+1}\right) \\ \mathbf{e}^{+} &=\mathbf{K}\left(\mathbf{y}_{n+1}-\hat{\mathbf{y}}_{n+1}\right)=\left[\begin{array}{c} \boldsymbol{\xi}^{+} \\ \mathbf{e}^{\mathbf{b}+} \end{array}\right] \\ \hat{\boldsymbol{\chi}}_{n+1}^{+} &=\exp \left(\boldsymbol{\xi}^{+}\right) \hat{\boldsymbol{\chi}}_{n+1}, \mathbf{b}_{n+1}^{+}=\mathbf{b}_{n+1}+\mathbf{e}^{\mathbf{b}+} \\ \mathbf{P}_{n+1}^{+} &=\left(\mathbf{I}-\mathbf{K H}_{n+1}\right) \mathbf{P}_{n+1} \end{aligned}

其中，K\mathbf{K} 为卡尔曼增益矩阵，Hn+1\mathbf{H}_{n+1} 是测量雅可比矩阵（具体形式见第5节）。

（4）初始化。为了正确估计偏差和方向，在开始阶段，将会强制静止1秒钟用于估计偏差和俯仰角。

4. Results On Car Dataset

首先是数据集的介绍，使用的数据集为comples urban LiDAR Dataset，IMU如下图所示。

image.png

4.1 Implementation Details

下面是实现细节，detector由4个LSTMs组成，每一个LSTM由2个隐藏层（每层250个隐藏单元）组成，然后是2层多层感知机，最后是sigmoid函数。阈值设定为：0.95 （znVEL,znANG）（z_n^{\mathrm{VEL}},z_n^{\mathrm{ANG}}），0.5 （znLAT,znUP）（z_n^{\mathrm{LAT}},z_n^{\mathrm{UP}}）；滤波器工作频率为100Hz，噪声协方差矩阵为：

Qn=diag⁡(σω2I,σa2I,σbω2I,σba2I)Nn=diag⁡(σVEL,v2I,σVEL,a2I,σANG2I,σLAT2,σUP2)\begin{aligned} &\mathbf{Q}_{n}=\operatorname{diag}\left(\sigma_{\omega}^{2} \mathbf{I}, \sigma_{\mathbf{a}}^{2} \mathbf{I}, \sigma_{\mathbf{b}_{\boldsymbol{\omega}}}^{2} \mathbf{I}, \sigma_{\mathbf{b}_{\mathbf{a}}}^{2} \mathbf{I}\right) \\ &\mathbf{N}_{n}=\operatorname{diag}\left(\sigma_{\mathrm{VEL}, \mathbf{v}}^{2} \mathbf{I}, \sigma_{\mathrm{VEL}, \mathbf{a}}^{2} \mathbf{I}, \sigma_{\mathrm{ANG}}^{2} \mathbf{I}, \sigma_{\mathrm{LAT}}^{2}, \sigma_{\mathrm{UP}}^{2}\right) \end{aligned}

其中，协方差矩阵 QQ 中 σω=0.01rad/s,σa=0.2m/s2,σbω=0.001rad/s,σba=0.02m/s2\sigma_{\omega}=0.01 \mathrm{rad/s},\sigma_{\mathbf{a}}=0.2 \mathrm{m/s^2},\sigma_{\mathbf{b}_{\boldsymbol{\omega}}}=0.001 \mathrm{rad/s},\sigma_{\mathbf{b}_{\mathbf{a}}}=0.02\mathrm{m/s^2}；噪声矩阵 Nn\mathbf{N}_{n} 中 σVEL,v=1m/s,σVEL,a=0.4m/s2,σANG=0.04rad/s,σLAT=3m/s,σUP=3m/s\sigma_{\mathrm{VEL}, \mathbf{v}}=1\mathrm{m/s}, \sigma_{\mathrm{VEL}, \mathbf{a}}=0.4\mathrm{m/s^2}, \sigma_{\mathrm{ANG}}=0.04\mathrm{rad/s}, \sigma_{\mathrm{LAT}}=3\mathrm{m/s}, \sigma_{\mathrm{UP}}=3\mathrm{m/s}。

4.2 Evaluation Metrics

这里使用了三个评价指标：

  • Mean Absolute Trajectory Error (m-ATE)，平均绝对轨迹误差（估计位置和真值位置之间的误差平均值）；
  • Mean Absolute Aligned Trajectory Error (aligned m-ATE)，首先对齐估计轨迹和真值轨迹，然后再计算m-ATE，主要是评估轨迹的一致性；
  • Final distance error，估计轨迹和真值轨迹最终的距离误差。

4.3 Trajectory Results

下面是实验结果，作者采用了4种方法：

  • IMU直接积分方法；
  • 差分轮速编码器得到线性速度和角速度再积分；
  • RINS-W，本文提出的方法；
  • 里程计+光纤陀螺仪，里程计提供线性速度，角速度由FoG得到。
在这里插入图片描述在这里插入图片描述在这里插入图片描述

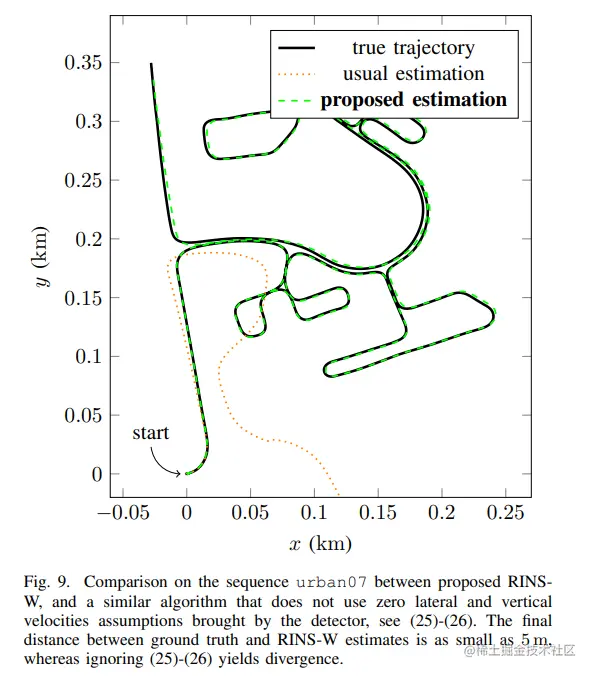
同时作者还比较了是否使用横向和垂直速度假设时的定位误差，结果如下，使用横向和垂直速度假设时效果更好。

image.png

avatar
文章
阅读
粉丝