基本概念

信息熵：表示随机变量的不确定性。

条件熵：在一个条件下，随机变量的不确定性。

信息增益：信息熵 - 条件熵。表示在一个条件下，信息不确定性减少的程度。

如何计算特征的信息增益

我们有一份数据如下：

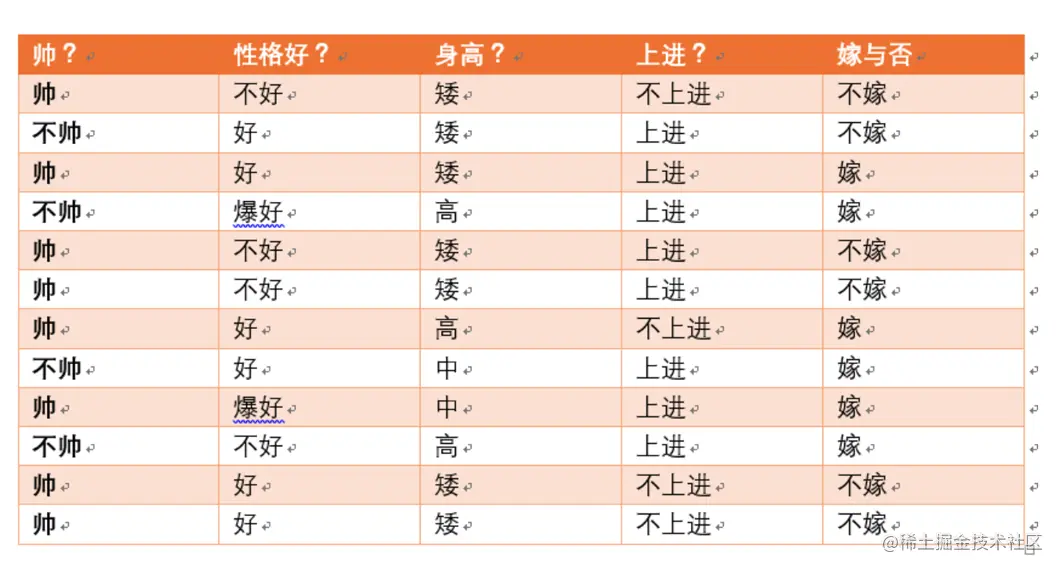
帅 性格好 身高 上进 这4个是特征
嫁与否是目标变量

可以求得该数据的信息熵是：
因为嫁的个数是6个，不嫁的个数是6个，
所以 信息熵是 -（ 6/12*log6/12 + 6/12*log6/12 ）= 0.301

假设我知道了身高信息，身高有3个特征值，矮，中，高
矮包括{1,2,3,5,6,11,12}，嫁的个数为1个，不嫁的个数为6个，共7个
中包括{8,9} ，嫁的个数为2个，不嫁的个数为0个，共2个
高包括{4,7,10}，嫁的个数为3个，不嫁的个数为0个，共3个

我们先求出公式对应的:
   H(Y|X = 矮) = -（1/7*log1/7 + 6/7*log6/7）=0.178
   H(Y|X = 中) = -（1*log1 + 0） = 0
   H(Y|X = 高） = -（1*log1 + 0）= 0
   
   p(X = 矮) = 7/12,
   p(X = 中) = 2/12,
   p(X = 高) = 3/12,

   则可以得出条件熵为：
   7/12*0.178+2/12*0+3/12*0 = 0.103
   
所以，身高这个特征的信息增益info-gain是0.301 - 0.103 = 0.198

结论

通过上述可以知道，本来如果我对一个男生什么都不知道的话，
作为他的女朋友决定是否嫁给他的不确定性有0.301这么大。

当我们知道男朋友的身高信息后，不确定度减少了0.198。
也就是说，身高这个特征对于我们广大女生同学来说，决定嫁不嫁给自己的男朋友是很重要的。
至少我们知道了身高特征后，我们原来没有底的心里（0.301）已经明朗一半多了，减少0.198了（大于原来的一半了）。

那么这就类似于非诚勿扰节目里面的桥段了，请问女嘉宾，你只能知道男生的一个特征。请问你想知道哪个特征。

假如其它特征我也全算了，身高这个特征的信息增益最大。
那么我就可以说，孟非哥哥，我想知道男嘉宾的一个特征是身高特征。
因为它在这些特征中，对于我挑夫君是最重要的，信息增益是最大的，知道了这个特征，嫁与不嫁的不确定度减少的是最多的。