哈夫曼树
树的4个概念
- 什么是路径?
在一棵树中,从一个结点到另一个结点所经过的所有结点,被我们称为两个结点之间的路径。
上面的二叉树当中,从根结点A到叶子结点H的路径,就是A,B,D,H。
- 什么是路径长度?
在一棵树中,从一个结点到另一个结点所经过的“边”的数量,被我们称为两个结点之间的路径长度。
仍然用刚才的二叉树举例子,从根结点A到叶子结点H,共经过了3条边,因此路径长度是3。
- 什么是结点的带权路径长度?
树的每一个结点,都可以拥有自己的“权重”(Weight),权重在不同的算法当中可以起到不同的作用。
结点的带权路径长度,是指树的根结点到该结点的路径长度,和该结点权重的乘积。
假设结点H的权重是3,从根结点到结点H的路径长度也是3,因此结点H的带权路径长度是 3 X 3 = 9。
- 什么是树的带权路径长度?
在一棵树中,所有叶子结点的带权路径长度之和,被称为树的带权路径长度,也被简称为WPL。
仍然以这颗二叉树为例,树的路径长度是 3X3 + 6X3 + 1X2 + 4X2 + 8X2 = 53。
哈夫曼树概念
哈夫曼树是由麻省理工学院的哈夫曼博士于1952年发明,这到底是一颗什么样的树呢?
刚才我们学习了树的带权路径长度(WPL),而哈夫曼树(Huffman Tree)是在叶子结点和权重确定的情况下,带权路径长度最小的二叉树,也被称为最优二叉树。
举个例子,给定权重分别为1,3,4,6,8的叶子结点,我们应当构建怎样的二叉树,才能保证其带权路径长度最小?
原则上,我们应该让权重小的叶子结点远离树根,权重大的叶子结点靠近树根。
下图左侧的这棵树就是一颗哈夫曼树,它的WPL是46,小于之前例子当中的53:
需要注意的是,同样叶子结点所构成的哈夫曼树可能不止一颗,下面这几棵树都是哈夫曼树:
构建一个哈夫曼树
假设有6个叶子结点,权重依次是2,3,7,9,18,25,如何构建一颗哈夫曼树,也就是带权路径长度最小的树呢?
第一步:构建森林
我们把每一个叶子结点,都当做树一颗独立的树(只有根结点的树),这样就形成了一个森林:
在上图当中,右侧是叶子结点的森林,左侧是一个辅助队列,按照权值从小到大存储了所有叶子结点。至于辅助队列的作用,我们后续将会看到。
第二步:选择当前权值最小的两个结点,生成新的父结点
借助辅助队列,我们可以找到权值最小的结点2和3,并根据这两个结点生成一个新的父结点,父节点的权值是这两个结点权值之和:
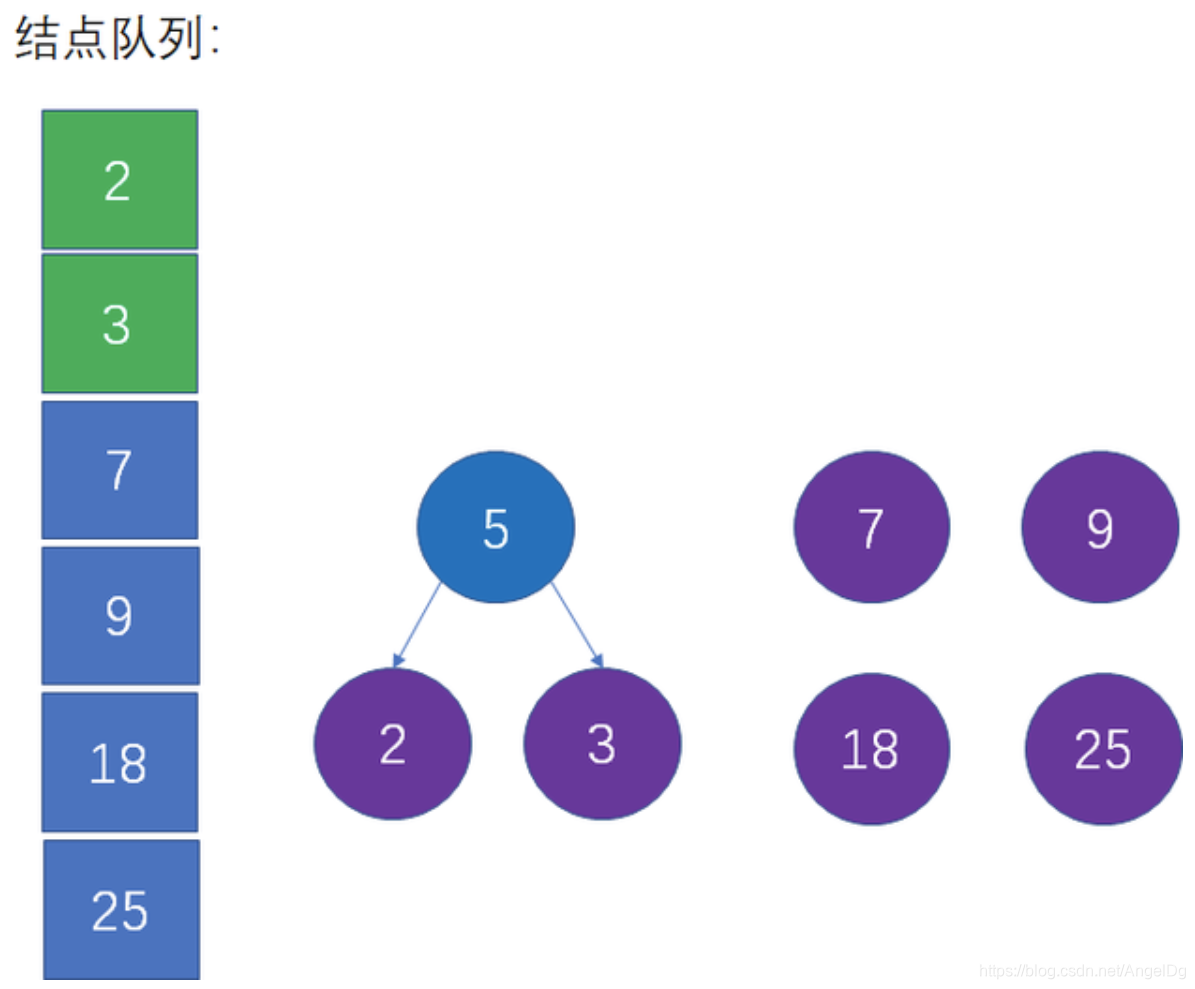
第三步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列
也就是从队列中删除2和3,插入5,并且仍然保持队列的升序:
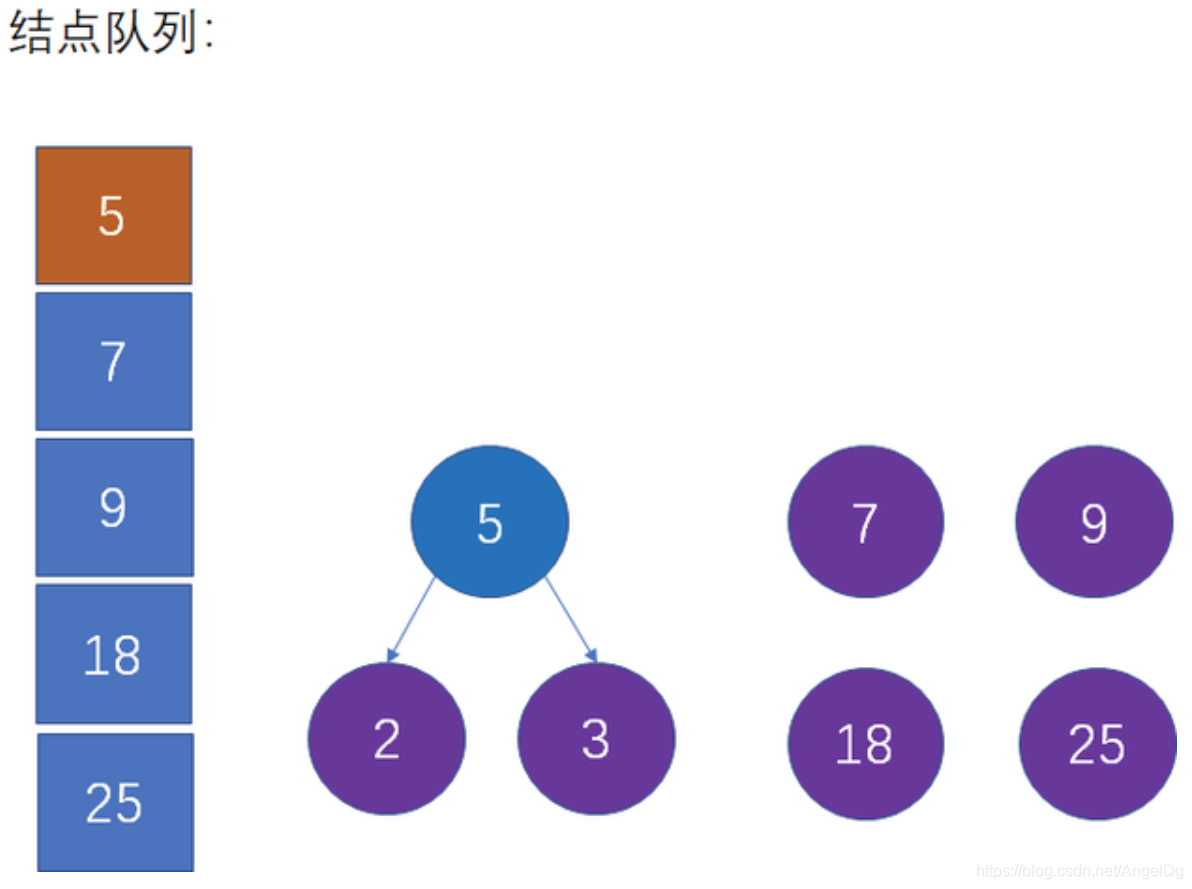
第四步:选择当前权值最小的两个结点,生成新的父结点。
这是对第二步的重复操作。当前队列中权值最小的结点是5和7,生成新的父结点权值是5+7=12:
第五步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列。
这是对第三步的重复操作,也就是从队列中删除5和7,插入12,并且仍然保持队列的升序:
第六步:选择当前权值最小的两个结点,生成新的父结点。
这是对第二步的重复操作。当前队列中权值最小的结点是9和12,生成新的父结点权值是9+12=21:
第七步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列。
这是对第三步的重复操作,也就是从队列中删除9和12,插入21,并且仍然保持队列的升序:
第八步:选择当前权值最小的两个结点,生成新的父结点。
这是对第二步的重复操作。当前队列中权值最小的结点是18和21,生成新的父结点权值是18+21=39:
第九步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列。
这是对第三步的重复操作,也就是从队列中删除18和21,插入39,并且仍然保持队列的升序:
第十步:选择当前权值最小的两个结点,生成新的父结点。
这是对第二步的重复操作。当前队列中权值最小的结点是25和39,生成新的父结点权值是25+39=64:
第十一步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列
这是对第三步的重复操作,也就是从队列中删除25和39,插入64:
此时,队列中仅有一个结点,说明整个森林已经合并成了一颗树,而这棵树就是我们想要的哈夫曼树:
知识点习题
- 有权值分别为11,8,6,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为_____。
A. 24
B. 71
C. 48
D. 53
正确答案: B
答案解析:
- 画出哈夫曼树
(11 + 8 + 6)* 2 + (2 + 5) * 3 = 50 + 21 = 71
32
13 19
6 7 8 11
2 5
- 教大家一个快速解题的方法。特点:不需要画出哈夫曼树就能直接出答案
首先:将权值从小到大排序,然后像下图一样,每次合并的两个节点下面画一个横线,(期间可能要适当的调整结点)
权值的话,就等于所有的结点权值*横线个数之和。
- 给出下述节点及权值(括号中数字为权值),构造huffman树,其带权路径长度为() a(7),b(5),c(4),d(2)
A. 18
B. 35
C. 36
D. 46
正确答案: B
答案解析:
(2 + 4)3 + 52 + 7*1 = 35