E    信息论的概念

本章介绍了信息论的一些基本概念，这些概念有助于介绍 几种学习算法及其性质。定义和定理在 离散随机变量或分布的情况，但它们可以直接扩展到 连续案例。 我们从熵的概念开始，它可以被看作是一个系统不确定性的度量 随机变量。

E.1熵

定义E.1（熵）具有概率质量的离散随机变量 $X$ 的熵

函数 $p(x)=\mathbb{P}[X=x]$ 由 $H(x)$ 表示，定义为

我们用同样的表达式定义了分布 $p$ 的熵，并滥用地表示为 $H(p)$ .

在这个定义中，对数的底不是关键的，因为它只影响一个数值乘法常数。因此，除非另有说明，否则我们将考虑自然对数( $e$ 基)。如果我们使用基数 $2$ ，那么 $\log2(p(x))$ 是表示 $p(x)$ 所需的位数。 因此，根据定义， $X$ 的熵可以被视为平均比特数(或数量) (指信息)用于描述随机变量 $X$ 。通过相同的属性 熵总是非负的：

例如，有偏硬币的熵$Xp$取概率为 $p$ 的值 $1$ 和概率为 $p$ 的值 $0$ 概率 $1∞ p$ 由下式给出

$p$ 的对应函数通常称为二元熵函数。图 $E.1$ 显示使用基数 $2$ 作为对数时该函数的曲线图。从图中可以看出， 熵是一个凹函数。 $26$ 它在 $p=12$ 时达到最大值 ，对应于 最不确定的情况，以及与完全确定的情况相对应的 $p=0$ 或 $p=1$ 时的最小值。 更一般地，假设输入空间 $X$ 具有有限基数 $N≥ 1$ .然后，由詹森的附录 $E$ 信息论的概念。

稍后我们将看到熵函数总是凹的。

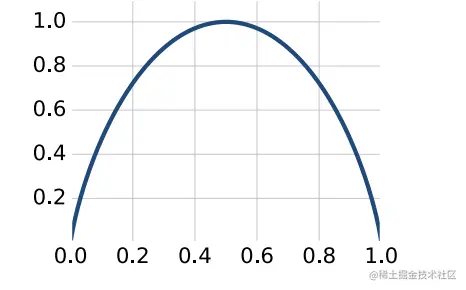
图 $E.1$ 二元熵和偏压 $p$ 的函数关系图
不等式，鉴于对数的凹性，下列不等式成立：

因此，更一般地，熵的最大值是 $logn$ ，即均匀分布。 熵是无损数据压缩的下限，因此是一个临界量 。它还与热力学、动力学和量子物理学中的熵概念密切相关。

E.2相对熵

这里，我们介绍两个分布 $p$ 和 $q$ 之间的散度，相对熵， 这与熵的概念有关。以下是其在离散情况下的定义。 定义 $E.2$ （相对熵）两个粒子的相对熵（或库尔贝克-莱布勒散度） 分布 $p$ 和 $q$ 用 $D（pkq）$ 表示，定义为

按照惯例 $0log0=0$ , $0log\frac{0}{0}=0$ ,和 $alog\frac{a}{0}=+∞对于a>0$

注意，考虑到这些约定，当支持 $p$ 的某些 $x$ 的 $q(x)=0$ 时 $(p(x)>0)$ ，相对熵为无穷大： $D(p||q)=∞$ . 因此，相对熵不存在 在这种情况下，提供 $p$ 和 $q$ 偏差的信息性度量。

至于熵，在相对熵的定义中，对数的底并不重要, 除非另有说明，否则我们将考虑自然对数。如果我们使用基数 $2$ ， 相对熵可以用编码长度来解释。理想情况下，可以为 $p$ 设计 平均长度为熵 $H(p)$ 的最优码。相对熵是平均数 当使用 $q$ 的最佳代码而不是 $p$ 的最佳代码时，编码 $p$ 所需的额外比特数，因为可以表示为差值

如下所示命题，总是非否定的。

命题E.3（相对熵的非负性）对于任意两个分布p和q

以下不平等性：

此外，当 $p=q$ 时， $D(p||q)=0$ 。

证明：根据对数的凹性和 $Jensen$ 不等式，以下结论成立：

因此，对于所有分布 $p$ 和 $q$ ，相对熵总是非负的。平等 $D(p||q)=0$ 仅当上述两个不等式都相等时才成立。最后一个意味着那个 $\sum_{x:p(x)>0}q(x)=1$ 。由于对数函数是严格凹的，第一个不等式可以是 仅当 $\frac{q(x)}{p(x)}$ 时的等式是 {x:p(x)>0} 上的常数α。因为 $p(x)$ 和是一对一, 那一套，我们必须有 $\sum_{x:p(x)>0}q(x)=α$ 。因此, $α=1$ ，这意味着 $q(x)=p(x)\qquad$ x∈ {x:p(x)>0}$，因此对于所有$x$。最后，根据定义，对于任何分布$p$，$D(p||p)=0$ ， 这就完成了证明。

相对熵不是距离。它是不对称的：一般来说， $D(p||q)\neq(q||p)$ 表示两个分布 $p$ 和 $q$ 。此外，一般来说，相对熵不能验证三角形不平等.

E.4 对数和不等式

任意一组非负实数 $a{_1}$ ，…， $a{_n}$ 的推论，和 $b{_1}$ ，…， $b{_n}$ ，以下不等式成立：

按照惯例 $0log0=0$ , $0log\frac{0}{0}=0$ ,和 $alog\frac{a}{0}=+∞$ 对于 $a>0$
此外，在 $(E.7)$ 条中平等是成立的仅在 $\frac{a_i}{b_i}$ 是一个常数(不依赖于i).
证据：随着公约的通过，很明显，如果 $\sum_{i=1}^na_i=0$ 即 $a_i=0$ 对于 $i\in\mathcal [n]$ 或者 $\sum_{i=1}^nb_i=0$ 对所有$i\in\mathcal[n]$. 因此我们可以假设 $\sum_{i=1}^na_i\neq0$ 和 $\sum_{i=1}^nb_i\neq0$. 由于不等式通过 $a_is$ 或 $b_is$ 的标度是不变的，我们可以将它们乘以正常数这样$\sum_{i=1}^na_i=\sum_{i=1}^nb_i=1$ 那么不平等呢?与由此定义的分布的相对熵的非负性一致 $a_is$ 和 $b_is$ 以及命题 $E.3$ 得出的结果。

推论E.5（相对熵的联合凸性）

相对熵函数 $(p，q)\mapsto D (p||q)$ 它是凸的。
证据：任何 $α ∈ [0, 1]$ 和任意四个概率分布 $p_1，p_2，q_1，q_2$ ，通过对数和不等式（推论 $E.4$ ），对于任何固定的 $x$ ，下列等式成立：

总结所有 $x$ 收益率的这些不等式：

这就是证据的结论。

推论E.6（熵的凹性）

熵函数 $P\mapsto H（p）$ 是凹的.
证明：对于 $X$ 上的任何固定分布 $p_0$ ，根据相对熵的定义，我们可以写作

因此， $H(p)=-D(p||p_0)-\sum_{x\in\mathcal X}p(x)log\big(p_0(x)\big)$.根据推论 $E.5$ ，第一项是凹项 $p$ 。第二项在 $p$ 中是线性的，因此是凹的。因此， $H$ 作为 $a$ 是凹的两个凹函数之和。

命题E.7（Pinsker不等式）

对于任意两个分布 $p$ 和 $q$ ，以下不等式成立：

证据：