翻译2

用户105091145635
88 阅读10分钟

第11章回归

本章深入讨论回归的学习问题，其中包括使用数据尽可能的接近预测所考虑的点或项目的正确实值标签。回归是机器学习中的一项常见任务，有着广泛的应用。这就证明了我们对其分析保留的具体章节是正确的。

前几节介绍的学习保证主要集中在分类问题上。这里我们给出了有限和无限假设集回归的推广界。这些学习界中的几个是基于熟悉的Rademacher复杂性概念,这对于描述回归中假设集的复杂性也很有用。另一些是基于为回归量身定制的复杂度组合概念，我们将引入假想维度，这可以看作是VC维度到回归的扩展。基于伪维数的概念，我们描述了一种将回归问题简化为分类并导出泛化界的通用技术。我们提出并分析了几种回归算法，包括线性回归、核岭回归、支持向量回归、Lasso以及这些算法的几种线性版本。我们详细讨论了这些算法的性质，包括相应的学习保障。

11.1回归问题

  1. 我们首先介绍回归的学习问题,设X\mathcal{X}表示输入空间，Y\mathcal{Y}表示R\mathbb{R}的可测子集。在这里我们将采用随机方案，并用D\mathcal{D}表示X×Y\mathcal{X} \times \mathcal{Y}的分布。如第2.4.1节所述，确定性场景是一个简单的特殊情况，其中输入点允许目标函数f:X→Yf:\mathcal{X} \to \mathcal{Y}删除其它标签。

  2. 与所有有监督的学习问题一样，学习者收到一个通过D\mathcal{D}标记的样本 S=((x1,y1),...,(xm,ym))∈(X×Y)m\mathcal{S}=((x_1,y_1),...,(x_m,y_m)) \in (\mathcal{X} \times \mathcal{Y})^m绘制的i.i.d。由于标签是实数，因此希望学习者能够准确预测唯一的正确标签或准确预测其平均标签是不合理的。而不是,我们可以要求的它的预测可以很接近正确的预测。这就是回归和分类的关键区别——误差的度量，它基于实值标签预测值与真实或正确标签预测值之间差异的大小，而不是基于这两个值的相等或不相等。我们用 L:Y×Y→R+L:\mathcal {Y} \times \mathcal{Y} \to \mathbb{R_+} 表示用于测量误差大小的损失函数。回归中最常用的损失函数是平方损失L2L_2,由L(y,y′)=∣y′−y∣2L (y,y')=|y'-y|^2 定义,用于所有yy，y′∈Yy'\in \mathcal{Y}，或者，更一般地说，对于某些 p⩾1\mathcal{p}\geqslant 1和所有y,y′∈Yy,y' \in \mathcal{Y},由L(y,y′)=∣y′−y∣pL(y,y')=|y'-y|^p定义了一个LpL_p损失。

  3. 给出了一个假设集H\mathcal{H}的函数映射X\mathcal{X}到Y\mathcal{Y},回归问题包括使用带标签的样本S\mathcal{S}找到一个假设h∈Hh \in \mathcal{H}，该假设h∈Hh \in \mathcal{H}相对于目标ff具有较小的预期损失或泛化误差R（h）R（h）：

\qquad\qquad\qquad\qquad\qquad R(h) =\underset {(x,y) \sim \mathcal{D}} \mathbb{E} [L(h(x),y)] \qquad\qquad\qquad\qquad\qquad\qquad(11.1)

如前几章所述，h∈Hh \in \mathcal {H}的经验损失或误差用R^s(h)\widehat{R}_s(h)表示，并用公式定义，该公式为：

R^s(h)⩽=1m∑i=1mL(h(xi),yi)(11.2) \qquad\qquad\qquad\qquad\qquad \widehat{R}_s(h) \leqslant=\frac{1}{m} \sum_{i=1}^m L(h(x_i),y_i) \qquad\qquad\qquad\qquad\qquad\qquad(11.2)

在LL为平方损失的常见情况下，这表示样本SS上hh的均方误差。

  1. 当损失函数LL有界于某个M>0M>0时，对所有y,y′∈Yy,y' \in \mathcal{Y}来说，即L(y′,y)⩽ML(y',y) \leqslant M，或者更严格地表达，对于所有h∈Hh \in \mathcal{H}，(x,y)∈X×Y(x,y) \in \mathcal{X} \times \mathcal{Y}来说L(h(x),y)⩽ML(h(x),y) \leqslant M,该问题称为有界回归问题。以下章节中给出的许多理论结果都基于该假设。无界回归问题的分析在技术上更为复杂，通常需要一些其他类型的假设。

11.2一般化界限

本节介绍有界回归问题的学习保证。我们从有限假设集的简单情况开始。

11.2.1有限假设集

在有限假设的情况下，我们可以通过直接应用Hoeffding不等式和并集界导出回归的推广界。

定理11.1

设LL为有界损失函数。假设假设集H\mathcal{H}是有限的。然后，对于任何大于δ>0\delta>0的情况，概率至少为1-δ\delta，以下不等式适用于所有h∈Hh \in \mathcal{H}:

R(h)⩽R^s(h)+Mlog⁡∣H∣+log⁡1δ2mR(h) \leqslant \widehat{R}_s(h)+M \sqrt{\frac{ \log|\mathcal{H|+}\log\frac{1}{\delta}}{2m}}

证明：根据霍夫丁不等式，因为LL取[0,MM]中的值，对于任何h∈Hh \in \mathcal{H}，以下公式成立:

P[R(h)−R^s(h)>ϵ]⩽e−2mϵ2M2\mathbb{P}[R(h)-\widehat{R}_s(h)>\epsilon] \leqslant e^{-\frac{2m\epsilon^2}{M^2}}

因此受到工会的约束。我们可以写为：

P[∃h∈H:R(h)−R^s(h)>ϵ]⩽∑h∈HP[R(h)−R^s(h)>ϵ]⩽∣H∣e−2mϵ2M2\mathbb{P}[\exists h \in \mathcal{H}:R(h)-\widehat{R}_s(h)>\epsilon]\leqslant \sum_{h \in \mathcal{H}} {\mathbb{P} [R(h)-\widehat{R}_s(h)>\epsilon] } \leqslant|\mathcal{H}| e^{-\frac{2m\epsilon^2}{M^2}}

将右手边设为等于δ\delta，就得到了定理的陈述。使用相同的假设和相同的证明，可以导出一个双边界：对于所有h∈Hh \in \mathcal{H}，概率至少为1-δ\delta,

∣R(h)−R^s(h)∣⩽Mlog⁡∣H∣+log⁡2δ2m|R(h)-\widehat{R}_s(h)|\leqslant M \sqrt{\frac{\log|\mathcal{H}|+\log\frac{2}{\delta}}{2m}}

这些学习边界类似于为分类推导的边界。事实上当M=1时，它们与在不一致的情况下给出的分类界限一致。因此，在该上下文中所作的所有注释在此应用相同。特别是较大的样本量m\mathcal{m}保证了更好的泛化；该界限随着对数∣H∣|\mathcal{H}|的增加而增加，并建议为相同的经验误差选择一个较小的假设集。这是Occams razor回归原理的一个实例。在下一节中，我们将使用Rademacher复杂性和伪维的概念，在无限假设集的一般情况下介绍该原理的其他实例。

11.2.2 Rademacher复杂度界限

这里，我们展示了定理3.3的Rademacher复杂度界如何用于推导LpL_p损失函数族回归的推广界。我们首先给出了相关函数族的Rademacher复杂度的上界。

提案11.2（μ−Lipschitz\mu-Lipschitz 损失函数的Rademacher复杂性）

设L:Y×Y→RL:\mathcal{Y} \times \mathcal{Y} \to \mathbb{R}为非负损失上界MM>0 （对于所有y,y′∈Y来说，L（y，y′）⩽M)（对于所有y,y' \in \mathcal{Y}来说，L（y，y'）\leqslant M)，并且对于任何固定的y′∈Yy' \in \mathcal{Y},对于某些μ\mu>0来说，y↦L(y,y′)y \mapsto L(y,y')为μ−Lipschitz\mu-Lipschitz。然后，对于任何样本S=((x1,y1),...,(xm,ym))S=((x_1,y_1),...,(x_m,y_m))，族G\cal{G}={(x,y)↦L(h(x),y):h∈H(x,y)\mapsto L(h(x),y):h \in \mathcal{H}}的RademacherRademacher复杂度为上界，如下所示:

R^s(G)⩽μR^s(H)\widehat{\frak{R}}_s(\cal{G}) \leqslant \mu \widehat{\frak{R}}_s(\mathcal{H})

证明：因为对于任何固定的yi，y↦L（y，yi）y_i，y \mapsto L（y，yi）是μ−Lipschitz\mu-Lipschitz，由TalagrandTalagrand的收缩矩阵（引理，5.7）。我们可以写

\widehat{R}_s(\cal{G})=\frac{1}{m} \underset \sigma \mathbb{E}[\sum_{i=1}^{m}\sigma_i \mathit{L} (h(x_i),y_i)]\leqslant \frac{1}{m} \underset \sigma \mathbb{E}[\sum_{i=1}^{m} \sigma_i \mu h(x_i)]=\mu \widehat{R}_s(\cal{H})

来完成证明。

定理11.3（Rademacher复杂度回归界）

设L:Y×Y→RL:\mathcal{Y} \times \mathcal{Y} \to \mathbb{R} 是一个非负损失上界，M>0(L（y，y′）⩽MM>0(L（y，y'） \leqslant M表示所有y，y′∈Yy，y' \in \mathcal{Y}），因此对于任意的y′∈Y，y↦L（y，y′）y' \in \mathcal{Y}，y \mapsto L（y，y'）证明：因为对于任何固定的yi，yhl（y，3i）是u-lipschitz，由Talagrand的收缩矩阵（引理5.7），我们可以写对于某些μ\mu>0是（μ−Lipschitz\mu-Lipschitz）。

\underset{(x,y) \sim \mathcal{D}} \mathbb{E}[\mathit{L}(x,y)]\leqslant \frac{1}{m} \sum_{i=1}^m \mathit{L}(x_i,y_i)+2\mu \frak{R}_m(\mathcal{H})+M\sqrt{\frac{\log{\frac{1}{\sigma}}}{2m}}
\underset{(x,y) \sim \mathcal{D}} \mathbb{E}[\mathit{L}(x,y)]\leqslant \frac{1}{m} \sum_{i=1}^m \mathit{L}(x_i,y_i)+2\mu \frak{R}_m(\mathcal{H})+3M\sqrt{\frac{\log{\frac{2}{\sigma}}}{2m}}

证明：因为对于任何固定的证明：y′，y↦L（y，yi）y'，y \mapsto L（y，y_i）是μ−Lipschitz\mu-Lipschitz，由TalagrandTalagrand的收缩矩阵（引理5.7），我们可以写

\widehat{R}_s(\cal{G})=\frac{1}{m} \underset \sigma \mathbb{E}[\sum_{i=1}^{m}\sigma_i \mathit{L} (h(x_i),y_i)]\leqslant \frac{1}{m} \underset \sigma \mathbb{E}[\sum_{i=1}^{m} \sigma_i \mu h(x_i)]=\mu \widehat{R}_s(\cal{H})

将该不等式与定理3.3的一般 RademacherRademacher复杂度学习界结合起来完成了证明。

设p⩾1p\geqslant 1,并假设∣h(x)−y∣⩽M|h(x)-y| \leqslant M对于所有（x，y）∈X×Y（x，y）\in\mathcal{X} \times \mathcal{Y}和h∈Hh \in \mathcal{H}，那么，由于对于任何y′y'，函数y↦∣y−y′∣py \mapsto|y-y'|^p对于（y−y′∈[−M,M]（y-y'\in[-M,M]是pMp−1−LipschitzpM^{p-1}-Lipschitz，该定理适用于任何LpL_p损失。例如，对于任何μ\mu>0，在大小为mm的样本SS上概率至少为1-δ\delta的情况下，以下不等式中的每一个都适用于所有h×Hh \times \mathcal{H} ：

\underset{(x,y) \sim \mathcal{D}} \mathbb{E}[|h(x)-y|^p] \leqslant \frac{1}{m} \sum_{i=1}^m|h(x_i),y_i|^p+2pM^{p-1} \frak{R}_m(\mathcal{H})+M^p\sqrt{\frac{\log{\frac{1}{\sigma}}}{2m}}

与分类的情况一样，这些泛化范围表明了在减少经验误差（可能需要更复杂的假设集）和控制H\mathcal{H}的RademacherRademacher复杂性（可能增加经验误差）之间的权衡。定理的最后一个学习界的一个重要优点是它依赖于数据。这可以带来更准确的学习保证。基于核的假设（定理6-12）的Rm(H)\frak{R}_m(\mathcal{H})或Rs(H)\frak{R}_s(\mathcal{H})上界可直接用于推导基于核矩阵轨迹或最大对角项的推广界。

11.2一般化界限

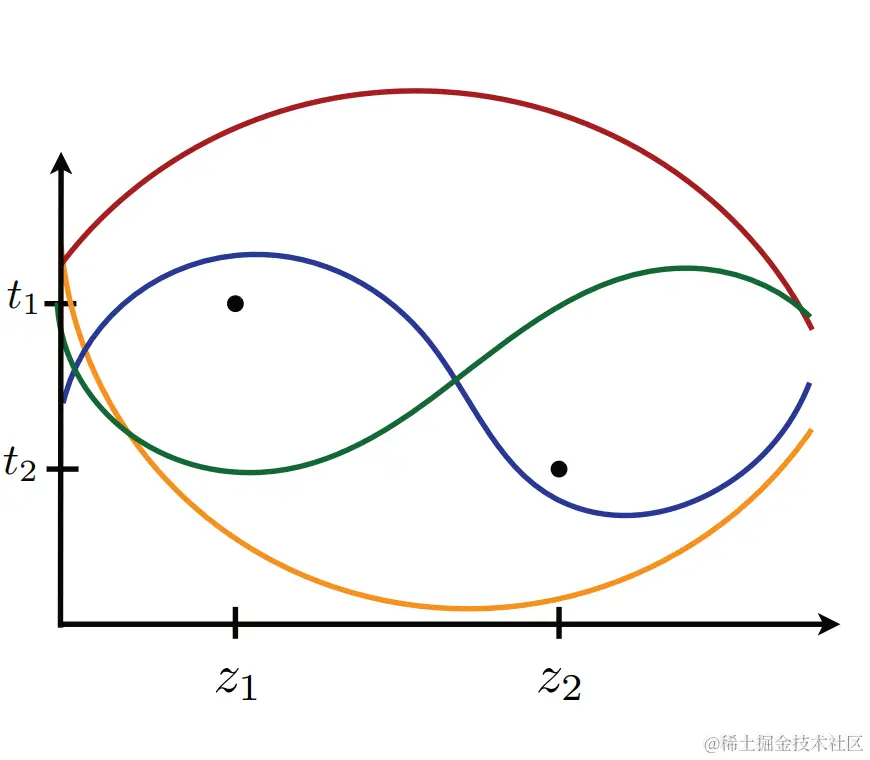
image.png

图11.1

带见证人t1t1和t2t2的一组两点{z1,z2{z_1,z_2}}破碎的图示

11.2.3伪尺寸界限

正如前面在分类案例中所讨论的，有时在计算上很难估计假设集的经验Rademacher复杂性。在第3章中，我们介绍了假设集复杂性的其他度量，如VC\rm{VC}-dimension，它们纯粹是组合的，通常更容易计算或上界。然而，为二元分类引入的破碎或VC\rm{VC}-dimension的概念并不适用于实值假设。

我们首先为实值函数族引入一个新的破碎概念。与前几章一样，我们将使用符号G\cal{G}表示函数族，当我们打算稍后将其解释为（至少在某些情况下）与某个假设集H:G\mathcal{H}:\cal{G}={z=(x,y)↦L(h(x),y):h∈Hz=(x,y) \mapsto L(h(x),y):h \in \mathcal{H}}相关联的损失函数族时。

定义11。4（破碎）

设G\cal{G}是从集合ZZ到R\mathbb{R}的函数族。如果存在t1,...,tm∈Rt_1,...,t_m \in \mathbb{R}，则称一组{z1,...,zm}\{z_1,...,z_m\}被R\mathbb{R}粉碎，从而

∣{[sgn(g(z1)−t1⋮sgn(g(zm)−tm)]:g∈G}∣=2m\begin{vmatrix} \begin{Bmatrix} \begin{bmatrix} sgn(g(z_1)-t_1\\ \vdots \\ sgn(g(z_m)-t_m) \end{bmatrix}:g \in \cal{G} \end{Bmatrix} \end{vmatrix}=2^m

当它们存在时，阈值{t1，…，tm}\{t_1，…，t_m\}被称为见证了破碎。因此，{z1，…，zm}\{z_1，…，z_m\}被破碎，如果对于一些见证者{t1，…，tm}\{t_1，…，t_m\}，函数族G\cal{G}足够丰富，包含一个在点集J={(zi,ti):i∈[m]}\cal{J}=\{(z_i,t_i):i \in [m]\}的子集A\mathcal{A}之上而在其他点集（J−A\cal{J}-\mathcal{A}）之下的函数，对于子集nathcalAnathcal{A}的任何选择。图11。1用一个简单的例子说明了这一点。自然破碎的概念导致了以下定义。

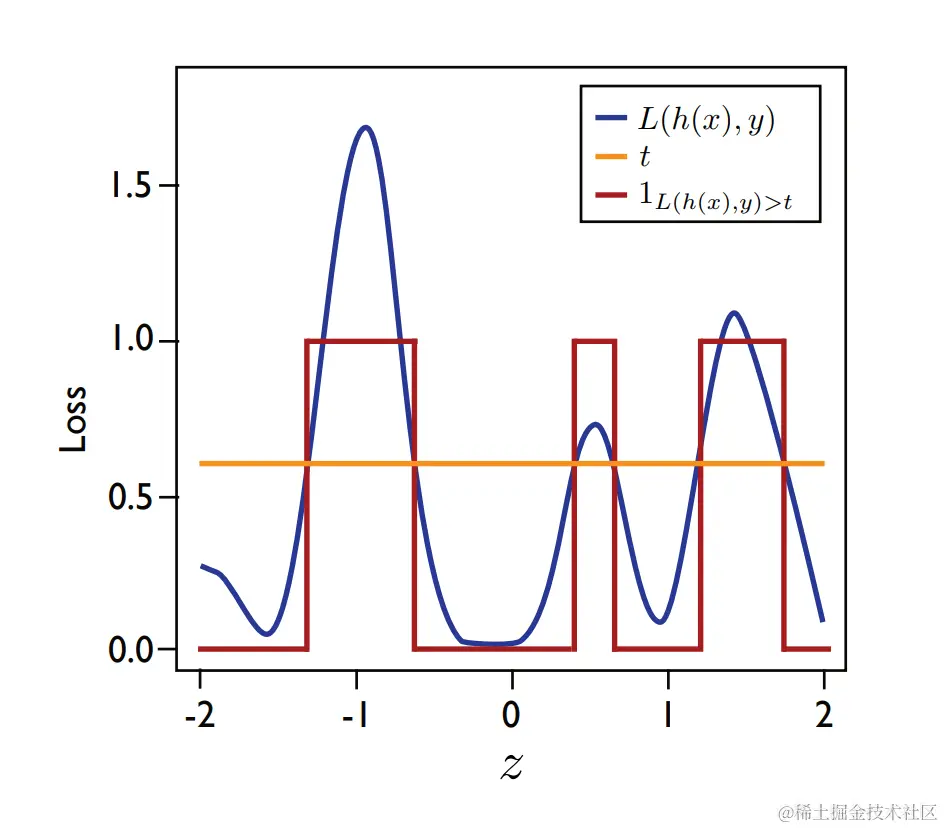
image.png

图11。2.

函数g:z=(x,y)↦L(h(x,y))g:z=(x,y)\mapsto L(h(x,y))(蓝色）定义为关于阈值tt（黄色）的某个固定假设h∈Hh \in \mathcal{H}及其阈值版本(x,y)↦1L(h(x),y)(x,y) \mapsto 1_{L(h(x),y)}（红色）的损失。

定义11.5（伪尺寸）

设G\cal{G}是从X \mathcal{X}映射到R\mathbb{R}的函数族。然后，G\cal{G}的伪维数，用PdimPdim（G\cal{G}）表示，是G\cal{G}破坏的最大集的大小

根据刚才介绍的破碎的定义，实值函数族G\cal{G}的伪维数的概念与对应的阈值函数映射X\mathcal{X}到{0,1}的VC−dimention\rm{VC-dimention}的概念一致

Pdim(G)=VCdim({(x,t)↦1(g(x)−t)>0:g∈G})(11.3)\rm{Pdim}(\mathcal{G})=\rm {VCdim} \left(\{(x,t) \mapsto 1_{(g(x)-t)>0}:g \in \mathcal{G}\}\right) \qquad\qquad\qquad(11.3)

图11.2说明了这种解释。鉴于这种解释，以下两个结果直接遵循VCVC维度的特性

定理11.6 RN\mathbb{R}^N中超平面的伪维数由下式给出

Pdim({x↦w⋅x+b:w∈RN,b∈R})=N+1Pdim(\{\bf{x} \mapsto \bf{w \cdot x}+\rm{b}:\bf{w} \in \mathbb {R}^{\rm{N}} ,\rm{b}\in \mathbb{R} \})=N+1

定理11.7实值函数H\cal{H}的向量空间的伪维数等于向量空间的维数:

Pdim(H)=dim(H)\rm{Pdim}(\mathcal{H})=dim(\mathcal{H})

以下定理根据损失函数族G={z=(x,y)↦L(h(x),y):h∈H}\mathcal{G}=\{z=(x,y) \mapsto L(h(x),y):h \in \mathcal{H}\}的伪维数给出了有界回归的推广界与假设集H\mathcal{H}相关。推导这些界限的关键技术包括利用以下关于随机变量XX期望的一般恒等式，将问题简化为分类问题:

E[X]=−∫−∞0P[X<t]dt+∫0+∞P[X>t]dt,(11.4)\qquad\qquad\qquad\mathbb{E}[X]=-\int_{- \infty}^0 \mathbb{P}[X<t]dt+\int_0^{+ \infty} \mathbb{P}[X>t]dt,\qquad\qquad\qquad(11.4)

11.2一般化界限

根据勒贝格积分的定义，它成立。特别地，对于任何分布D\mathcal{D}和任何非负可测函数ff，我们可以写

\qquad\qquad\qquad\underset{z \sim \mathcal{D}}\mathbb{E}[f(z)]=\int_0^\infty \underset{z \sim \mathcal{D}}\mathbb{P} [f(z)>t]dt.\qquad\qquad\qquad\qquad\qquad\qquad(11.5)

定理11.8

设H\mathcal{H}是实值函数族，G={(x，y）↦L(h(x,y)):h∈H}\cal{G}=\{(x，y）\mapsto \it{L} (h(x,y)):h \in \cal{H} \}是与H\mathcal{H}相关联的损失函数族。假设Pdim(G)=dPdim (\cal{G})=d，且损失函数LL是非负的且有界于MM。然后，对于任何δ>0\delta>0，在选择从Dm\cal{D}^m提取的MM大小的am i.i.di.i.d.样本SS时，概率至少为1−δ1-\delta，以下不等式适用于所有h∈Hh \in \cal{H}:

R(h)⩽R^s(h)+M2dlog⁡emdm+Mlog⁡1δ2m(11.6)\qquad\qquad\qquad R(h)\leqslant \widehat{R}_s(h)+M \sqrt{\frac{2d \log{\frac{em}{d}}}{m}}+M \sqrt{\frac{\log{\frac{1}{\delta}}}{2m}}\qquad\qquad\qquad\qquad(11.6)

证明：让我们做一个尺寸为 mm的样品，绘制i.i.d。根据D \cal{D}，让D^\widehat{\cal{D}}表示由SS定义的经验分布。对于任何h∈Hh \in \cal{H}和t⩾0t \geqslant 0，我们用c（h，t）表示由c(h,t)定义的分类:(x,y)↦1L(h(x),y)>t(x,y) \mapsto 1_{L(h(x),y)>t}的误差可由以下公式定义：

R(c(h),t)=P(x,y)∼D[c(h,t)(x,y)=1]=P(x,y)∼D[L(h(x),y)>t],R(c(h),t)=\underset{(x,y) \sim{\mathcal{D}}}{\mathbb{P}}[c(h,t)(x,y)=1]=\underset{(x,y) \sim{\mathcal{D}}}{\mathbb{P}}[L(h(x),y)>t],

并且，同样地。其经验误差为：R^s(c(h,t))=R(x,y)∼D^[L(h(x),y)>t]\widehat{R}_s(c(h,t))=\cal{R}_{(x,y) \sim \widehat{\cal{D}}} [\rm{L}(h(x),y)>t]

现在，考虑到恒等式（11.5）和损失函数LL以MM为界的事实，我们可以写

∣R(h)−R^s(h)∣=∣E(x,y)∼D[L(h(x),y]−E(x,y)∼D^[L(h(x),y)]∣ =∣∫0M(P(x,y)∼D[L(h(x),y)>t]−P(x,y)∼D^[L(h(x),y)>t])dt∣⩽Msupt∈[0,M]∣P(x,y)∼D[L(h(x),y)>t]−P(x,y)∼D^[L(h(x),y)>t]∣=Msupt∈[0,M]∣R(c(h,t))−R^s(c(h,t))∣|R(h)- \widehat{R}_s(h)| =\begin{vmatrix} \underset{(x,y) \sim{\mathcal{D}}}{\mathbb{E}}[L(h(x),y]-\underset{(x,y) \sim{ \widehat{\mathcal{D}}}}{\mathbb{E}}[L(h(x),y)] \end{vmatrix}\qquad\qquad\qquad \\ \qquad\qquad\qquad\qquad\ =\begin{vmatrix} \int_0^M \begin{pmatrix} \underset{(x,y) \sim{\mathcal{D}}}{\mathbb{P}}[L(h(x),y)>t]-\underset{(x,y) \sim{ \widehat{\mathcal{D}}}}{\mathbb{P}}[L(h(x),y)>t] \end{pmatrix} dt \end{vmatrix} \\ \qquad\qquad\qquad\qquad \leqslant M \underset{t \in[0,M]}{sup} \begin{vmatrix} \underset{(x,y) \sim{\mathcal{D}}}{\mathbb{P}}[L(h(x),y)>t]-\underset{(x,y) \sim{ \widehat{\mathcal{D}}}}{\mathbb{P}}[L(h(x),y)>t] \end{vmatrix}\\ = M \underset{t \in[0,M]}{sup} \begin{vmatrix} R(c(h,t))-\widehat{R}_s(c(h,t)) \end{vmatrix}\qquad

这意味着以下不平等

P[suph∈H ∣R(h)−R^s(h)∣>ϵ]⩽P[suph∈Ht∈[0,M] ∣R(c(h,t))−R^s(c(h,t))∣>ϵM]\mathbb{P} \begin{bmatrix} \underset{h \in \cal{H}}{sup} \ |R(h)- \widehat{R}_s(h)|> \epsilon \end{bmatrix} \leqslant \mathbb{P} \begin{bmatrix} \underset{\underset{t \in[0,M]}{h \in \cal{H}}}{sup} \ \begin{vmatrix} R(c(h,t))- \widehat{R}_s(c(h,t)) \end{vmatrix}> \frac{\epsilon}{M} \end{bmatrix}

根据hy−potheseshy-potheses族的VCVC维，可以使用分类的标准泛化界（推论3.19）对右侧进行界定

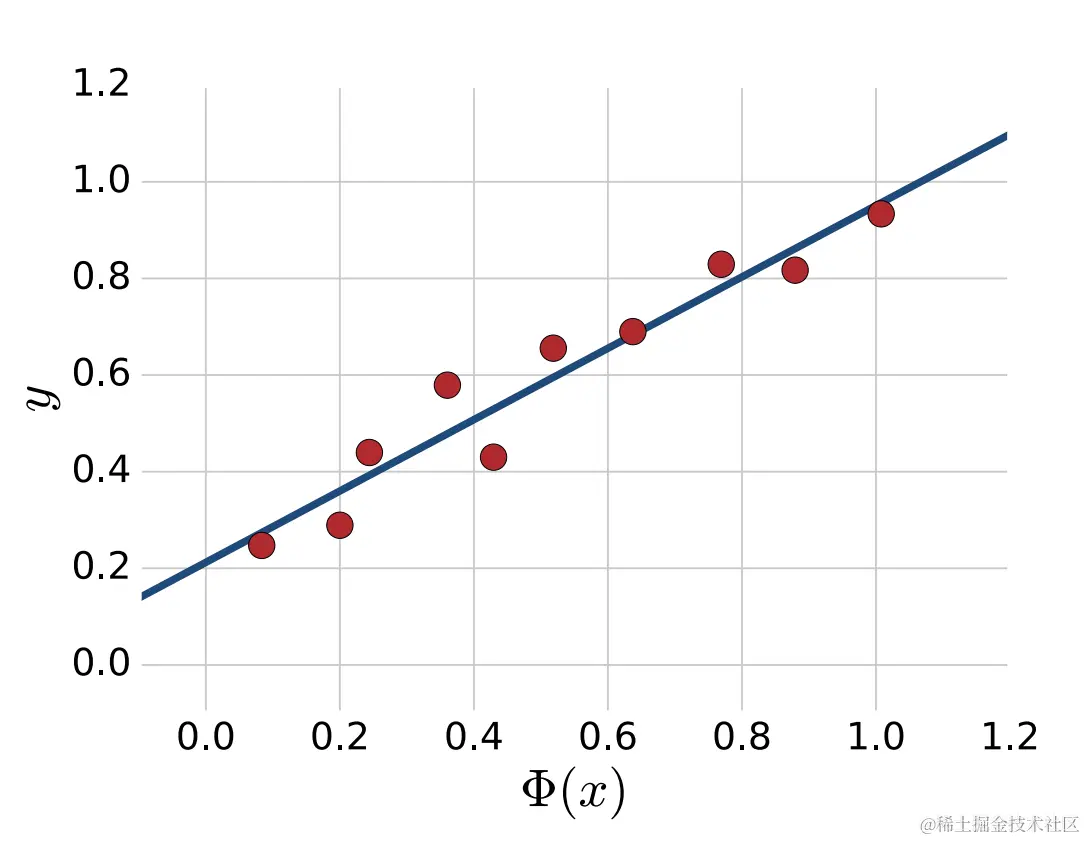
image.png

图形11.3

对于N=1N=1，线性回归包括找到最佳拟合线，以损失平方衡量。

{c(h,t):h∈H,t∈[0,M]c(h,t):h \in \cal{H}, t \in[0,\it{M}]}，根据伪维数的定义，它精确地表示为Pdim（G）=dPdim（\cal{G}）=d。所得界限与（11.6）一致

如前一定理所示，伪维数的概念适用于回归分析；然而，这不是一个规模敏感的概念。存在另一种复杂性度量，脂肪粉碎维度，即规模敏感性，可以被视为伪维度的自然扩展。其定义基于γ\gamma粉碎的概念。

定义11.9（γ\gamma-破碎）

设G\cal{G}是从Z\cal{Z}到R\mathbb{R}的一个函数族，γ\gamma>0一个集合{z1,...,zmz_1,...,z_m}⊆X\subseteq \cal{X}被G\cal{G}打碎，如果存在t1,...,tm∈Rt_1,...,t_m \in \mathbb{R}，那么对于所有y∈{−1,+1}m\rm{y} \in \{-1,+1\}^m，存在g∈Gg \in \cal{G}，这样

Vi∈[M],yi(g(zi)−ti)⩾γV_i \in[M],y_i(g(z_i)-t_i) \geqslant \gamma

因此，{z1,...zm}\{z_1,...z_m\}是γ\gamma-破碎的，如果对于一些证人t1,...,tmt_1,...,t_m，函数族G\cal{G}足够丰富，对于子集a的任何选择，它至少包含一个在点集J={(zi,ti):i∈[M]} \cal{J}=\{(z_i,t_i):i \in[\it{M}]\}的子集a上方γ\gamma且在其他(G−A\cal{G}-\cal{A})下方γ\gamma的函数。

定义11.10（γ\gamma-fat维度）

G\cal{G}的gammagamma-fat维数，fatγGfat_{\gamma} \cal{G}，是由G\cal{G}分解的最大集的大小。

根据γ\gamma-fat-dimension可以导出比基于伪维的更精细的泛化边界。然而，由此产生的学习范围并不比基于Rademacher复杂度的学习范围更具信息量，Rademacher复杂度也是一种尺度敏感的复杂度度量。因此，我们将不详述基于γ\gamma-fat维度的分析。

11.3回归算法

前几节的结果表明，对于相同的经验误差，根据Rademacher复杂度或伪维数测量的复杂度较小的假设集受益于更好的泛化保证。一类复杂度相对较小的函数是线性假设。在本节中，我们描述并分析了基于该假设集的几种算法：线性回归、核岭回归（KRR）、支持向量回归（SVR）和套索。这些算法，特别是最后三种，在实践中得到了广泛的应用，通常会产生最先进的性能结果。

11.3.1线性回归

我们从最简单的回归算法开始，称为线性回归。设Φ:X→RN\Phi:\cal{X} \to \mathbb{R}^{\rm{N}}是从输入空间X\cal{X}到RN\mathbb{R}^N的特征映射，并考虑线性假设族。

H={x↦w⋅Φ(x)+b:w∈RN,b∈R}(11.7)\qquad\qquad\qquad\cal{H}=\{x \mapsto \bf{w \cdot \Phi}(x)+b:\bf{w} \in\mathbb{R}^N,b \in \mathbb{R} \} \qquad\qquad\qquad\qquad (11.7)
minw,b 1m∑i=1m(w⋅Φ(xi)+b−yi)2.(11.8) \qquad\qquad\qquad \underset{\bf{w},\rm{b}}{\rm{min}} \ \frac{1}{m} \sum_{i=1}^m(\bf{w \cdot \Phi}(x_i)+\rm{b}-y_i)^2 . \qquad\qquad\qquad\qquad \qquad\qquad (11.8)
minW F(W)=1m∥XTW−Y∥2(11.9)\qquad\qquad\qquad \underset{\bf{W}}{min} \ F(\bf{W})=\rm{\frac{1}{m}} \begin{Vmatrix}{\bf{X}^T \bf{W}-\bf{Y}} \end{Vmatrix}^2\qquad\qquad\qquad\qquad \qquad\qquad (11.9)

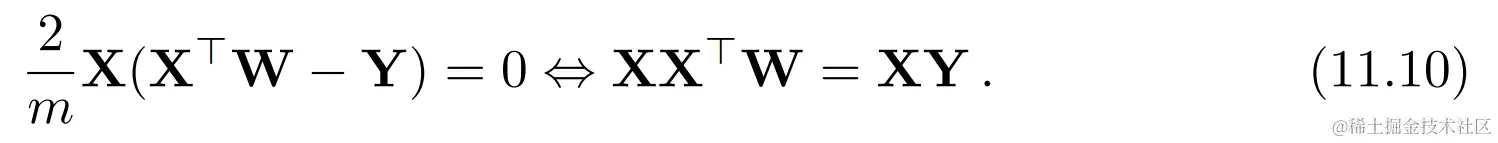
image.png

2mX(XTW−Y)=0\frac{2}{m} \bf{X}(X^{\rm{T}}W-Y)=0
avatar
文章
阅读
粉丝