第7章 Boosting
集成方法是机器学习中的一种通用技术,可以去结合多个预测器来创建一个更准确的预测器。本章研究了一个被称为增强的重要集成方法家族,这个方法具体来说就是AdaBoost算法。该算法在某些场景中已经被实践证明是非常有效的,并且是基于丰富的理论分析。我们首先来介绍AdaBoost,展示下它如何通过快速减少轮数增强的经验误差,并指出它与一些著名算法的关系。接下来,我们来呈现出一种基于AdaBoost假设集的vc维数,并对AdaBoost的推广性质进行了理论分析,然后基于边际的概念,对其泛化性质进行了理论分析。在这种情况下发展的边际理论可以应用于其他类似的集成算法。而AdaBoost的博弈论可以进一步有助于分析其性质,揭示了弱学习假设与可分条件的等价性。
7.1 Introduction
这通常是困难的,对于一个不平凡的学习任务,去直接设计出一种满足第2章强PAC学习要求的精确算法。但是,还是有很大的希望去找到仅能保证表现比随机稍好一些的简单预测器。下面给出了这种弱学习者的正式定义。正如在PAC学习的章节中一样,我们设n为一个数字,表示任何元素x∈X的计算代价最多为O(n),并用大小(c)表示c∈C计算表示的最大代价。
定义7.1(Weak learning)
如果存在一个概念类∈C据说是弱PAC可学习的一个算法A,γ>0,和一个多项式函数多聚(·,·,·),这样对于任何σ>0,对于X上的所有分布∈D和任何目标概念c∈C,
AdaBoost(∈S=((x1,y1),...,(xm,ym)
for i←to m do
D1(i)←m1
for t ← 1 to T do
ht←基础分类器H误差小ϵt=ρi Dt[ht(xi)=yi]
at←21logϵt1−ϵt
Zt←[ϵt(1−ϵt)]21⊳ 归一化[标准化]因数
for i ←1 to m doDt(i)←ZtDt(i)exp(−atyiht(xt))
f←∑t=1Tatht
returnf
图7.1基本分类器集H⊆−1,+1x的AdaBoost算法。以下算法适用于任何样本大小的m≥poly(1/σ,n,size(c)):
其中hS是算法A在样本S上训练时返回的假设。当这样的算法A存在时,它被称为C的弱学习算法或弱学习者的算法。弱学习算法返回的假设称为基础分类器。
增强技术背后的关键思想是使用一个弱学习算法来建立一个强的学习者,也就是说,一个精确的PAC学习算法。要做到这一点,提升技术采用了一种集成方法:它们结合了弱学习者返回的不同基础分类器,以创建一个更准确的预测器。但是应该使用哪些基础分类器以及如何组合呢?下一节来通过详细描述一种最普遍和最成功的增强算法,AdaBoost来解决这些问题。
我们用 H 表示从中选择基本分类器的假设集,我们有时会称之为基分类器集。图7.1给出
图7.2
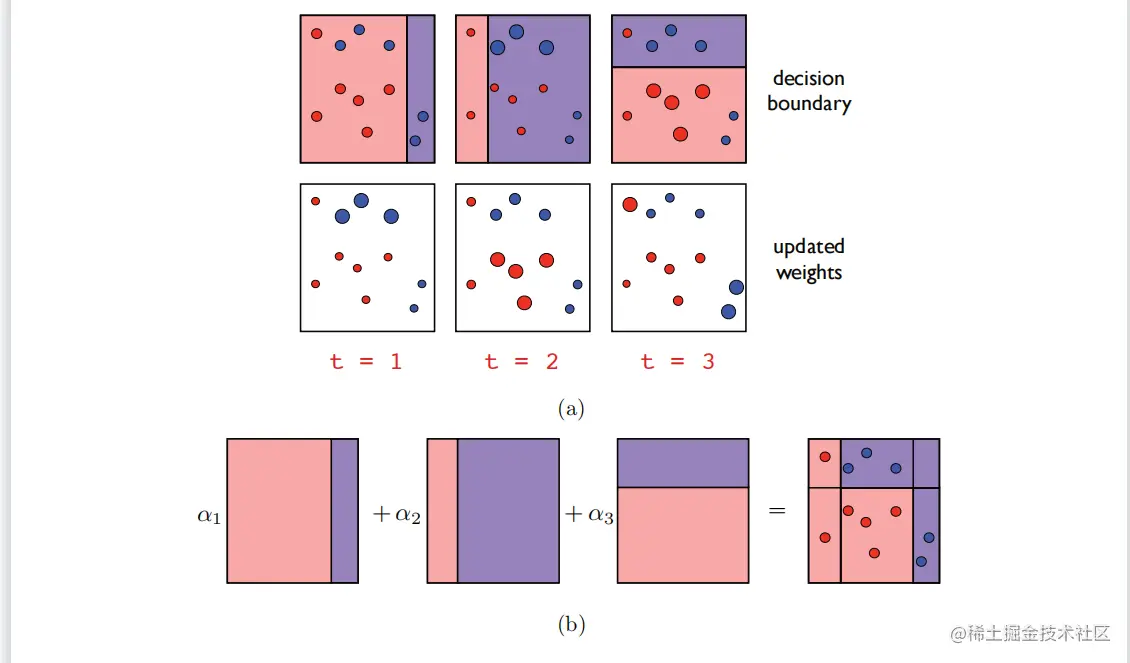 以轴对齐的超平面作为基础分类器的AdaBoost示例。(a)最上面的一行显示了每一轮推进时的决策边界。下面一行显示了每一轮如何更新权重,给出错误(正确)权重增加(减少)。(b)最终分类器的可视化,构造为基分类器的非负线性组合。
在基分类器是从X映射到{−1,+1}的函数时,AdaBoost的伪代码,因此H⊆{−1,+1}X。
该算法以一个标记的样本S=((x1,y1),…,(xm,ym))作为输入,其中,(xi,yi) ⊆X×−1,+1为所有的i∈m,并在索引{1,…,m}上保持一个分布。最初(第1至2行),分布是均匀的(D1)。在每一轮增强h时,即循环3−8的每次迭代t∈i,选择一个新的基分类器t∈H,使由分布Dt加权的训练样本的误差最小化:
以轴对齐的超平面作为基础分类器的AdaBoost示例。(a)最上面的一行显示了每一轮推进时的决策边界。下面一行显示了每一轮如何更新权重,给出错误(正确)权重增加(减少)。(b)最终分类器的可视化,构造为基分类器的非负线性组合。
在基分类器是从X映射到{−1,+1}的函数时,AdaBoost的伪代码,因此H⊆{−1,+1}X。
该算法以一个标记的样本S=((x1,y1),…,(xm,ym))作为输入,其中,(xi,yi) ⊆X×−1,+1为所有的i∈m,并在索引{1,…,m}上保持一个分布。最初(第1至2行),分布是均匀的(D1)。在每一轮增强h时,即循环3−8的每次迭代t∈i,选择一个新的基分类器t∈H,使由分布Dt加权的训练样本的误差最小化:
ht∈h∈Hargmini∼DiP[h(xi)=yi]=h∈Hargmini=1∑mDt(i)h(xi)=yi
zt只是一个归一化因子,以确保权重Dt(i)之和为1。
定义系数αt的确切原因将在稍后变得清楚。
目前,观察到,如果ϵt基分类器的t的误差小于21,这时ϵt1−ϵt>1并且at是积极的(at>0).因此,新的分布Dt+1是从Dt通过大大增加它的重量i如果点xi是错误的分类(yi ht(xi)<0),相反,如果xi是正确分类的。这样做的效果是更多地关注下一轮助推中错误分类的点,而不是那些正确分类的点ht
经过T轮增强后,AdaBoost返回的分类器是基于函数的符号进行的f,这是一个基分类器的非负线性组合ht。重量αt被分配给ht在这个和中是精度之比的对数函数1−ϵt和错误ϵt的ht.因此,更准确的基分类器在这个总和中被分配了一个更大的权重。图7.2说明了AdaBoost算法。这些点的大小表示在每一轮推进时分配给它们的分布权重。任何t∈[T],我们将用ft表示基分类器的线性组合t轮升力:ft=∑s=1tashs。特别是,我们有fT=f分布Dt+1可以用ft归一化因素Zs,s∈[t],如下:
∀i∈[m],Dt+1(i)=m∏s=1tZse−yift(xi) (7.2)
我们将在以下章节的证明中多次使用这个恒等式。它可以通过重复扩展点上分布的定义来直接显示出来xi:
Dt+1(i)=Zte−αtyift(xi)=Zt−1ZtDt−1(i)e−at−1yiht−1(xi)e−atyift(xi)=m∏s=1tZseyi∑s=1tashs(xi)
AdaBoost算法可以通过以下几种方式进行推广:
ht可以不是加权误差最小的假设,而是由训练过的弱学习算法返回的基本分类器Dt;
基分类器的范围可以是[−1.+1],或者更一般地是一个有界的子集R
系数αt可以不同,甚至可能不允许封闭形式。一般来说,选择它们是为了最小化经验误差的上界,如下一节所述。当然,在这种一般情况下,假设ht不是二进制分类器,但它们的符号可以定义标签,它们的大小可以被解释为置信度的度量。
在本章的其余部分中,H中的基分类器的范围将被假设包含在[−1+1]中。我们进一步分析AdaBoost的特性,并讨论其在实践中的典型应用。
7.2.1结合经验误差
我们首先证明了AdaBoost的经验误差随着助推轮数的函数呈指数快速减小.
定理7.2
AdaBoost返回的分类器的经验误差验证了:Rs(f)≤exp[−2t=1∑T(21−ϵt)2]
(7.3)
此外,如果为所有人t∈[T],γ≤(21−ϵt),这时Rs(f)≤exp(-2γ2T).
证明:使用一般的不等式1u≤0≤exp(−u)对所有人都有效u∈R和身份7.2,我们可以写道:
Rs(f)=m1i=1∑myif(xi)≤0 ≤m1
i=1∑m[mt=1∏TZt]{i=1}DT+1=t=1∏TZt
因为所有t∈[T],Zt是一个标准化因子,它可以用ϵt通过:
Zt=i=1∑mDt(i)e−at−1yiht−1(xi)=i:yiht(xi)=+1∑Dt(i)e−at+i:yiht(xi)=−1∑Dt(i)eat
=(1-ϵt)e−at+ϵteαt
=(1-ϵt)1−ϵtϵt+ϵtϵt1−ϵt=2ϵt(1−ϵt)
因此,归一化因子的乘积可以表示和上界如下:
t=1∏TZt=t=1∏T2ϵt(1−ϵt)=t=1∏T1−4(21−ϵt)2≤t=1∏Texp[−2(21−ϵt)2]
=exp[−2(21−ϵt)2]
其中的不等式来自于这个不等式1−x≤e−x对所有人都有效x∈R.□
请注意,γ的值,这被称为边缘,并且算法不需要知道基本分类器的准确性。该算法适应了他们的需求
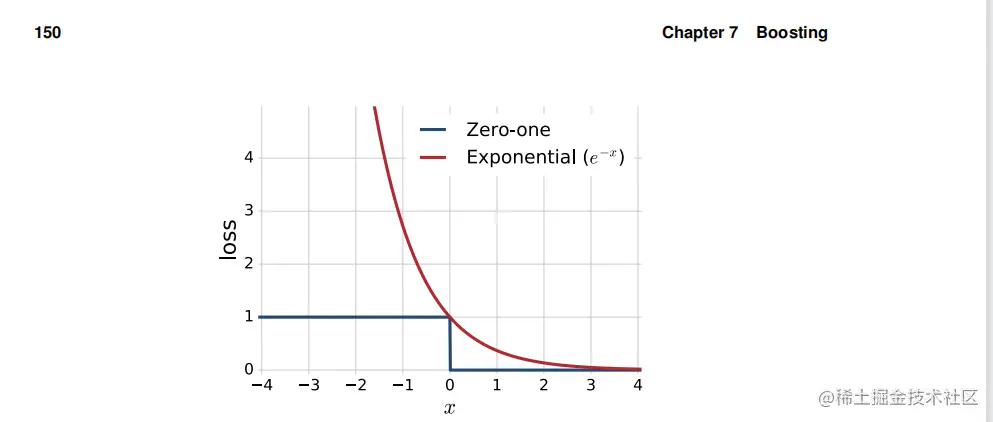
图7.3由AdaBoost优化的零损失(蓝色)和零损失(红色)的凸和可微上界的可视化。并根据这些值定义了一个解决方案。这是AdaBoost的扩展名称的来源:自适应增强。定理7.2的证明揭示了其他几个重要的性质。首先,观察到αt是函数的最小值φ:α↦(1−ϵt)e−α+ϵteα.的确,φ是凸的和可微的,并将其导数设置为零产量: φ(α)=−(1−ϵt)e−α+ϵteα=0⇔(1−ϵt)e−α=ϵteα
图7.3由AdaBoost优化的零1损失(蓝色)和零1损失(红色)的凸和可微上界的可视化。并根据这些值定义了一个解决方案。这是AdaBoost的扩展名称的来源:自适应增强。定理7.2的证明揭示了其他几个重要的性质。首先,观察到αt是函数的最小值φ:α↦(1−ϵt)e−α+ϵteα.的确,φ是凸的和可微的,并将其导数设置为零产量:
φ(α)=−(1−ϵt)e−α+ϵteα=0⇔(1−ϵt)e−α=ϵteα
图7.3由AdaBoost优化的零1损失(蓝色)和零1损失(红色)的凸和可微上界的可视化。并根据这些值定义了一个解决方案。这是AdaBoost的扩展名称的来源:自适应增强。定理7.2的证明揭示了其他几个重要的性质。首先,观察到αt是函数的最小值φ:α↦(1−ϵt)e−a+ϵtea.的确,φ是凸的和可微的,并将其导数设置为零产量:
φ(α)=−(1−ϵt)e−α+ϵtea=0⇔(1−ϵt)e−α=ϵtea⇔a=21logϵt1−ϵt.(7.5)
因此,选择αt来最小化Zt=φ(at)而且,根据这个界限Rs(f)≤∏t=1TZt如图所示,这些系数被选择来最小化经验误差的上界。事实上,对于范围为[−1,+1]或R的基本分类器,αt可以以类似的方式选择来最小化Zt,这就是AdaBoost扩展到这些更一般的情况的方式。还要注意的是,平等的(1−ϵt)e−at=ϵteat如(7.5)所示,在每次迭代中,AdaBoost将等分布质量分配给正确和错误分类的实例,因为(1−ϵt)e−αt是分配给正确分类点的总分布,以及错误分类点的总分布ϵteat。这似乎与AdaBoost增加了错误分类点的权重并减少了其他点的权重的事实相矛盾,但事实上并不一致:原因是错误分类点的权重总是更少,因为基本分类器的准确性比随机的好。
7.2.2与坐标下降AdaBoost的关系最初是为了解决弱学习算法是否可以用来推导出强学习算法的理论问题。在这里,7.2AdaBoost151我们将证明它实际上与一个非常简单的算法一致,该算法包括将一般坐标降技术应用于凸可微目标函数。为简单起见,在本节中,我们假设基分类器集H是有限的,具有基数N:H=(h1,...,hN)。集成函数f比如AdaBoost返回的那个,然后可以被写成f=m1∑j=1Na−jhj,随着a−j ≥0给定一个标记样本S=((x1,y1),...,(xm,ym),设F是为所有对象定义的目标函数a−(a−1,..,a−N)∈RN通过:
F(a−)=f)=m1i=1∑m yif(xi)≤0≤m1i=1∑m e−yif(xi)
F是一个α的一个凸函数,因为它是一个凸函数的和,每个凸函数都是由(凸)指数函数和一个\mathop α的仿射函数组成得到的。F也是可微的,因为指数函数是可微的。我们将证明F是由AdaBoost最小化的目标函数。不同的凸优化技术可以用来最小化f。在这里,我们将使用坐标下降技术的一个变体。坐标下降应用于T轮上。设a−0=0并且设a−t表示迭代结束时的参数向量t。在每一轮t∈[T],方向ek对应的第k个坐标a−在R是选择的,以及一个步长η沿着那个方向.a−t是从a−t−1根据更新a−t=a−t−1+ηek,其中η是沿着ek方向选择的步长。请注意,如果我们用g−t集成函数决定由a−t,即g−t=∑j=1Na−jhj,然后,坐标下降更新与该更新相一致g−t=g−t−1+ηhk,这也是AdaBoost的更新。因此,由于这两种算法都是从g−0=0, ,以表明AdaBoost与坐标下降应用于F,只要在每次迭代中显示出来都足够了t,坐标下降选择相同的基本假设香港和步骤η作为AdaBost提升。我们将通过归纳法假设这适用于迭代t−1,这意味着等式g−t−1=f−t−1然后将显示它在迭代t中也成立。
我们在这里考虑的坐标下降的变体包括,在每次迭代中,选择最大的下降方向,即F的导数是绝对值最大的方向,并沿着该方向选择最好的步骤,即选择η来最小化F(a−t−1+ηek)。为了给出每次迭代的方向和步骤的表达式,我们首先引入第7章152与分析中出现的增强量。任何t∈[T],我们在指数{1,……}上定义了一个分布Dt,如下所示:
D−(i)=Z−te−yif(xi)∑j=1Na−t−1hj(xi)=Z−te−yig−t−1(xi)
其中,Z−t为归一化因子Z−t=∑i=1me−yif(xi)∑j=1Na−t−1hj(xi)。注意,因为g−t−1=f−t−1,D−t与Dt(i)我们也定义了任何基本的假设hj,j∈[N],其预期误差ϵ−t,j关于分布Dt:ϵ−t,j=[1yihj(xi)≤0]
F′的方向导数a−t−1沿着ek被表示为 F(a−t−1,ek)=η→0lim→ηF(a−t−1+ηek)−F(a−t−1)
从F′(a−t−1,ek)=∑i=1me−yi∑j=1Na−t−1hj(xi),沿ek的方向导数可以表示如下:
=−m1i=1∑m yihk(xi)e−yi∑j=1Na−t−1hj(xi)
=−m1i=1∑m hk(xi)D−t(i)Z−t
=-[∑i=1mD−t(i)yihk(xi)=+1−D−t(i)yihk(xi)=−1]mZ−t
从mZ−t不依赖于k,最大下降方向k是一个最小方向ϵt,K因此,迭代t时坐标下降选择的假设hk是样本S上期望误差最小的假设hk,其中期望对D−t=Dt进行。这与AdaBoost在第t轮的选择完全匹配。
选择步长η以沿所选择的方向最小化函数ek:argminηF(a−t−1,ek)自从 F(a−t−1,ek)是η的一个凸函数,以找到
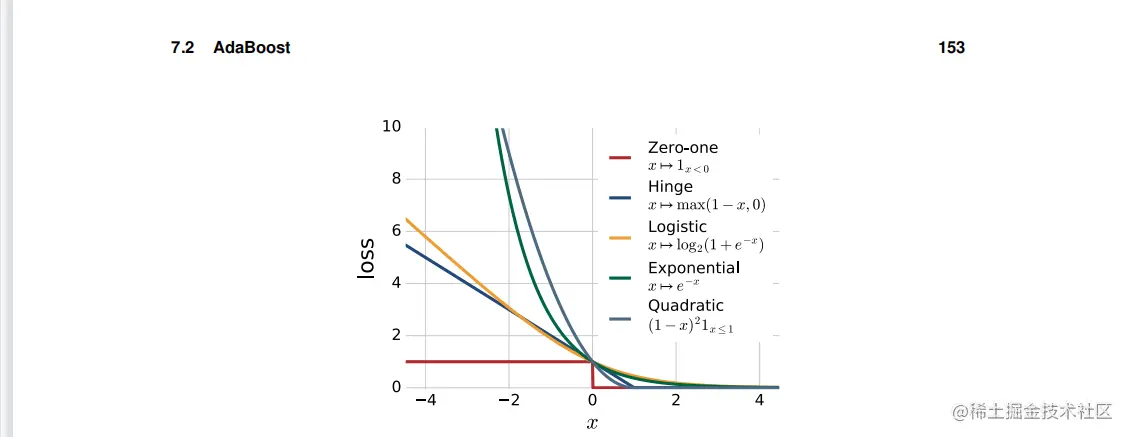
图7.4从损失的几个凸上界的例子的最小值,它足以将其导数设为零:
dηdF(a−t−1,ek)=0⇔m1i=1∑mhk(xi)D−t(i)Z−te−ηyihk(xi)=0
−⇔m1i=1∑mhk(xi)D−t(i)Z−te−ηyihk(xi)=0
−⇔m1i=1∑mhk(xi)D−t(i)e−ηyihk(xi)=0
⇔−[(1−ϵ−t,k)e−η−ϵ−t,keη]=0
⇔η=21logϵ−t,k1−ϵ−t,k
这证明了坐标下降选择的步长与AdaBoost分配给第t轮中选择的分类器的权重αlphat一致。因此,应用于指数目标F的坐标下降与AdaBoost精确重合,而F可以看作是AdaBoost寻求最小化的目标函数。鉴于这种关系,我们可以考虑坐标下降到零损失a−的上界的其他凸可微函数的类似应用。特别是,逻辑损失x⟼log2(1+e−x)是凸的和可微的,是零损失的上界。图7.4显示了具有零损失上限的备选凸损失函数的其他例子。使用逻辑损失,而不是AdaBoost使用的指数损失,会导致一个与逻辑回归相一致的目标。
在这里,我们简要描述了AdaBoost的标准实际应用。该算法的一个重要要求是选择基分类器或弱学习器。在实践中,AdaBoost通常使用的基本分类器家族是决策树,这相当于空间的层次分区(见第9章,第9.3.3节)。在决策树中,深度为1的树,也被称为树桩,是迄今为止最常用的基分类器。提升树桩是与单个特性关联的阈值函数。因此,树桩对应于单个轴对齐的空间分区,如图所示如图7.2所示。如果数据在RN,我们可以将一个残桩与每个N个分量关联起来。因此,为了确定在每一轮推进时具有最小加权误差的树桩,必须计算每个分量的最佳分量和最佳阈值。为此,我们可以首先在O(mlogm)时间内对每个组件进行预排序,总计算成本为O(mlogm)。对于一个给定的组件,只有m+1可能存在不同的阈值,因为相同的连续组件值之间的两个阈值是等价的。为了找到每一轮增压时的最佳阈值,可以比较所有这些可能的m+1值,这可以在O(m)时间内完成。因此,T轮提升算法的总计算复杂度为O(mNlogm+mNT) 。然而,请注意,虽然增强树桩与AdaBoost被广泛使用,并且在实践中表现很好,但以最小(加权)经验误差返回树桩的算法不是一个弱学习者(参见防御7.1)!例如,考虑简单的XOR示例,R2中有四个数据点(见图6.3a),其中第二象限和第四象限的点是正标记的,第一和第三象限的点是负标记的21
7.3在本节中,我们对AdaBoost的推广特性进行了理论分析。7.3.1基于vc维度的分析,我们首先基于其假设集的vc维度对AdaBoost进行分析。ADA在T轮增强后AdaBoost选择输出的函数族FT为
FT=sgn(∑t=1Tαtht):αt≥0,ht∈H,t∈[T]
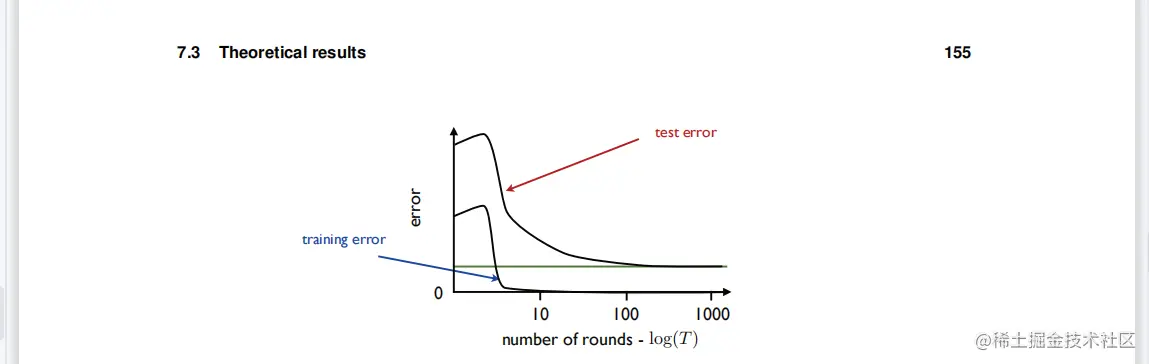
图7.5
使用AdaBoost和(4.5)决策树作为基础学习者的实证结果。在本例中,经过大约5轮增强(T≈5)后,训练误差趋于0,但当T值越大时,测试误差继续减小。FT的vc维数可以根据基本假设H族的vc维数d限定如下(练习7.1):
VCdim(FT)≤2(d+1)(T+1)log29(T+1)e)
上界随着O(dTlogT)的增长而增长,因此,该界表明AdaBoost可能对大的T值过拟合,这确实会发生。然而,在许多情况下,根据经验观察到,AdaBoost的泛化误差随着增强T轮数的函数而减少,如图\mathop 7.5$所示!如何解释这些实证结果?下面的部分提出了一个基于边际的分析,以支持AdaBoost,可以作为这些经验观察的理论解释。
7.3.2
L1几何裕度在第5章中,我们引入了置信裕度的定义,并提出了一系列基于该概念的一般学习边界,该概念特别为支持向量机提供了很强的学习保证。在这里,我们将类似地基于集成方法的置信度概念推导一般学习边界,我们将特别使用它来推导AdaBoost的学习保证。回想一下,一个实值函数f在一个用y标记的点x处的置信度是量yf(x)。对于支持向量机,我们还定义了几何边度的概念,在可分离的情况下,它是具有归一化加权向量w,∥w∥2=1的线性假设置信度的边度的下界。在这里,我们还将为具有范数-1约束的线性假设定义一个几何边度的概念,例如AdaBoost返回的集合假设,并同样将该概念与置信边度的概念联系起来。这也将为我们提供一个机会,以指出在支持向量机中使用的一些概念和术语与在增强中使用的一些概念和术语之间的联系。
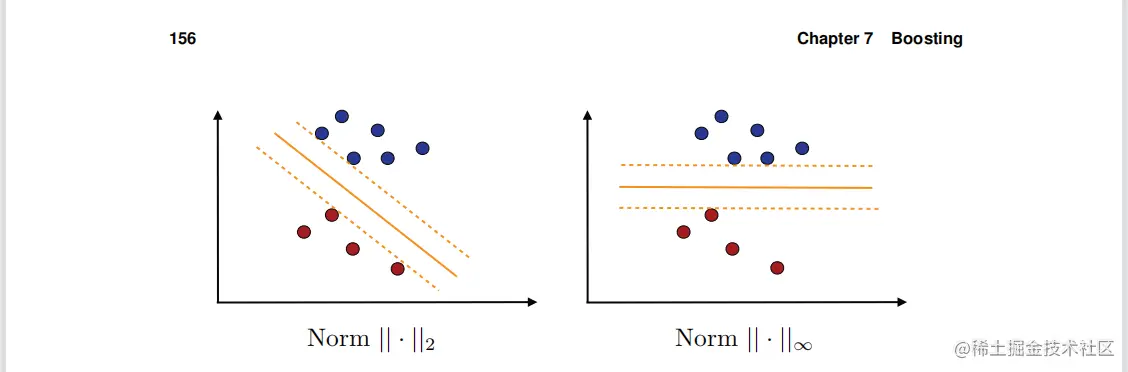
图7.6norm−2和norm−∞的最大边缘超平面。
首先要注意的是一个函数f=∑t=1Tαtht这是碱基假设的线性组合(h1,...,hT)可以等价地表示为一个内积f=a.h,这里α=(α1,...αT)T并且h=(h1,...hT)T。这使得本章中考虑的线性假设与第5章和第6章之间的相似性明显:基本假设值h(x)的向量可以视为与x相关的特征向量,前几章用Φ(x)表示,α是w表示的权重向量。此外,对于如AdaBoost返回的集合线性组合,权值向量是非负的:α≥0。接下来,我们为这种集成函数引入一个几何裕度的概念,它不同于为支持向量机引入的概念,只使用范数1而不是范数2,使用刚刚引入的符号。
定义7.3(L1几何边缘)L1几何边缘ρf(x)的线性函数f=∑t=1Tatht和α=0在某一点x∈X是由
ρf(x)=∥α∥1∣f(x)∣=∥α∥1∣∑t=1Tatht∣=∥α∥1∣α.h(x)∣
f在样本S=上的L1边缘(x1,……,xm)是其在该样本中各点上的最小边缘:
ρf=i∈[m]minρf(xi)=i∈[m]min∥α∥1∣α.h(xi)∣
这个几何边界的定义与SVM算法上下文中给出的定义5.1不同,仅通过权值向量使用的范数:这里的L1范数,定义5.1中的L2范数。为了在下面的讨论中区分它们,让ρ1(x)表示L1ρ2(x)表示第x点处的L2边(定义5.1):
ρ1=∥α∥1∣α.h(x)∣和ρ2=∥α∥2∣α.h(x)∣
7.3理论结果
ρ2(x)是向量h(x)到方程α⋅x=0的超平面的范数2的距离。类似地,ρ1(x)是h(x)到该超平面的范数−∞距离。这个几何差异如图7.6.8所示,我们将用
f−=∑t=1Tαtf=∥α∥1f
由AdaBoost返回的函数f的规范化版本。请注意,如果一个标签为y的点x被正确地分类为f(或者f−),然后是置信度f−)在x处与f的L1几何边缘重合:yf−(x)=∥α∥1yf(x)=ρf(xi).请注意,由于系数αt是非负的,ρf(xi)则是基本假设值ht(x)的凸组合。特别是,如果基本假设ht取[−1,+1]中的值,那么ρf(xi)在[−1,+1]
基于7.3.3边际的分析为了分析AdaBoost的泛化性质,我们首先研究了凸线性系综的辐射器复杂性。对于任何实值函数的假设集H,我们用conv(H)来表示它的凸包,它由
conv(H)={k=1∑pμkhk:p≥1,∀k∈[p],μk≥0,hk∈H,k=1∑pμk≤1. (7.12)
下面的引理表明,值得注意的是,conv(H)的经验辐射器复杂度,通常是一个严格更大的集合,包括H,与H的是一致的。
引理7.4设H是一组从X映射到R的函数。然后,对于任何样本S,我们都有
ℜSconv(H)=ℜSH
一般地说,对于p,q≥1,p和q是共轭物,既是p1+q1=1,∥α∥p∣α.h(x)∣为h(x)到方程α⋅h(x)=0的超平面的范数q距离。
证明:证明来自于一系列简单的等式:
ℜSconv(H)=m1σE[h1,...,hph∈Hsup,μ≥0∥μ∥1≤1i=1∑mσik=1∑pμkhk(xi)]
=m1σE[h1,...,hph∈Hsup,μ≥0∥μ∥1≤1k=1∑pμii=1∑mσkhk(xi)]
=m1σE[h1,...,hph∈Hsup,k∈[p]maxi=1∑mσiσkhk(xi)]
=m1σE[h∈Hsupi=1∑mσkh(xi)]=ℜSH
其中第三个等式遵循对偶范数的定义(见A.1.2节),或观察到p项凸组合的最大化向量μ是将所有权重放在最大项上的值。□
该定理可以直接与定理5.8结合,推导出假设凸组合集合的辐射复杂性推广界。回想一下
Rs,ρ(h)表示带有边际的经验性边际损失ρ
推论7.5(集合雷达采集器边界)
设H表示一组实值函数。修复ρ>0。然后,对于任何一个σ>0,概率至少为1个−σ,以下每个σ都适用于所有的h∈conv(H):
R(h)≤Rs,ρ(h)+ρ2ℜm(H)+2m1ogσ1
R(h)≤Rs,ρ(h)+ρ2ℜm(H)+32m1ogσ2
使用推论3.8和推论3.18根据vc维约束辐射器的复杂性,立即得到以下基于vc维的假设凸组合集合的泛化边界。
推论7.6(集合vc维边界界)设H是一个函数族,取码头+1,−1的vc维数为d。修复ρ>0。然后,对于任何σ>0,概率至少为1−σ,以下情况适用于所有h∈conv(H):
R(h)≤Rs,ρ(h)+ρ2m2dlogdem+2m1ogσ1
这些边界可以推广为所有的ρ∈(0,1]mloglog2σ2,以形式的附加项的价格如定理5.9所述。他们不能是直接应用于AdaBoost返回的函数f,因为它不是基假设的凸组合,但它们可以应用于其归一化版本,f−=∥α∥1∑t=1Tatht∈conv(H)。请注意,从二进制分类的角度来看,f和f−是等价的,因为sgn(f)=sgn(∥α∥1f),因此R(f)=R(∥α∥1f),但他们的经验利润率损失是明显的。
设码头f=∑t=1Tatht表示在样本S上训练后AdABoost返回的分类器的函数。然后,鉴于(7.13),对于任何σ>0,以下概率至少为1−σ:
R(h)≤Rs,ρ(h)+ρ2ℜm(H)+2m1ogσ1
从(7.14)和(7.15)中也可以得到类似的边界。值得注意的是,增强T的轮数并没有出现在泛化界中(7.16)。如果边界损失Rρ(f−),该边界仅取决于基分类器家族的置信度ρ、样本量m和H有效泛化的辐射器复杂度。因此,边界保证了对于相对较大的Rρ很小的有效一代。回想一下,边际损失可以是点x的分数,即∥α∥1y(fx)≤ρ(见(5.38))。根据我们对L1边距的定义,这也可以写如下:
Rs,ρ(f−)≤m∣i∈[m]:yiρf(xi)≤ρ∣(7.17)
此外,下面的定理提供了经验边际损失的界,在后面讨论的条件下,随T减小
定理7.7
设f=∑t=1Tatht表示AdaBoost在T轮增强后返回的函数,并假设所有t∈[T],那ϵt<21,这意味着αt>0。然后,对于任何ρ>0,以下内容如下:
Rs,ρ(f−)≤2T≤t=1∏Tϵt1−ρ(1−ϵ)1+ρ
证明:
使用一般的不等式1μ≤0≤exp(−μ)对所有μ∈R都有效,与7.2一致D−t+1(i)=m∏=1TZteyif(xi),等于Zt=2ϵt(1−ϵt)
定理7.2的证明,以及αt=21log(ϵ1−ϵ)的定义,我们可以写:
m1i=1∑m1yif(xi)−ρ∥α∥1≤0≤0m1i=1∑mexp(−yif(xi)+ρ∥α∥1≤0)
=m1i=1∑meρ∥α∥1[mt=1∏TZt]D−t+1(i)
=eρ∥α∥1t=1∏TZt=eρ∑t′αt
=2Tt=1∏T[ϵ−t1−ϵ−t]ρϵ−t1−ϵ−t
证明就是结论。□
此外,如果所有的T∈[T]我们有γ≤(21−ϵt)且ρ≤2γ,然后表达式4ϵt(1+ρ)是最大的ϵt=21−γ.9因此,上限在经验性的边际损失可以为公式
Rs,ρ(f−)≤[(1−2γ)1+ρ(1−2γ)1+ρ]2T
请注意(1−2γ)1−ρ(1+2γ)1+ρ=(1−4γ2)(1−2γ1+2γ)ρ.这是ρ的一个不断增加的函数,因为我们已经有了(1−2γ1+2γ)>1由于γ>0。因此,如果ρ<γ,它可以是严格的上界如下
(1−2γ)1−ρ(1+2γ)1+ρ<(1−2γ)1−γ(1+2γ)1+γ.
函数γ↦1+ρ<(1−2γ)1−γ(1+2γ)1+γ在区间(0、1/2)上的严格上限为1,因此,如果ρ<γ这时(1−2γ)1−ρ(1+2γ)1+ρ<1而(7.18)的右侧随T的增加而呈指数级下降ρ≫O(1/m)为了给定的边界收敛是必要的,这放置了一个条件γ≫O(1/m)在边缘值上。在实际应用中,基分类器在t轮的误差ϵt可能随着t的函数而增加。非正式地说,这是因为增强迫使弱学习者集中于更难以分类的实例,因为即使是最好的基分类器也不能实现比随机更好的错误。如果ϵt作为t的函数相对较快地接近21,那么定理7.7的界就变得无信息了。
f:ϵ↦log[ϵ1−ρ(1−ϵ1+ρ)]=(1−ρ)logϵ+(1+ρ)log(1−ϵ)的差异,在此区间内,(0,1)是由f′(ϵ)=ϵ1−ρ−1−ϵ1+ρ=2ϵ(1−e)21−2ρ=2ϵ(1−e)(21−2ρ−ϵ)因此,f是一个递增的函数,超过(0,21−2ϵ)这意味着它正在增加,超过(0,21−γ)当γ≥2ρ
之前的分析和讨论表明,如果AdaBoost承认有一个积极的优势(γ≥0),然后ρ<γ,经验性利润率损失Rs,ρ(f−)对于足够大的T,它会变成零(它会以指数速度下降)。因此,AdaBoost在训练样本上实现了γ的l1几何边缘。在第、mathop7.3.5节中,当且仅当训练样本可分离时,边缘γ是正的。在这种情况下,可以选择边缘为在样本上实现的最大L1几何边缘ρmax的一半:γ=2ρmax。因此,对于一个可分离的数据集,AdaBoost可以渐近地实现至少是最大几何边缘的一半的几何边缘,2ρmax.
这种分析可以作为经验观察的理论解释,在某些任务中,即使在训练样本上的误差为零后,泛化误差也随T的函数而减小:当训练样本可分离时,几何裕度继续增加。在(7.16)中,对于T轮后由AdaBoost确定的集合函数f,随着T的增加,ρ可以选择为一个更大的量,使右边的第一项消失(Rs,ρ(f−))而第二项变得更有利,因为它减少了ρ1
但是,AdaBoost是否达到了最大的L1几何边缘ρmax?没有。研究表明,对于一个线性可分离的样本,AdaBoost可以收敛到一个明显小于最大边缘的几何边缘(例如,31而不是83)
7.3.4边际最大化
基于这些结果,已经设计了几种算法的最大化L1几何边际的明确目标。这些算法对应于求解线性程序(LP)的不同方法。根据L1边缘的定义,线性可分离样本S=((x1,y1),...,(xm,ym)的最大边际是由
ρ=αmaxi∈[m]min∥α∥1(yiα.h(xi))
根据最大化的定义,优化问题可以写为:αmaxρ
受以下条件约束:∥α∥1(yiα.h(xi))≥ρ,∀i∈[m]
因为∥α∥1(yiα.h(xi))对α的尺度不变,我们可以限制自己∥α∥1=1进一步寻找非阴性的α,如AdaBoost,会导致以下情况优化:
αmaxρ
服从于yi(α.h(xi))≥ρ,∀i∈[m]
(∑t=1Tα=1)Λ(αt≥0,∀t∈[T])
这是一个线性程序(LP),即一个具有线性目标函数和线性约束的凸优化问题。在实践中,有几种不同的方法来解决相对较大的有限合伙人,使用简单形方法、内点方法,或各种特殊目的的解决方案。
请注意的是,在可分离情况下,该算法的解与定义支持向量机的边际最大化的不同之处仅在于所使用的几何边界(L1vsL2)的定义和权重向量的非负性约束。图7.6说明了在一个简单的情况下使用这两种不同的边界定义发现的边界最大化超平面。左图显示了SVM解,其中距离超平面最近的点相对于范数测量∥.∥2。右边的图显示了L1边缘的解,其中距离超平面最近的点的距离是相对于范数测量的∥.∥∞。
根据定义,刚才描述的LP的解决方案允许一个大于或等于AdaBoost解决方案的L1边距。然而,实证结果并没有显示对LP的解决有系统的好处。事实上,在许多情况下,AdaBoost似乎优于该算法。所描述的边际理论似乎不足以解释这种表现。
7.3.5
在这节中,我们证明AdaBoost允许一个自然的博弈论解释。冯·诺伊曼定理的应用有助于我们将最大边缘和最优边缘联系起来,并阐明AdaBoost的弱学习假设与L1边缘概念的联系。我们首先介绍了一个特定分布的基分类器的边缘的定义。
定义7.8
在训练样本S=((x1,y1),...,(xm,ym)上的分布D的基分类器是由ht的边缘
γt(D)=21−ϵt=21i=1∑myiht(xi)D(i)
AdaBoost的弱学习条件现在可以表述如下:存在γ>0,因此对于训练样本上的任何分布D和任何基础
表7.1标准石剪刀布游戏的损失矩阵
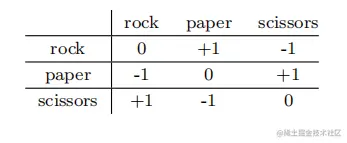
分类器ht,适用于如下:γt(D)≥γ
分析定理7.2和系数αt的非负性都需要这个条件。我们将把提升作为一个两人零和游戏。定义7.9(零和博弈)一个有限的两人零和博弈由一个损失矩阵M∈Rm×n组成,其中M是行玩家可能的行动(或纯策略)的数量,n是列玩家可能的行动的数量。条目Mij是当行播放者采取行动i和列播放者采取行动j时的损失(或相当于列支付者的回报)。表7.1显示了一个熟悉的“石头剪刀布”游戏的损失矩阵的例子。定义7.10(混合策略)行播放器的混合策略是在m个可能的行操作上的分布ρ;列播放器的混合策略是在n个可能的列操作上的分布q。对于混合策略ρ和q,行玩家的预期损失(列玩家的预期收益)是i pE[Mij]=i=1∑mj=1∑npiMijqj=PTMq
以下是第8章所证明的博弈论的一个基本结果。定理7.11(Von诺伊曼极大极小定理)对于由矩阵M定义的任意有限的二人零和对策,以下等式成立:
PminqmaxPTMq=qmaxPminPTMq
(7.22)中的共同值称为游戏的值。该定理指出,对于任何两人零和博弈,每个玩家都存在一个混合策略,为了与其他章节讨论的结果一致,我们考虑损失矩阵而不是回报矩阵(它的相反)这样一个的预期损失与另一个的预期损失收益相同,两者都等于游戏的价值。注意,给定行玩家的策略,列玩家可以选择一个纯粹的策略来优化他们的回报。也就是说,列播放器可以选择对应于向量PTM的最大坐标的单个策略。类似的评论也适用于相反的评论。因此,极大极小定理的另一种等价形式是
Pminj∈[n]maxPTMej=qmaxi∈[m]mineiTMq
其中ei表示第个单位向量。我们现在可以把AdaBoost看作是一个零和游戏,其中行玩家的动作是选择一个训练实例xi,i∈[m],而列玩家的动作是选择一个基础学习者ht,t∈[T]。因此,行玩家的混合策略是在训练点指数上的分布D。列播放器的混合策略是基于分类器索引的分布[T]。这可以从一个非负向量α≥0中定义:分配的权重t∈[T]是αt/∥α∥1。AdaBoost的损失矩阵M∈(−1,1)m×T由Mit=yiht(xi)定义为所有(i,t) ∈[m]×[T]。根据冯·诺伊曼定理(7.23),以下观点成立:
D∈Dmin[t∈[T]]max∑i=1mD(i)yiht(xi)=α≥0maxi∈[m]minT=1∑t∥α∥1αtyiht(xi)(7.24)
其中,D表示在训练样本上的所有分布的集合。设ρα(x)表示由所定义的分类器的点x的边缘f=∑t=1Tαtht。结果可以根据边缘和边缘重写如下:
2γ∗=2Dmin [t∈[T]]maxγt(D)=αmaxi∈[m]minρα(xi)=ρ∗,(7.25)
其中ρ∗是一个分类器的最大边缘,γ∗是可能的最佳边缘。这个结果有几个意义。首先,它表明,弱学习条件γ∗意味着ρ∗>0,因此存在一个具有正边际的分类器,这激发了对非零边际的搜索。AdaBoost可以被看作是一种寻求实现如此非零边际的算法,尽管,正如前面所述,AdaBoost并不总是实现最优边际,因此在这方面是次最优的。此外,我们还看到,“弱学习”假设最初似乎是算法所需要的最弱条件(性能优于随机),实际上是一个强条件:它意味着训练样本与边际2γ∗>0是线性可分离的。线性可分离性通常不适用于实践中发现的数据集。
7.4L1-正则化在实践中
训练样本可能不能线性分离,AdaBoost可能不承认正边,在这种情况下,弱学习条件不成立。也可能是AdaBoost确实承认了一个积极的优势,但γ非常小。在这种情况下,运行AdaBoost可能会导致某些基分类器hj产生较大的总混合权值。这可能是因为该算法越来越专注于一些难以分类的例子,而且其权重也在不断增长。只有少数基本分类器可以获得最佳的性能,算法不断选择它们,从而增加它们的总混合权重。这些具有总混合权重相对较大的基分类器最终在集合f中占主导地位,因此只决定了分类决策。结果集成的性能通常很差,因为它几乎完全取决于一些基本分类器的性能。有几种方法可以避免这种情况。一种是限制增强T的轮数,这也被称为提前停止。另一个是控制混合物重量的大小α−=(α−1,...,α−N)∈RN通过
G(α−)=m1i=1∑meyif(xi)+λ∥α∥1=m1i=1∑meyij=1∑Nα−jhj(xi)+λ∥α∥1,(7.26)
其中,对于AdaBoost,f是一个由f=α−jhj,使用α−≥0。目标函数G是α−的一个凸函数,作为AdaBoost的凸目标和α−的范数−1的和。L1正则化的AdaBoost包括将坐标下降应用到目标函数G。我们现在表明,该算法可以从推论7.5或推论7.6的集成方法的基于边际的保证中直接导出。因此,这样L1正则化的AdaBoost比AdaBoost受益于更有利和更自然的理论保证。通过将推论7.5推广到ρ上的均匀收敛界,对于任何σ>0,概率至少为1−σ,以下适用于f=∑j=1Nα−jhj与∥α∥1≤1和所有ρ∈的所有集成函数(0,1]:
R(f)≤m1i=1∑m1f(xi)≤ρ+ρ2ℜm(H)+mloglog2ρ2+2mlog2σ2.(7.27)
这个不等式对于ρ>1也很简单地适用,因为在这种情况下,界的右边的第一项等于1。事实上,在这种情况下,通过H¨老的不等式,对于任何x∈X,我们有f(x)=j=1∑nα−jhj(xi)≤∥α∥1maxj∈[N]∣hj(xi)∣≤∥α∥1≤1≤ρ
现在,鉴于一般的上界1u≤0≤e−u适用于所有u∈R,概率至少为1−σ,以下适用于所有f(x)=j=1∑nα−jhj(xi)与∥α∥1≤1和所有ρ>0:
R(f)≤m1i=1∑me1−ρf(xi)+ρ2ℜm(H)++mloglog2ρ2+2mlog2σ2.(7.28)
由于对于任何ρ>0,f/ρ承认与f相同的泛化误差,概率至少为1−ρ,所有具有∥α∥1≤1和/ρ的f(x)=j=1∑nα−jhj(xi)不等
R(f)≤m1i=1∑me1−f(xi)+ρ2ℜm(H)++mloglog2ρ2+2mlog2σ2.(7.29)
这个不等式可以用来推导出一个选择α−和ρ>0来最小化右侧的算法。关于ρ>0的最小化不会导致凸优化,而是依赖于影响第二项和第三项的理论常数因素,这可能不是最优的。因此,ρ>0被作为算法的自由参数,通常通过交叉验证来确定。现在,由于只有右边的第一项依赖于α−,所以边界建议选择α−作为以下优化问题的解:
∥α∥1≤ρ1minm1i=1∑me−f(xi)=m1i=1∑me−j=1∑nα−jhj(xi)
引入拉格朗日变量λ≥0,优化问题可以等价地写为
∥α∥1≤ρ1minm1i=1∑me−j=1∑nα−jhj(xi)+λ∥α∥1
由于在(7.30)约束下的任何ρ选择,公式(7.31)中存在一个等价的双变量λ,达到相同的最优α−,因此可以通过交叉验证自由选择λ≥0。因此,所得到的目标函数与L1正则化的AdaBoost的目标函数完全一致。
AdaBoost有几个优点:它简单,实现简单,每一轮提升的时间复杂性作为样本量的函数是相当有利的。如前所述,当使用决策树桩时,每一轮提升的时间复杂度为O(mN)。当然,如果特征空间N的维数非常大,那么算法实际上可能会变得相当慢。AdaBoost还受益于丰富的理论分析。然而,该算法仍存在许多相关的理论问题。例如,正如我们所看到的,该算法实际上并没有最大化边际,但是能够最大化边际的算法并不总是优于它。这表明,也许一个基于不同于最小边际的概念的更好的分析,可以更多地阐明算法的特性。
该算法的一个小缺点是需要选择参数T和基分类器集。选择提高T(停止准则)的轮数对算法的性能至关重要。VC维数分析表明,T值越大,会导致过拟合。在实践中,T通常是通过交叉验证来确定的。基分类器的选择也至关重要。基分类器H族的复杂性出现在所给出的所有边界中,为了保证泛化,控制它是很重要的。另一方面,不够复杂的假设集可能导致低边际。
AdaBoost最严重的缺点可能是它在噪声时的性能,至少在某些任务中是这样。由于算法的性质,分配给难以分类的例子的分布权重随着增强轮数的增加而大幅增加。这些示例可能最终会主导基分类器的选择,而基分类器有足够多的轮,将在AdaBoost定义的线性组合的定义中发挥不利作用。已经提出了几种解决方案来解决这些问题。一种是使用比AdaBoost的指数函数“较低攻击性”的目标函数,如逻辑损失,来惩罚较少分类不正确的点。另一个解决方案是基于正则化的,例如,前一节中描述的L1正则化的AdaBoost。
对AdaBoost的实证研究表明,均匀噪声严重损害了其精度。最近的理论结果也证实了这一点,表明基于凸势的增强算法甚至不能容忍低水平的随机噪声。此外,即使使用L1正则化或早期停止,这些问题也被证明仍然存在。然而,在这些实验或分析中使用的统一噪声模型是相当不现实的,似乎不太可能在实践中出现第7章的增强。该模型假设具有某种固定概率的标签损坏会均匀地影响所有实例。显然,在存在这些噪声的情况下,任何算法的性能都会下降。然而,实证结果表明,对于该均匀噪声模型,AdaBoost的性能比其他算法下降。最后,请注意,AdaBoost在噪声存在下的行为实际上可以用作检测异常值的有用特性,也就是说,标记错误或难以分类的例子。经过一定数量的增强后具有大权重的例子可以被识别为异常值。
7.6章节指出
弱学习算法是否可以增强来获得强学习算法的问题首先是由卡恩斯和安定特[1988,1994]提出的,他也对分布依赖的设置给出了这一结果的否定证明。在与分布无关的情况下,这一结果的第一个积极证明是由夏皮尔[1990],后来又由弗罗恩德[1990]提供的。这些早期的增强算法,通过过滤增强[夏皮尔,1990]或由大多数增强[Freund,1990,1995]是不实际的。由弗罗恩德和夏皮尔[1997]引入的AdaBoost算法解决了其中的几个实际问题。Freund和Schapire[1997]进一步对算法进行了详细的介绍和分析,包括其经验误差界、vc维分析及其在多类分类和回归中的应用。
AdaBoost的早期实验由德鲁克、夏皮尔和西马德[1993]进行,他们首次实现了基于神经网络的弱学习者和科尔特斯[1995],他们报告了AdABoost结合决策树的经验表现,特别是决策树桩。
AdaBoost与应用于指数目标函数的坐标下降相一致的事实后来被Duffy和Helmbold[1999],Mason等人证明。以及弗里德曼和2000年。弗里德曼、哈斯蒂和蒂布希拉尼[2000]也用加性模型给出了增强的解释。他们还指出了AdaBoost和逻辑回归之间的密切联系,特别是它们的目标函数在零附近有相似的行为,或者他们的期望允许相同的最小化器,并导出了一种基于逻辑损失的替代增强算法LogitBoost。Lafferty[1999]展示了如何从布雷格曼发散中导出一个增量算法家族,包括LogitBoost,并被设计为在改变一个参数时非常近似于AdaBoost。基维宁和Warmuth[1999]给出了AdaBoost作为熵投影的等价观点。他们表明,样本分布发现7.6章注意在每一轮大约是解决方案的问题找到最近的分布在前一轮,受约束,正交的误差向量的基础假设。在这里,接近度是用布雷格曼散度来测量的,对于AdaBoost,它是非归一化的相对熵。柯林斯、夏皮尔和Singer[2002]后来证明,增强和逻辑回归是基于布雷格曼分歧的共同框架的特殊实例,并利用它给出了AdaBoost的第一个收敛证明。黎巴嫩和拉弗蒂[2001]给出了AdaBoost和逻辑回归之间的另一个直接关系,他们表明这两种算法在相同的特征约束下最小化相同的扩展相对熵目标函数,除了逻辑回归的附加归一化约束。
定理7.7
夏皮尔、弗罗恩德、巴特利特和李[1997]首次提出了对AdaBoost的基于边际的分析,它给出了经验边际损失的一个界。我们的演示是基于科尔钦斯基和潘琴科[2002]使用拉德马赫复杂性的概念对边缘边界的优雅推导。Rudin等人。[2004]给出了一个例子,表明,一般来说,AdaBoost并不能最大化l1边际。R¨atsch和Warmuth[2002]提供了AdaBoost在某些条件下实现的边际的渐近下界。基于LP的L1边际最大化是由于Gro夫和舒尔曼[1998]。R¨atsch,Onoda和M¨uller[2001]建议使用软边缘来修改该算法,并指出了它与支持向量机的联系。弗罗恩德和夏皮尔[1996,1999b]指出了极大极大定理的配子理的解释和应用[冯·诺伊曼,1928];参见格罗夫和舒尔曼[1998]和布雷曼[1999]。
7.Ratsch、Mika和AdaBoost算法Ratsch和[2001]提出并进行了分析。Cortes、Mohri和Syed[2014]引入了一种新的增强算法深推进器,他们证明该算法受益于更好的学习保证,即使作为基础分类器集相对丰富的家族,也包括有利的保证,例如非常深的决策树家族,或其他类似复杂的家族。在深推进器中,每次迭代中决定将哪个分类器添加到集成以及分配哪个权重取决于分类器所属子族的(数据依赖)复杂性。Cortes、Mohri和Syed[2014]进一步表明,经验上的深推进器比AdaBoost、逻辑回归和L1正则化变体取得了更好的性能。AdaBoost和L1规则化的AdaBoost都可以看作是深推进器的特殊实例。
迪特里奇[2000]为均匀噪声会严重损害AdaBoost的准确性提供了广泛的经验证据。这已经被170章报道,促进了其他一些作者。Long和Servedio[2010]最近进一步表明,基于凸势的增强算法无法容忍随机噪声,即使是L1正则化或早期停止。有几个优秀的调查和教程与促进有关[夏皮尔,2003年,梅尔和R¨atsch,2002年,梅皮尔和R¨atsch,2003年],包括最近的书夏皮尔和弗雷恩德[2012]完全致力于这一主题,有大量的参考文献列表和详细的介绍。
7.7练习
7.1AdaBoost假设集的vc维度。证明了经过T轮助推后,AdaBoost的假设集FT的vc维数的上界,如方程(7.9)所述。
7.2替代的目标函数。
这个问题研究了用不同于AdaBoost的目标函数定义的增强类型算法。我们假设训练数据作为m个标记的例子给出(x1,y1),...,(xm,ym)∈X×−1,+1.。我们进一步假设Φ是R上严格增加的凸可微函数,这样:∀x≥0,Φ(x)≥1和∀x>0,Φ(x)>0.
(a)考虑损失函数L(a)=i=1∑mΦ(−yif(xi))其中f是基分类器的线性组合,即f=∑t=1Tatht(如AdaBoost)。利用目标函数L导出一种新的增强算法,特别描述了使用坐标下降在每一轮提升时选择的最佳基分类器。
(b)考虑以下函数:(1)零损失Φ1(−u)=1u≤0;(2)最小平方损失Φ1(−u)=(1−u)2;(3)SVM丢失Φ1(−u)=max(0,1−u);和(4)逻辑损失Φ1(−u)=log(1+e−u);。哪些函数满足本问题中前面所述的对Φ的假设?
(c)对于每个满足这些假设的损失函数,推导出相应的增强算法。该算法(s)与AdaBoost有何不同?
7.3更新保证
假设AdaBoost的主要弱学习者假设成立。让我们成为第t轮中选择的基础学习者。表明在第、mathopt+1轮中选择的基础学习者ht+1必须与ht不同
7.4加权实例
让训练样本为S=((x1,y1),...,(xm,ym)假设我们希望惩罚在xi和xj上所犯的不同错误。为此,我们将一些非负重要性权重与每个点xi关联起来,目标函数F(α)=∑i=1mwie−yif(xi),其中f=∑t=1Tatht。证明该函数是凸的和可微的,并使用它推导出一个引导类型算法。
7.5
将两个向量x和x′的非归一化相关性定义为这些向量之间的内积。证明由AdaBoost定义的分布向量(Dt+1(1),…,Dt+1(m))和分量yiht(xi)的向量是不相关的。
7.6
修复ϵ∈(0,1/2)。让训练样本为平面上的4m点定义,4m负点在坐标(1,1),另一个4m负点在坐标(1,1),4m(1−ϵ)正的点都在坐标上(1,1),和4m(1−ϵ) 个正点均在坐标上,和4m(1−ϵ) 个正点均在坐标上(1,1)。描述在此示例上运行AdaBoost时的行为。T轮后算法返回什么解决方案?。描述在此示例上运行AdaBoost时的行为。T轮后算法返回什么解决方案?
7.7
耐噪音的AdaBoost。AdaBoost在存在噪声的情况下可能明显过拟合,部分原因是对错误分类的例子的高度惩罚。为了减少这种影响,我们可以使用以下目标函数:
F=i=1∑mG(−yif(xi)),(7.32)
其中G是在R上定义的函数
G(x)={exx≤0x+1x>0
(a)表明函数G是凸的和可微的。(b)利用F和贪婪坐标下降推导出一种类似于AdaBoost的算法。(c)比较该算法与AdaBoost的经验错误率的降低。7.8简化的广告提升。假设我们通过将参数αt设置为固定值αt=α>0来简化AdaBoost,独立于提升轮t.(a)让γ为(21−ϵt)≥γ>0。通过分析经验误差,找到α作为γ函数的最佳值。(b)对于的这个值,该算法是否在每一轮中为正确分类和错误分类的例子分配相同的概率质量?如果没有,哪个集合被分配了一个更高的概率质量?
AdaBoost(M,tmax)
λ1,j←0 for i=1
for t ← 1 to tmax do
dt,i←∑k=1mexp(−(Mλt)i)exp(−(Mλt)i)fori=1,...,m
jt←argmaxj(dtTM)jt
rt←argmaxj(dtTM)jt
αt←21log(1−rt1+rt)
λt+1←λt+αtejt,其中ejt的位置jt为1,其他位置为0
return∥λtmax∥1λtmax
AdaBoost根据矩阵M定义,该矩阵编码每个训练点上每个弱分类器的准确性。
(c)使用α的值,给界算法的经验误差只取决于γ和轮的促进T
(d)使用之前的界限,表明T>日志2γ2logm,结果假设与大小的样本一致。
(e)让s使用的基础学习者的vc维度。给出了T=[2γ2logm]+1后得到的一致假设的推广误差的一个几轮的提升。(提示:使用函数族的vc维数这个事实sgn(∑t=1Tαtht):αt∈R以2(s+1)Tlog2(eT))为界。现在假设γ随m而变化。根据推导出的边界,如果γ(m)=O(mlogm)?)
7.9AdaBoost示例
在本练习中,我们考虑一个由8个训练点和8个弱分类器组成的具体示例。
(a)定义一个m×n矩阵M,其中Mij=yihj(xi),i.e..如果训练例子i被弱分类器hj正确分类,则为Mij=+1,则为−1。设dt、λt∈Rn、∥dt∥1=1和dt,i(分别为λt、i)等于dt的第i个分量(分别为λt)。现在,考虑如图7.7,并将M定义为如下,包括8个训练点和8个弱分类器。
M=⎩⎨⎧−1,1,1,1,1,−1,−1,1−1,1,1,−1,−1,1,1,11,−1,1,1,1,−1,1,11,−1,1,1,−1,1,1,11,−1,1,−1,1,1,1,−11,1,−1,1,1,1,1,−11,1,−1,1,1,1,−1,1−1,1,1,1,−1,−1,1,−1
假设我们从数据点上的以下初始分布开始:
d1=(83−5),83−5,61,61,61,85−185−1,0)T
使用M、d1和tmax=7计算AdaBoost算法的前几步。在每一轮的提升中都选择了哪些弱分类器?你注意到有什么模式吗?
(b)AdaBoost为这个例子产生的L1标准边际是多少?
(c)与其使用AdaBoost,想象一下我们使用以下系数组合我们的分类器:[2,3,4,1,2,2,1,1]×161在这种情况下的保证金是多少?AdaBoost能使利润率最大化吗?
7.10在未知标签下提升
考虑以下分类问题的变体,除了正和负标签+1和−1外,点还可以标记为0。这可能对应于一个点的真实标签未知的情况,一种在实践中经常出现的情况,或者更普遍的是学习算法对预测该点的−1或+1没有损失的事实。设X为输入空间,设Y=−1,0,+1。在标准的二进制分类中,一对(x,y)∈上f:X×Y的损失是由1yf(x)<0定义的。
考虑一个样本S=((x1,y1),...,(xm,ym)∈(X×Y)2以及取−1,0,+1中值的基函数的假设集H。对于基本假设ht∈H和指数∈的分布,定义s∈−1,0,+1的ϵts,ϵts=Ei D[1yiht(xi)=s]
(a)使用与AdaBoost相同的目标函数,根据ϵtss导出该设置的增强式算法。您应该仔细证明算法的定义。
(b)在这种情况下,弱学习的假设是什么?
(c)编写该算法的完整伪代码。
(d)给出了该算法的训练误差的一个上界,作为增强轮数和ϵtss的函数。
7.11
如本章所述,AdaBoost可以看作是应用于指数目标函数的坐标下降。在这里,我们考虑了另一种集成方法算法,HingeBoost,它包括将坐标下降应用到一个基于铰链损失的目标函数。考虑为所有α∈RN定义的函数
F(α)=∑i=1mmax(0,1−yij=1∑nαjhj(xi)),(7.34)
其中hj是属于假设集H的基分类器,取值为−1或+1的基分类器。
(a)表明F是凸的,并且允许一个沿任意方向的左右导数。
(b)对于任意j∈[N],设ej表示基假设hj对应的方向。设αt表示坐标下降的t≥0迭代后得到的系数αt,j、j∈[N]的向量,ft=j=1∑n=αt,j,jh,j表示t迭代后得到的预测器。用t−1迭代右导数后F′+(αt−1,ej)和左导数F′−(αt−1,ej)的表达式。
(c)对于任意j∈[N],在αt−1处定义最大方向导数σF(αt−1,ej)如下:
σF(αt−1,ej)=⎩⎨⎧0ifF−(′αt−1,ej)≤0≤F+(′αt−1,ej)F+(′αt−1,ej)ifF−(′αt−1,ej)≤F+(′αt−1,ej)F−(′αt−1,ej)≤F(′αt−1,ej)≤F+(′αt−1,ej)
这里考虑的坐标下降所考虑的方向ej是最大化∣σF(αt−1,ej)∣。一旦选择了最佳方向j,就可以通过使用网格搜索来最小化F(αt−1+ηej)来确定步骤η。给出手指Boost的伪代码。
7.12实证边际损失增加
如本章所述,AdaBoost可以看作是应用于经验误差的凸上界的坐标下降。在这里,我们考虑一种寻求最小化经验边际损失的算法。对于任何0≤ρ<1让Rs,ρ(f)=m1∑i=1m1yif(xi)≤ρ表示f=∑t=1Tαt∑t=1Tαtht形式的函数f对于标记的样本的经验边际损失S=(x1,y1),...,(xm,ym),
(a)显示Rs,ρ(f)≤m1i=1∑mexp(−yit=1∑Tαtht(xi)+ρt=1∑Tαt)的上界如下:
(b)对于任何ρ>0,让Gρ为所有α≥0定义的目标函数
Gρ(α)=m1i=1∑mexp(−yit=1∑Tαtht(xi)+ρt=1∑Tαt)
使用hj∈H表示所有j∈[N],以及在课堂上使用的符号。表明Gρ是凸的和可微的。
(c)通过应用(最大)坐标下降到Gρ,得到一个提升式的算法Aρ。您应该详细证明算法的推导,特别是在每一轮和步骤中选择的基分类器的选择。并与AdaBoost中的同类产品进行了比较。
(e)给出了算法Aρ的完整伪代码。你能说些什么关于A0算法呢?
(f)提供一个绑定Rs,ρ(f).
i.证明上界Rs,ρ(f)≤exp(∑t=1αtρT,其中归一化因子Zt被定义为AdaBoost的情况(αt是Aρ在第t轮选择的步骤)。
ii.给出Zt作为ρ和ϵt的函数,其中ϵt是Aρ在t轮发现的假设的加权误差(定义与第7章类中的助推相同)。使用它来证明以下上界
Rs,ρ(f)≤(u21+ρ+u21−ρ)Tt=1ΠT ϵ1−ρ(1−ϵ)1+ρ.其中u=1+ρ1−ρ。
iii.假设对于所有的t∈[T],21−ρ上一个问题显示−ϵt>γ>0。使用的结果
Rs,ρ(f)≤exp(−1−ρ22γ2T)
(提示:无需使用以下身份:
(u21+ρ+u21−ρ) ϵ1−ρ(1−ϵ)1+ρ≤1−21−ρ2(21−ρ−ϵ)2.
适用于21−ρ−ϵt>0)显示,对于T≥22γ2(logm)(1−ρ2),训练数据的所有点至少有ρ。
以轴对齐的超平面作为基础分类器的AdaBoost示例。()最上面的一行显示了每一轮推进时的决策边界。下面一行显示了每一轮如何更新权重,给出错误(正确)权重增加(减少)。()最终分类器的可视化,构造为基分类器的非负线性组合。
在基分类器是从映射到{}的函数时,AdaBoost的伪代码,因此{}。
该算法以一个标记的样本))作为输入,其中,() 为所有的,并在索引{,…,}上保持一个分布。最初(第至行),分布是均匀的()。在每一轮增强时,即循环的每次迭代,选择一个新的基分类器,使由分布加权的训练样本的误差最小化: