简单聊一聊—线性判别分析(LDA)

zidea
1,163 阅读2分钟

小知识，大挑战！本文正在参与“程序员必备小知识”创作活动。

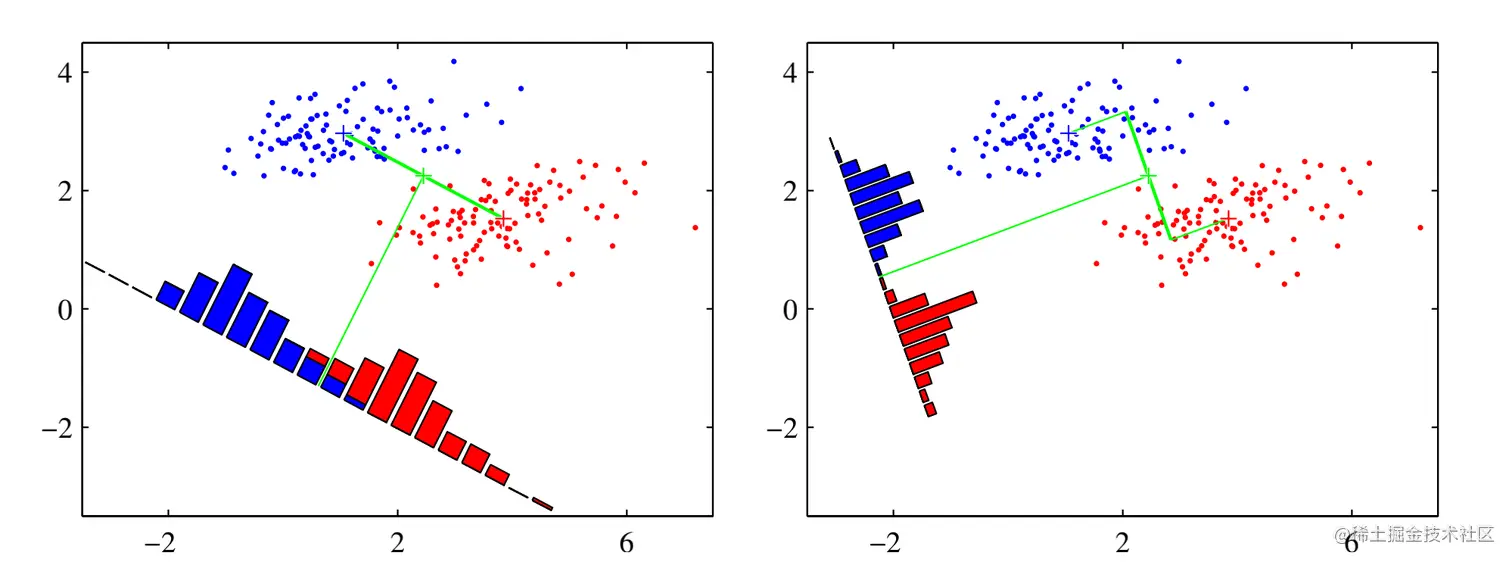
LDA(Linear Discriminant Analysis) 与之间介绍的 PCA 非常相似、一种经典的有监督数据降维方法。LDA 的主要思想是将一个高维空间中的数据投影到一个较低维的空间中，且投影后要保证各个类别的类内方差小而类间均值差别大，这意味着同一类的高维数据投影到低维空间后相同类别的聚在一起，而不同类别之间相距较远。

向量在某一向量上投影

如何想要计算 xx 在 uu 方向投影的长度可以这样计算。

cos⁡θ=x⋅u∣∣x∣∣∣∣u∣∣ xcos⁡θ=x⋅u\begin{aligned} \cos \theta = \frac{x\cdot u}{||x||||u||}\ x \cos \theta = x \cdot u \end{aligned}

通常将 uu 长度考虑为 1 这样我们就得到上面的公式。

y=wTxy =w^Tx

现在的 xix^i 是有标签，希望在某一个方向投影后，这些不同类别点之间距离最大，也可以理解不同类别的平均数间距离越大越好，这样这些类别就容易分开。

m1=1N1∑n∈C1xn,,m2=1N2∑n∈C2m_1 = \frac{1}{N_1} \sum_{n \in C_1} x^n ,, m_2 = \frac{1}{N_2} \sum_{n \in C_2}
m2−m1=wT(m2−m1)m_2 - m_1 = w^T(m_2 - m_1)

通常还需要加入一个约束条件 wTw=1w^Tw = 1,然后解这个问题。

wT(m2−m1)+λ(wTw−1)w^T(m_2 - m_1) + \lambda(w^Tw - 1)
∂L(w)∂w=(m2−m1)+λw=0\frac{\partial L(w)}{\partial w} = (m_2 - m_1) + \lambda w = 0

从而得到下面式子，也就是 ww 与 m2−m1m_2 - m_1 成正比

w∝(m2−m1)w \propto (m_2 - m_1)

lda_001.png

J(w)=(m2−m1)2s12+s22J(w) = \frac{(m_2 - m_1)^2}{s_1^2 + s_2^2}
  • 类别间的均值距离最大
  • 每个类别内方差最大
sk2=∑i∈Ck(yi−mk)2s_k^2 = \sum_{i \in C_k} (y^i - m_k)^2
J(w)=wTSBwwTSWw SB=(m2−m1)(m2−m1)T SW=∑i∈C1(xi−m1)T(xi−m1)+∑i∈C2(xi−m2)T(xi−m2)\begin{aligned} J(w) = \frac{w^TS_Bw}{w^TS_Ww}\ S_B = (m_2 - m_1)(m_2 - m_1)^T\ S_W = \sum_{i \in C_1}(x^i - m_1)^T(x^i - m_1) + \sum_{i \in C_2}(x^i - m_2)^T(x^i - m_2) \end{aligned}

接下来就是 J(w)J(w) 对 ww 进行微分,这里分母部分是大于等于 0 因为我们关心的分子部分，分子部分的一阶导函数是等于 0 。

2SBw(wTSWw)−2(wTSBw)SWw=0 SBw(wTSWw)=(wTSBw)SWw\begin{aligned} 2S_Bw(w^TS_Ww) - 2(w^TS_Bw)S_Ww = 0\ S_Bw(w^TS_Ww) = (w^TS_Bw)S_Ww \end{aligned}
  • 分子微分乘以分母减去分母乘以分子的微分
  • wTSWww^TS_Ww 和 wTSBww^TS_Bw 都是标量
SB=(m2−m1)(m2−m1)T SBw=(m2−m1)(m2−m1)Tw\begin{aligned} S_B = (m_2 - m_1)(m_2 - m_1)^T\ S_B w = (m_2 - m_1)(m_2 - m_1)^Tw \end{aligned}

(m2−m1)Tw(m_2 - m_1)^Tw 是一个标量所以 SBwS_Bw 与m2−m1m_2 - m_1

w∝SW−1(m2−m1)w \propto S_W^{-1}(m_2 - m_1)

所以 LDA 并不是判别器，而是数据处理过程，找到一个投影方式

总结

输入数据为 D=(x1,y1),(x2,y2),⋯ ,(xN,yN)D= {(x^1,y^1),(x^2,y^2),\cdots,(x^N,y^N)} 数据为 N 个样本，其中每一个样本为 mm 维的特征的样本，y∈C1,C2,⋯ ,CKy \in {C_1,C_2,\cdots,C_K } 也就是说 yy 的样本类别可能维 KK

  • 标准化数据，计算每一个类别的均值和方差
  • 计算类内散度矩阵 SBS_B
  • 计算类间散度矩阵 SWS_W
  • 将 SBS_B 和 SWS_W 代入上面公式计算得到特征值 λ\lambda 和特征向量 WW，取前面几个最大的特征值向量λ'与特征向量相乘得到降维转换矩阵 λ′W\lambda^{\prime}W
  • 将原来的数据与转换矩阵相乘得到降维后的数据 (λ′W)TX(\lambda^{\prime}W)^TX
avatar
文章
阅读
粉丝