机器学习笔记——线性模型

linear model 线性模型 基本形式

给定由$d$个特征描述的实例$\pmb{x}=(x_1;x_2,...,x_d)$，其中$x_i$是$\pmb{x}$中的第$i$个特征，线性模型的目标在于通过特征的线性组合来构成预测函数：

通过学习权重$\pmb{x}$和参数$b$就能够确定一个预测模型。

线性模型的优点在于：

• 可以通过引入层级结构或高维映射来表示非线性模型
• 权重的引入直观表示了不同特征的重要程度，因此模型有很好的可解释性（comprehensibility）。

linear regression 线性回归

给定数据集$D=\{(\pmb{x}_1,y_1),...,(\pmb{x}_m,y_m)\}$，其中$\pmb{x}_1=(x_{i1};...;x_{id}),y_i \in \mathbb{R}$。考虑最简单的情况即特征只有一个$D=\{(x_i,y_i)\}^m_{i=1},x_i \in \mathbb{R}$。对于离散的特征，不同特征值间存在序列（order）关系，可以通过连续化将其转化为连续的数值，如二分类可以转化为(0, 1)，三分类转化为(0, 0.5, 1)。对于特征值间不存在序列关系的情况，假定有$k$个特征值则一般会转化为$k$维向量，如瓜类取值西瓜、南瓜、黄瓜，则使用(0, 0, 1)、(0, 1, 0)和(1, 0, 0)来表示。

线性回归的学习函数为：

为了确定$w$和$b$的值，使用均方误差最小化方法来求解两个参数：

均方误差方法实际上对应于欧氏距离（Euclidean distance），基于均方误差最小化求解模型的方法称为最小二乘法（least square method）。在线性回归中，最下二乘法目标在于找到一条直线使得所有样本点到直线的欧氏距离之和最小。

通过令$E_{(w,b)}=\sum^m_{i=1}(y_i,-wx_i-b)^2$最小化来求解$w,b$的过程称为线性回归模型的最小二乘参数估计（(parameter estimation），对$E_{(w,b)}$分别求$w,b$的偏导得到：

令上面两式都为0，得到$w,b$的最优解的闭式（closed-form）解 （$E_{(w,b)}$是关于$w$和$b$的凸函数，因此可以求导得到参数的最优解）：

扩展到多个特征的情况，即多元线性回归（(multivariate linear regression）。

多元线性回归中的特征值不再是一个标量而是一个向量，同样参数$w$也应是一个向量，将$\pmb{w},b$表示为向量形式$\hat{\pmb{w}}=(\pmb{w};b)$，数据集D表示为一个$m \times (d+1)$大小的矩阵$\pmb{X}$，每行对应一个样本，每行的前$d$个元素为样本的$d$个特征值，最后的元素恒为1（加这一项的目的是去掉上面式子中的$+b$，$\hat{\pmb{y}}$可以直接用$\pmb{X}\hat{\pmb{w}}$表示），即：

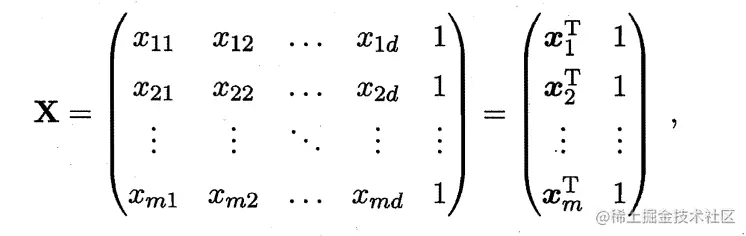
标记也用向量表示：$\pmb{y}=(y_1,y_2,...,y_m)$，得到最小化均方误差的表达式：

此处实质上是求$\pmb{y}-\pmb{X}\hat{\pmb{w}}$的欧几里得范数（L2范数），它表示两点间的距离（向量的模长）。

对$\hat{w}$求导得到：

令上式为0即可得到$\hat{w}$的最优解。

令$\pmb{X}^T\pmb{X}$为满秩矩阵或正定矩阵解上式可得：

令$\hat{\pmb{x}}_i=(\pmb{x}_i,1)$最终学得的多元线性回归模型为：

而当$\pmb{X}^T\pmb{X}$不是满秩矩阵时（现实任务中可能出现样本包含大量的特征导致其特征数大于样本数的情况），这种情况下会解出多个$\hat{w}$，此时就需要用到学习算法的归纳偏好来决定选择哪个$\hat{w}$，一个常用做法是引入正则化项（regularization）。

线性回归模型可简写为：

实际上这个式子也能用于逼近$y$的衍生物，如$\ln y=\pmb{w}^T\pmb{x}+b$，这称为对数线性回归。形式上是线性回归是，实际上已经转换为了求输入空间到输出空间的非线性函数映射，如下图所示：

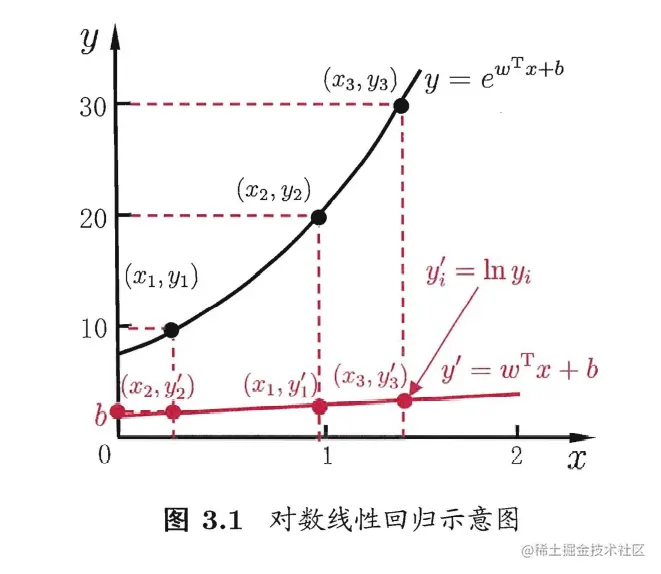
因此考虑引入单调可微函数$g(\cdot)$，令： $y=g^{-1}(\pmb{w}^T\pmb{x}+b)$，这个模型称为广义线性模型（generalized linear model），$g(\cdot)$为联系函数（link function）。

对数几率回归

上述讨论的是回归模型，对于分类问题，线性回归模型依旧适用，只需要找到一个单调可微函数将分类任务的标记和模型的预测值联系起来即可。

二分类任务中其输出标记只有0和1两类，而线性回归模型的输出值$z=\pmb{w}^T\pmb{x}+b$为实数值，将$z$转换为0或1值最简单的方法是单位阶跃函数（unit-step function），如下图所示。

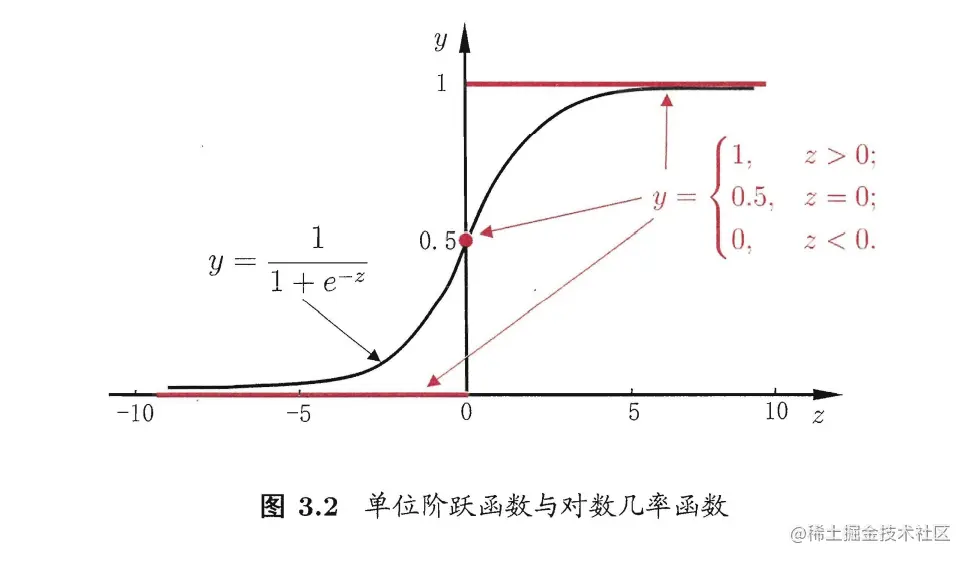
但有一个问题在于这个函数不连续，不能代入$g(\cdot)$，因此找到了对数几率函数（(logistic function）来替代单位阶跃函数，函数表达式如下：

如图3.2所示，对数几率函数是一种sigmoid函数（即S形函数），将对数几率函数作为$g(\cdot)$可得到：

将$y$视为样本$\pmb{x}$为某类的可能性，则$1-y$是另一类的几率，两个比值$\frac{y}{1-y}$则可称为几率（odds），对几率取对数则得到对数几率（logit）。

使用对数几率的模型就是对数几率（(logistic regression）回归模型，基于上式求解$\pmb{w},b$的方法：

按照前面说的逻辑，将y视为一类的后验概率估计$p(y=1|\pmb{x})$，重写式子为：

从$y=\frac{1}{1+e^{-(\pmb{w}^T\pmb{x}+b)}}$可知：

基于上式可通过极大似然法（maximum likelihood method）来估计参数，即令每个样本属于其真实标记的概率越大越好。对于数据集$\{(\pmb{x}_i,y_i)\}^m_{i=1}$，其对数几率回归模型最大化对数似然：

令$\beta = (\pmb{w};b),\hat{\pmb{x}}=(\pmb{x};1)$，则$\pmb{w}^T\pmb{x}+b=\beta^T\hat{\pmb{x}}$。

令$p_1(\hat{{\pmb{x}}};\beta)=p(y=1|\pmb{x}),p_0(\hat{{\pmb{x}}};\beta)=p(y=0|\pmb{x})$，则可得到：

综合上述内容可得：

最小化上式即可求解参数：

上式为关于$\beta$的可导连续凸函数，用梯度下降法、牛顿法均可求解出其最优解。

Linear Discriminant Analysis, LDA 线性判别分析

LDA的基本思想很简单，给点样本集将样本投影到一条直线上并使同类样本尽可能接近，在测试中将测试样本同样投影到这条直线上，根据投影点的位置来确定其分类，如下图所示：

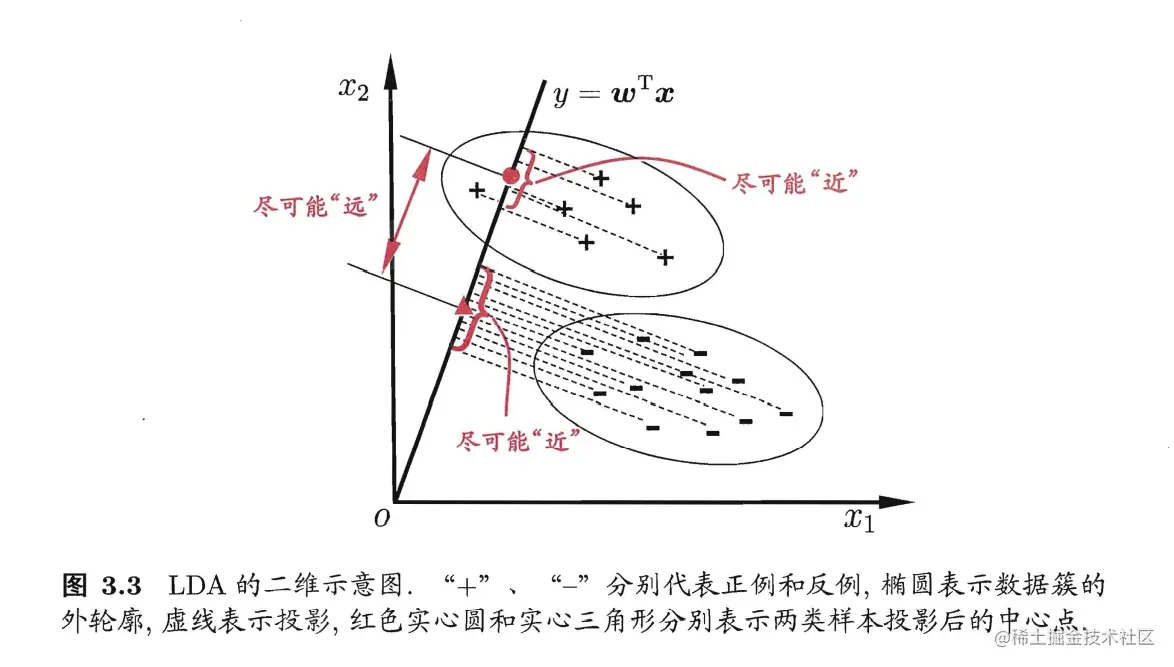
用$X_i,\pmb{\mu}_i,\pmb{\Sigma}_i$表示第i类的样本集合（例子中为二分类，0和1）、均值向量和协方差矩阵。若将样本投影到直线$y=\pmb{w}^T\pmb{x}$上，则两类样本的投影分别为$\pmb{w}^T\pmb{\mu}_0,\pmb{w}^T\pmb{\mu}_1$。所有样本点都投影到直线上得到的两类样本协方差（推导过程）为$\pmb{w}^T\pmb{\Sigma}_0\pmb{w},\pmb{w}^T\pmb{\Sigma}_1\pmb{w}$，直线是一维空间所以上述值都为实数。

投影的目标有两个：

• 让同类样例投影点的协方差尽可能的小，即让$\pmb{w}^T\pmb{\Sigma}_0\pmb{w}+\pmb{w}^T\pmb{\Sigma}_1\pmb{w}$最小化。
• 让异类样本投影点尽可能得远，即让$||\pmb{w}^T\pmb{\mu}_0-\pmb{w}^T\pmb{\mu}_1||^2_2$（向量的欧式距离）最大化。

综上可以得到目标函数$J$，优化问题的目标是让$J$最大化：

定义类内散度矩阵（withi-class scatter matrix），它表示某类内样本的投影后的离散程度：

定义类间散度矩阵（between-class scatter matrix）用于衡量两个类中心点间的距离：

上面的推导过程可见链接

目标函数$J$可重写为：

从$J$可看出，当$\pmb{w}$成比例放大或缩小时目标函数是保持不变的，因此目标函数只被$\pmb{w}$的方向影响，为简化计算假设$\pmb{w}^T\pmb{S}_w\pmb{w}=1$。

则问题转化为：

通过拉格朗日乘子法得到：

通过对$F(\pmb{w})$求$\pmb{w}$的偏导并令其等于0可得到下式：

$\pmb{S}_w$若可逆则可直接求得：

若矩阵为奇异矩阵，则需要对$\pmb{S}_w$使用奇异值分解来求得$\pmb{S}_w^{-1}$。

多分类学习

多分类学习中通常通过对多分类任务进行拆分来解决多分类问题，方法包括：

• 一对一（ONE vs ONE, OvO）
• 一对其余（ONE vs REST, OvR）
• 多对多（MANY vs Many, MvM）

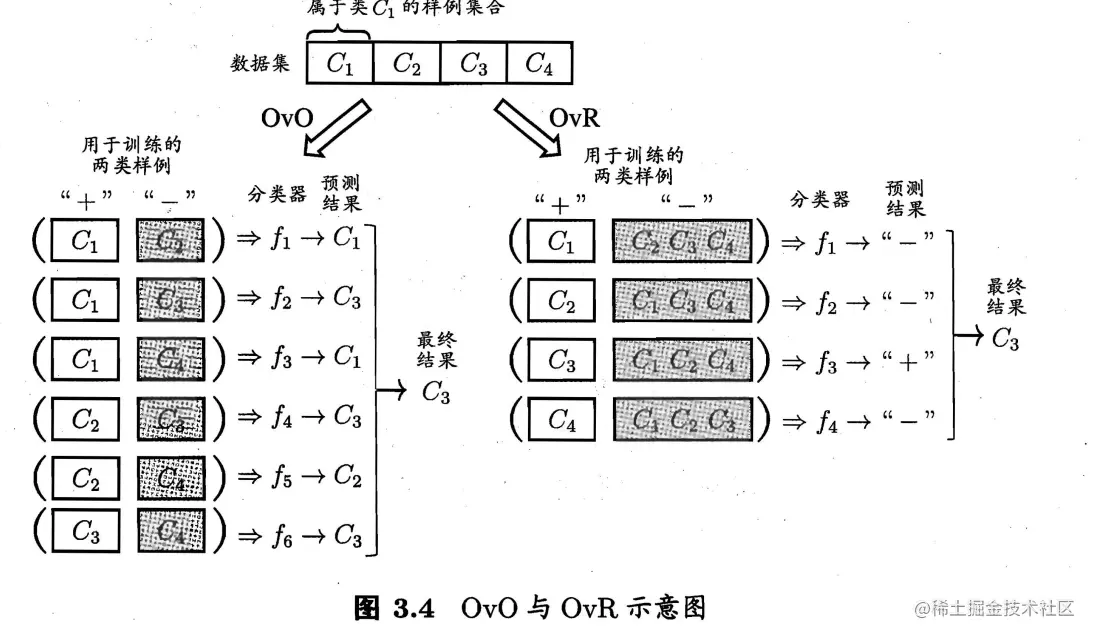
class-imbalance 类别不平衡

某些分类任务中会出现分类分布不平衡的情况，例如某分类998个另一类只有2个，这样学习方法若构建了一个永远只返回大类分类结果的学习器，那准确率可达99.8%，显然这样的学习器是没有意义的，分布不平衡中人们通常会更关心小样本分类的准确率。

rescaling 再缩放

再缩放策略通过改变之前提过的几率$\frac{y}{1-y}$来解决类别不平衡问题，具体做法为：

用$m+,m-$表示两类不同样本的数目，假设训练集是真实样本总体的无偏采样（即真实样本的类别比例在训练样本中得以保持）则可构建新的几率：

其他方法

再缩放方法虽然简单但是训练样本往往很难保证其反应的是真实的分布，因此还有其他解决办法：

• 欠采样（undersampling）：通过去除大类中多的样本来使各类样本数接近
• 过采样（oversampling）：通过增加一些小类中的样本来使各类样本数接近
• 阈值移植（threshold-moving）：直接基于原始训练集学习，在预测时再将$\frac{y'}{1-y'}$嵌入到决策过程中。