JAVA-数据结构与算法-平衡二叉树（AVL树）和多路查找树（介绍）

99永远差一分
293 阅读5分钟

写在前面

平衡二叉树

  • 平衡二叉搜索树，是一个空树，或者它的左右两个子树的高度差的绝对值不能超过1，并且左右两个子树都是一棵平衡二叉树，具体实现为红黑树、AVL、替罪羊树、Treap、伸展树等
  • 以下方法都实现在节点中

左右旋

  • 左旋转
private void leftRotate() {
    Node newNode = new Node(value);
    //把新的节点的左子树设置成当前节点的左子树
    newNode.left = left;
    //把新的节点的右子树设置成当前节点的右子节点的左子树
    newNode.right = right.left;
    //把当前节点的值，替换成右子节点的值
    value = right.value;
    //把当前节点的右子树设置成当前节点的右子节点的右子树
    right = right.right;
    //把当前节点的左子树设置成新的节点
    left = newNode;
}
  • 右旋转
private void rightRotate() {
    Node newNode = new Node(value);
    //把新的节点的右子树设置成当前节点的右子树
    newNode.right = right;
    //把新的节点的左子树设置成当前节点的左子节点的右子树
    newNode.left = left.right;
    //把当前节点的值，替换成左子节点的值
    value = left.value;
    //把当前节点的左子树设置成当前节点的左子节点的左子树
    left = left.left;
    //把当前节点的右子树设置成新的节点
    right = newNode;
}

获取节点高度

  • 返回左子树的高度
public int leftHeight() {
    if (left == null) {
        return 0;
    }
    return left.height();
}
  • 返回右子树的高度
public int rightHeight() {
    if (right == null) {
        return 0;
    }
    return right.height();
}
  • 返回当前节点的高度，以该节点为根节点的树的高度
public int height() {
    //加上1为加上自身这个节点
    return Math.max(left == null ? 0 : left.height(),
            right == null ? 0 : right.height()) + 1;
}

双旋转

  • 每次添加完毕后，都对当前节点进行平衡树处理，写在add方法中
  • 双旋转，举例当进行右旋转时，如果当前节点的左子节点的右子树高度大于左子树的高度，那么转换完成后，右子树高度仍会大于左子树高度
  • 那么，就要先对左子节点进行左旋转，减小左子节点的右子树的高度
  • 并且，如果左子树大于右子树的高度，由于每次右旋转都会减少左子树的节点数量，所以只需要一直旋转就好
boolean flag = false;
//当添加完节点后，如果右子树的高度 - 左子树的高度 > 1
while (rightHeight() - leftHeight() > 1) {
    //如果右子节点的左子树高度大于右子节点的右子树的高度
    if (right != null && right.leftHeight() > right.rightHeight()) {
        right.rightRotate();
        leftRotate();
    } else {
        leftRotate();
    }
    //因为对于一棵树来说，左右子树不平衡只有其中一种情况，如果处理完成后直接跳出即可
    flag = true;
}
if (flag) {
    System.out.println(this.right);
    System.out.println(this.left);
    return;
}
//右旋转
while (leftHeight() - rightHeight() > 1) {
    //如果左子节点的右子树高度大于左子节点的左子树的高度
    if(left != null && left.rightHeight() > left.leftHeight()) {
        left.leftRotate();
        rightRotate();
    } else {
        rightRotate();
    }
}

多路查找树

  • 二叉树，操作效率高，需要加载到内存，但是如果节点海量，操作速度慢，构建二叉树时，多次进行IO操作，速度有影响
  • 多叉树，每个节点有更多的数据项和更多的子节点
  • B(B+)树，通过重新组织节点，降低树的高度，应用在文件存储系统和数据库系统
  • 节点的度，子树的个数；树的度，所有节点中，节点度最大的值

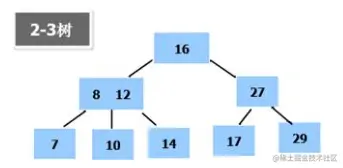
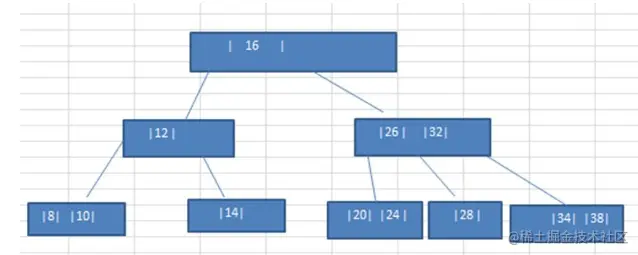
2-3树

  • 是最简单的B树结构，所有叶子节点都在同一层（B树都满足这个条件），由二节点和三节点构成
  • 有两个子节点的节点叫二节点，二节点要么没有子节点，要么有三个子节点
  • 有三个子节点的节点叫三节点，三节点要么没有子节点，要么有三个子节点
  • 对于一个三节点，这个三节点有两个值，左子节点小于这两个值，中间子节点介于两个值之间，右子节点大于这两个值
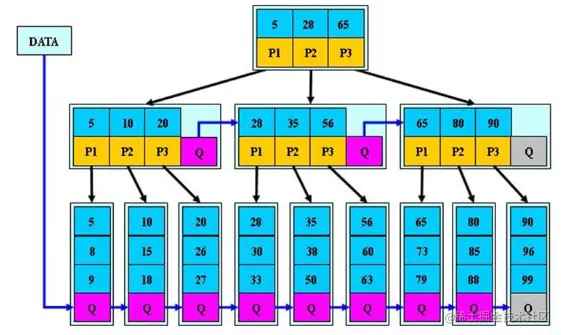
  • 234树，有四节点，放四个值，并且有四个字节点 image.png image.png

B树

  • B-tree，B-树
  • B树的阶，节点最多的子节点的个数
  • B树搜索，从根节点开始，对节点内的关键字有序序列进行二分查找，命中则结束，否则向下查找
  • 关键字集合分布在整棵树中，关键字可能在叶子节点，也可能在非叶子节点中
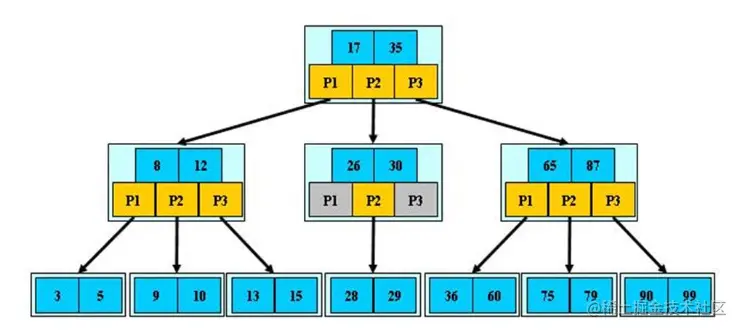
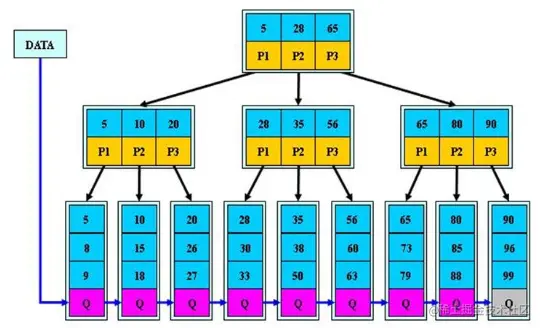
  • 搜索性能等价于在关键字全集内存一次二分查找 image.png

B+树

  • 所有的数组都放在叶子节点，稠密索引，叶子节点存的形式为链表，链表中的关键字数据都是有序的
  • 非叶子节点相当于是叶子节点的索引，稀疏索引
  • 叶子节点相当于是存储关键字数据的数据层
  • 适合文件索引系统
  • 将一段长链表数据，分割成好几段
  • 分裂，当一个节点的数据满时，创造新节点，分配数据；或者分配给其他兄弟节点（对于B*树）
  • B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针； image.png

B*树

  • B+树的变体，在B+树的非根和非叶子节点在增加指向兄弟的指针
  • B*树定义了非叶子节点关键字个数至少为(2/3)*M，块最低使用率为2/3，B+树的块的最低使用率为1/2
  • 块的利用率，指的是叶子节点的存储空间
  • B*树分配新节点的概率比B+树要低，空间使用率更高
  • B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针； image.png
avatar
文章
阅读
粉丝