LeetCode96. 不同的二叉搜索树

$\color{DodgerBlue}{1.题目描述}$

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

难度：中等

示例 1：

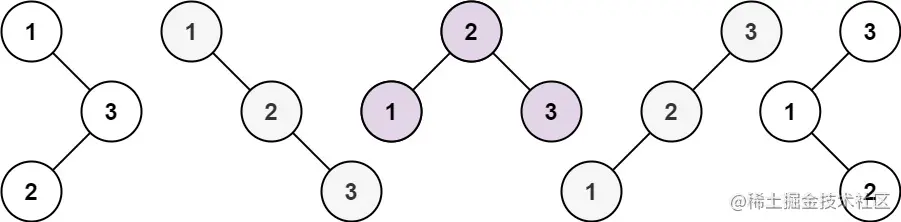
输入： n = 3
输出： 5

示例 2：

输入： n = 1
输出： 1

$\color{DodgerBlue}{2.解题思路}$

1. $1-n$ 的整数，每一个整数都可以作为一个根节点，然后左右两个子树又可以作为二叉搜索树的情况
2. 于是可以利用动态规划来，将问题逐步分解下去
3. 假设$G(n)$表示我们要求的$1-n$ 的互不相同的二叉搜索树的种树 $F(i)$为节点i作为根节点的二叉搜索树的种树，则 $G(n) = F(1)+F(2)+...+F(i)...+F(n)$

4. i节点作为根的时候，左右子树分别为 $[1...i-1]$ 和 $[i+1...n]$，它们的二叉树种树分别为 $G(i-1),G(n-i)$
5. 所以 $F(i) = G(i-1)*G(n-i)$，情况数为左右两个子树的乘积
6. 于是可以得出 $G(n) = \sum[G(i-1)*G(n-i)], 1<=i<=n$ (这里是最终的求和数学公式)
7. $G(n) = [G(0)G(n-1)] + [G(1)G(n-2)] + [G(2)G(n-3)] + ... + [G(n-2)G(1)] + [G(n-1)G(0)]$

8. 对于初始边界，当为空树或者只有一个节点的时候，$G(0) = G(1) = 1$, 只有一种情况
9. ref:leetcode-cn.com/problems/un…

$\color{DodgerBlue}{3.JavaScript代码}$

/**
 * @param {number} n
 * @return {number}
 */
var numTrees = function(n) {
    let dp = new Array(n + 1).fill(0)
    dp[0] = 1
    dp[1] = 1
    for(let j = 2; j <= n; j++){ // 因为0和1已知，要求dp(n), 所以j从2开始算
        for(let i = 1; i <= j; i++) { 
            dp[j] += dp[i-1] * dp[j-i] 
        }
    }
    return dp[n]
};