【翻译】状态空间模型综述原文链接这篇文章中总结了一些著名的状态空间模型，所有的模型都源自贝叶斯滤波器。贝叶斯滤波器

这篇文章中总结了一些著名的状态空间模型，所有的模型都源自贝叶斯滤波器。

贝叶斯滤波器

这些模型中考虑了两个随机过程，一是状态 $x_t$ ，二是观测值或测量值 $y_t$ ，此处的 $t$ 表示时间，但随机过程总体上不局限于时间序列。我们想获得的是状态的真值，但是仅能观察到观测值的值。因此，状态空间模型的目标在于基于观测值估测状态值，应该处理两个关系：

状态-状态的概率 $P(x_t|x_{1:t-1})$ （下标 $1:t-1$ 表示从第1个到第t-1个状态）

状态-观测值的概率 $P(y_t|x_t)$ ，任意两个观测值之间不存在直接关系，一个常用的假设是马尔科夫性质（Markov Property），它假设现在的状态仅依赖于上一个状态，即 $P(x_t|x_{1:t-1})=P(x_t|x_{t-1})$ 。

预测和更新

状态空间模型用于在线算法包含递归两个步骤，预测和更新。

预测这一步中，基于分布 $p(x_{t-1}|y_{1:t-1})$ 和状态-状态概率 $P(x_t|x_{t-1})$ 来估算后验分布 $p(x_t|y_{1:t-1})$ ，其数学表达为：

p(x_t|y_{1:t-1})=\int p(x_t|x_{t-1})p(x_{t-1}|y_{1:t-1})dx_{t-1}

更新这一步中，基于最新的观测值 $y_t$ 来更新先验分布，数学表达为（ $\propto$ 表示成正比）：

p(x_t|y_{1:t})=p(y_t|x_t)p(x_t|y_{1:t-1})/p(y_t)\propto p(y_t|x_t)p(x_t|y_{1:t-1})

建模中的思考

贝叶斯滤波器通过后验分布 $p(x_t|y_{1:t})$ 来估算 $x_t$ ，通常状态-状态概率和状态-观测值概率在实际建模问题中的不能直接获得的，反而他们应该从预测模型 $x_t=f(x_{t-1})$ 和度量模型 $y_t=g(x_t)$ 中推测出来。因此有一系列问题需要回答：

状态 $x_t$ 是连续的还是离散的？
$x_t$ 的分布是什么？
问题是线性的还是非线性的？
度量模型是线性的还是非线性的？

基于这些问题，使用下图中不同的滤波器：

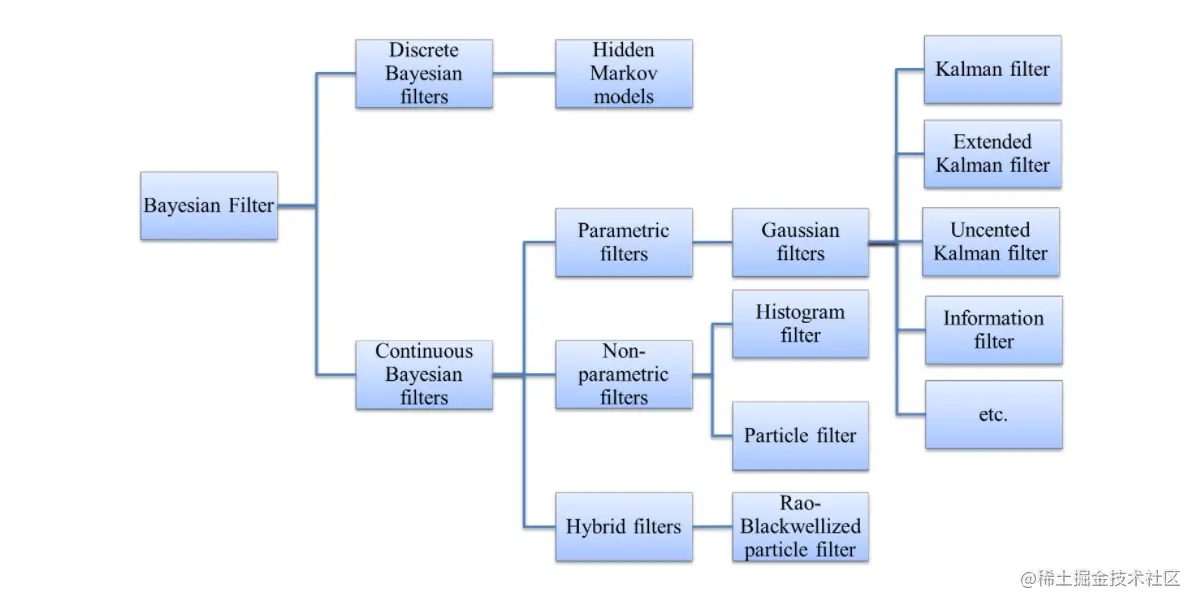
贝叶斯滤波器分类

根据状态 $x_t$ 是离散的还是连续的，贝叶斯滤波器可以分成离散滤波器和连续滤波器，当状态 $x_t$ 只有离散值时，状态-状态概率可以被表示为转移概率矩阵（transition matrix）： $A=[a_{i,j}],a_{i,j}=P(x_t=j|x_{t-1}=i)$ 。

根据 $x_t$ 的分布是否被假设为一个特定的形式，贝叶斯滤波器可以被分成有参数滤波器和无参数滤波器。如在高斯滤波器中， $x_t$ 的分布被假设为一个多元正态分布，根据该假设，后验分布 $P(x_t|y_{1:t})$ 可以用严谨的形式来表达。

另一方面，无参数滤波器不对 $x_t$ 的分布做任何假设，而是用一些技巧来近似这些分布，例如 $x_t$ 的分布可以被表示为一个直方图（直方图滤波器）或从目标分布中抽取的一堆样本（粒子滤波器）。无参数滤波器近似分布，对预测模型 $x_t=f(x_{t-1})$ 和度量模型 $t_t=g(x_t)$ 没有限制，因此可以灵活使用在多种场景中。然而，由于缺乏严谨的形式导致其计算量会很大，近似越好算力负担越重。

一些滤波器分类的简单介绍：

高斯滤波器假设 $x_t$ 的分布为一个多元正态分布。
在经典卡尔曼滤波中，为保持正态性，预测模型 $x_t=f(x_{t-1})$ 及度量模型 $y_t=g(x_t)$ 被假设为线性的， $x_t=Ax_{t-1}+\epsilon_t,y_t=Bx_t+\delta_t$ 。
一些卡尔曼滤波器例如扩展卡尔曼滤波和无分卡尔曼滤波等不使用线性关系假设，而是通过泰勒展开等线性化技术进行近似。
信息滤波器及其衍生滤波器本质是和卡尔曼滤波器相同，使用多元正态分布的信息表示： $\Omega=\Sigma^{-1},\xi=\Omega\mu$ 。
混合滤波器是有参数和非参数滤波器的混合，它其中一些状态的维度假设为特定格式，而另一些则用非参数的方法表示。