【翻译】从向量到函数——变换、基和核方法

原文链接

什么是函数

一切想法的起源来自：一个函数实际上是一个无限的向量，如下图所示：

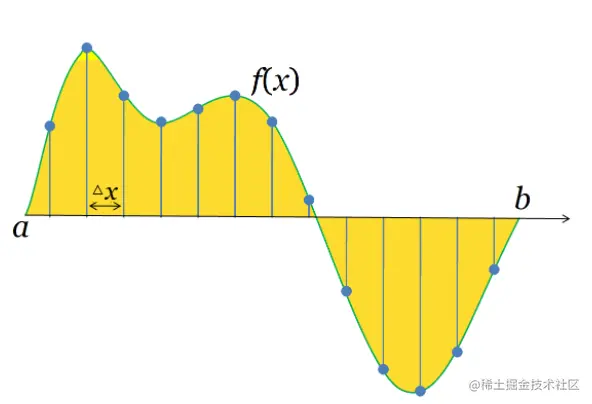
对于一个定义在区间$[a,b]$内的函数，根据间隔$\Delta x$取样本，如果在点$[a,x_1,...,x_n,b]$处取函数$f(x)$的样本，然后就可以把函数变换为一个向量$(f(a),f(x_1),...,f(x_n),f(b))^T$，当$\Delta x \rightarrow 0$时，这个向量会越来越接近原函数，最终变成无限向量。

上述的分析中假设$x$是一个实数，但是当$x$是一个向量时，它依旧适用。接下来使用$\mathbf{x}$来表示$R^n$空间中的法向量，用$f$来表示函数本身，也就是一个无限向量。用$f(\mathbf{x})$来表示函数在点$\mathbf{x}$处的函数值，为一个实数。

函数内积

函数是一个无限向量，而向量有内积，因此对于两个向量$\mathbf{x}=(x_1,...,x_n)$和$\mathbf{y}=(y_1,...,y_n)$，其内积定义为：

根据上面的公式一般人会想到，对应的函数的内积可以定义为：

但是这个公式存在一些问题，当$\Delta x \rightarrow 0$时，这个公式中$f$和$g$的维度变大了，公式无法收敛。（因为向量的维度是离散的，因此可以通过累加离散的值计算内积，而函数是连续的），因此通过微积分的方法计算函数内积：

基

内积的含义是什么？如下图所示，对于两个向量$A,B$，内积表示一个向量到另一个的投影长度。

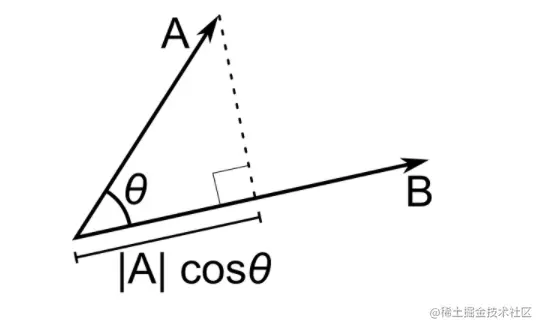
公式可以表达为:

可知：

若向量$B$为单位向量（长度为1个单位），则内积就是在$B$上投影的坐标。因此给定一组正交基向量$\{e_i\}^n_{i=1}$，即$<e_i,e_j>=0$且$|e_i|=1$。这些基向量可以通过线性操作构造一个空间，任何向量$\mathbf{x}$都可以由基向量表达：

若$|e_i|\neq 1$则：

类似的，函数也有基，它们可以是正交或非正交的。若定义了函数基的集合，那空间中任意函数也可以由基函数的组合表示。函数内积同样可以在任何特殊集上被用于计算系数。特殊的是，由于函数的维数是连续的，就可能存在无限的基函数。

对于一个函数基组$\{h_i\}$，若$<h_i,h_j>=0$且$|h_i|\neq 1$，任何空间内的函数可以被表示为：

若$|h_i|\neq 1$则：

例子：变换

令基函数$\{h_p\}$（$p$是一个实数）为：

函数定于在区间$[0,T]$上，此处用$p$来表示基函数的索引，用来区分虚数$i$，可以证明任意两个基函数是正交的(对于复数，计算内积时，后一项应取共轭转置)：

当$p \neq q$且$a+\bar{b}i=a-bi$时，基的长度为：

对于定义在该空间中的区间$[0,T]$上的函数$f(x)$可以写作：

系数$c_p$可以由下面的方法求出：

这就是傅里叶级数的计算过程。

例子：核函数

令：$K(x,y)=h_y(x)$

基函数的集合可以被定义为一个带两参数的函数$K$，例子中的$y$是离散的。但是这并不是所有的空间，若将$y$定义为实数，则可以表示空间内的任何函数。

函数$k(x,y)$为核函数，它可以被看作是一个基函数的集群，若对于任意$y_1 \neq y_2$他们是正交的$<K(\cdot,y_1),K(\cdot,y_2)>=0$，且基$|K(\cdot,y)|^2=\int 1dx$，则任何函数$f$可以表示为：

则函数$f$基于基$K(\cdot,y)$的系数可以通过下面的方法计算：

因此核函数可以用于将任何函数转化仅另一个空间（一个函数空间）。

例子：转换

令核函数为：

此处的$i$为虚数，可以简单证明任意两个核函数是正交的：

当$y_1 \neq y_2$，基平方的长度为：

这构造了一个完整的函数空间，其系数可以通过下式计算：

原函数可以表示为：