写在前面

• 数据结构与算法全文

栈的三种表达式

前缀表达式

• 波兰表达式
• 运算符位于操作数之前

流程

• (3+4)*5-6 -> - * + 3 4 5 6
• 从右至左扫描，将6 5 4 3压入栈
• 遇到+运算符弹出3 4，3为栈顶，4为次顶，计算得7，压入栈
• 接下来*，弹出7 5，计算得35，再入栈
• 最后-，弹出35 6，最终结果29

中缀表达式

• 常见的运算方式，但是对于计算机来说并不好操作
• (3+4)*5-6

后缀表达式

• 逆波兰表达式，运算符位于操作数之后
• (3+4)*5-6 -> 3 4 + 5 * 6 -

流程

• 从左至右扫描，将3 4压入栈
• 遇到+，弹出4 3，4为栈顶，3为次顶，得7入栈
• 5入栈
• 遇到*，弹出5 7得35，入栈
• 最后-，弹出6 35，但是栈底35减去6，得29

逆波兰计算器

• 使用

//`(30+4)*5-6`
String suffixExpression = "30 4 + 5 * 6 -";
//先将表达式放入list中
System.out.println(calculate(getListString(suffixExpression)));

//将逆波兰表达式，依次放入list
public static List<String> getListString(String suffixExpression) {
    String[] split = suffixExpression.split(" ");
    ArrayList<String> list = new ArrayList<>();
    for (String s : split) {
        list.add(s);
    }
    return list;
}

public static int calculate(List<String> list) {
    Stack<String> stack = new Stack<>();
    for (String s : list) {
        //使用正则表达式取出
        if (s.matches("\d+")) {
            stack.push(s);            
            } else {
            //遇到运算符
            int num2 = Integer.parseInt(stack.pop());
            int num1 = Integer.parseInt(stack.pop());
            int res = 0;
            if (s.equals("+")) {
                res = num1 + num2;
            } else if (s.equals("-")) {
                res = num1 - num2;
            } else if (s.equals("*")) {
                res = num1 * num2;
            } else if (s.equals("/")) {
                res = num1 / num2;
            } else {
                throw new RuntimeException("error");
            }
            //结果入栈
            stack.push("" + res);
        }
    }
    return Integer.parseInt(stack.pop());
}

中缀表达式转换成后缀表达式

• 扫描完毕后执行7，s2栈的逆序为需要的后缀表达式

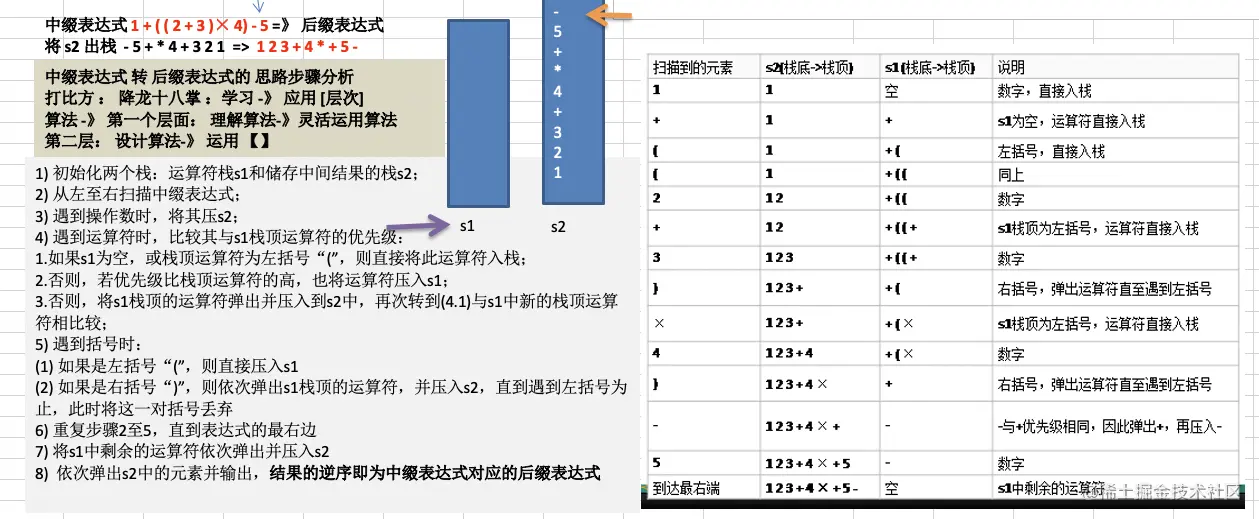
代码实现

• 小数的处理，通过正则表达式进行筛选 s.matches("\d+\.\d+") || s.matches("\d+")
• 表达式中的空格处理expression = expression.replace(" ", "");
• 将中缀表达式转换成list

public static List<String> toInfixExpressionList(String expression) {
    List<String> list = new ArrayList<>();
    //用于遍历expression
    int i = 0;
    //拼接
    String str;
    //每遍历到一个字符，放入c
    char c;
    do {
        //如果非数字，加入到list
        //ascii 48～57 为数据
        if (((c = expression.charAt(i)) < 48) || ((c = expression.charAt(i)) > 57)) {
            list.add("" + c);
            i ++;
        } else {
            //多位数
            str = ""; //清空
            while (i < expression.length()
                    && ((((c = expression.charAt(i)) >= 48) && ((c = expression.charAt(i)) <= 57))
                        || ((c = expression.charAt(i)) == 46))) {
                        //46为小数点
                str += c;
                i++;
            }
            list.add(str);
        }
    } while (i < expression.length());
    return list;
}

• 中缀表达式list转换成后缀表达式list

public static List<String> parseSuffixExpressionList(List<String> list) {
    Stack<String> stack = new Stack<>();
    //不通过中间栈，在进行逆序处理，直接输出到list中，就是需要的逆波兰表达式
    List<String> resList = new ArrayList<>();
    for (String s : list) {
        if (s.matches("\d+\.\d+") || s.matches("\d+")) {
            //数字
            resList.add(s);
        } else if (s.equals("(")) {
            stack.push(s);
        } else if(s.equals(")")) {
            while (!stack.peek().equals("(")) {
                resList.add(stack.pop());
            }
            //去掉左括号
            stack.pop();
        } else {
            //优先级
            //s的优先级小于等于栈顶优先级，栈顶的运算符弹出加入到list
            while (stack.size() != 0  && Operation.getValue(stack.peek()) >= Operation.getValue(s)) {
                resList.add(stack.pop());
            }
            //将s最后加入
            stack.push(s);
        }
    }
    //处理剩余的操作符
    while (stack.size() != 0){
        resList.add(stack.pop());
    }
    return resList;
}

• 处理运算符优先级

class Operation{
    private static int ADD = 1;
    private static int SUB = 1;
    private static int MUL = 2;
    private static int DIV = 2;
    private static int LEFTPARE = 0;
    //返回对应优先级
    public static int getValue(String operation) {
        int res = 0;
        switch (operation) {
            case "+":
                res = ADD;
                break;
            case "-":
                res = SUB;
                break;
            case "*":
                res = MUL;
                break;
            case "/":
                res = DIV;
                break;
            case "(":
                res = LEFTPARE;
                break;
            default:
                System.out.println("Operation is error.");
                break;
        }
        return res;
    }
}

• 计算

public static double calculate(List<String> list) {
    Stack<String> stack = new Stack<>();
    for (String s : list) {
        //使用正则表达式取出
        if (s.matches("\d+\.\d+") || s.matches("\d+")) {
            stack.push(s);
        } else {
            //遇到运算符
            double num2 = Double.parseDouble(stack.pop());
            double num1 = Double.parseDouble(stack.pop());
            double res = 0;
            if (s.equals("+")) {
                res = num1 + num2;
            } else if (s.equals("-")) {
                res = num1 - num2;
            } else if (s.equals("*")) {
                res = num1 * num2;
            } else if (s.equals("/")) {
                res = num1 / num2;
            } else {
                throw new RuntimeException("error");
            }
            //结果入栈
            stack.push("" + res);
        }
    }
    return Double.parseDouble(stack.pop());
}