这是我参与8月更文挑战的第31天,活动详情查看:8月更文挑战
神经网络的表示
都有线性回归和逻辑回归了为什么还要学神经网络呢?
现在举几个例子。
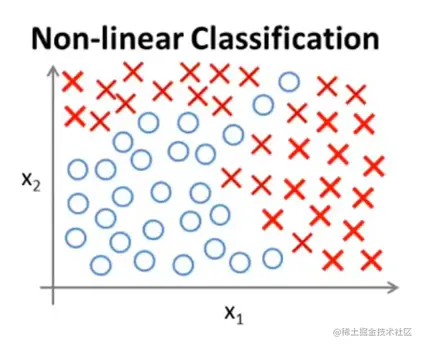
这是一个监督学习的分类问题。只有两个特征量。
如果你使用逻辑回归,想拟合出下面的曲线,那你可能需要很多项式才能将正负样本分开。
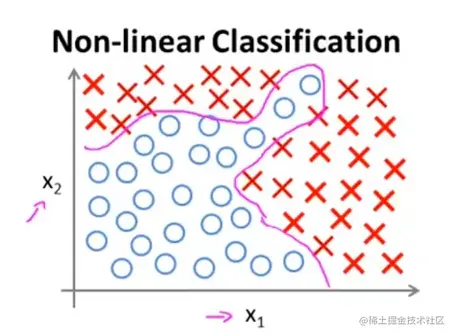
g(θ0+θ1x1+θ2x2+θ3x1x2+θ4x12x2+θ5x13x2+θ6x1x22+…)
只是两个特征量就如此麻烦,那要是100个特征量呢?
就算只包含二次项,比如x12、x22、...、x1002、x1x2、x1x3、...、x99x100,这样最终也有5000多个多项式。
大约是2n2个,x1从x1乘到x100就是100项,以此类推最后x100从x1乘到x100加起来就是10000项。但是x1x100和x100x1是一样的,再合并一下相同的。所以最后大概剩下一半。
现在已经5000多项了,最后的结果很可能会过拟合,并且还会存在运算量过大的问题。
现在算一下包括三次项的。
x13、x23、...、x1003、x12x2、x12x3、...、x99x1002,这样最后就有170000个三次项。(自己验证,我不推了)。
上边的例子可以知道,当特征量很大的时候就会造成空间急剧膨胀。因此特征量n很大的时候用构造多项式的方法来建立非线性分类器是很不明智的选择!
然而现实中对于很多机器学习的实际问题,特征量个数n一般都特别大。
比如对于计算机视觉的问题:现在你需要通过机器学习来判断图像是否是一个汽车。

你肉眼看到之后就能知道这是一个汽车,但是及其肯定不能一下就知道这是汽车。
 取这一小块。在你眼里是个门把手,但是及其只能识别出像素强度值的网格,知道每个像素的亮度值。因此计算机视觉的问题就是根据像素点的亮度矩阵告诉我们这个矩阵代表一个汽车的门把手。
取这一小块。在你眼里是个门把手,但是及其只能识别出像素强度值的网格,知道每个像素的亮度值。因此计算机视觉的问题就是根据像素点的亮度矩阵告诉我们这个矩阵代表一个汽车的门把手。
当我们用机器学习后造一个汽车识别器的时候,我们要做的就是提供一个带标签的样本。其中一部分是车,另一部分样本不是车。将这样的样本集输入给学习算法,从而训练场出一个分类器,最后输入一个新图片,让分类器来判定这是个什么东西。

引入非线性假设的必要性:
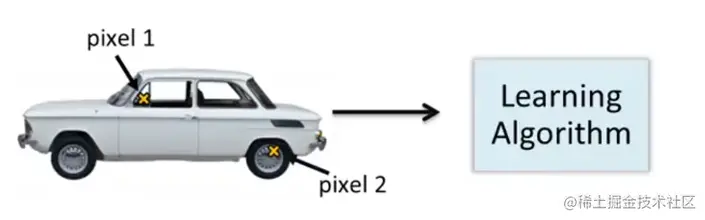
一个车,取两个像素点,将其放到坐标系中。位置取决于像素点12的强度。
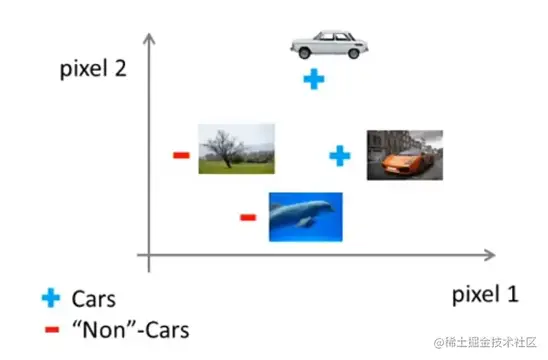
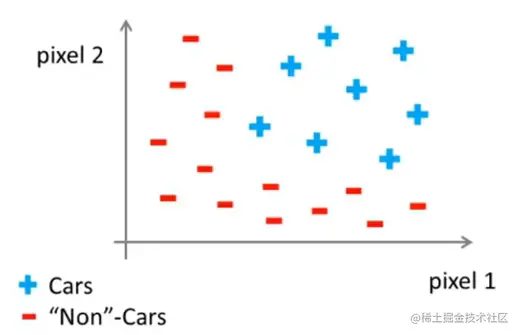
现在我们需要一个非线性假设来区分这两类样本。
假设车子图片是50*50像素,现在用x向量存储每个像素点的亮度。那这样就有2500个像素点。向量的维度就是2500.如果图片是彩色的,用RGB存储,那向量的维度就是7500。
如果现在要想用包含所有的二次项来列出非线性假设,那Quadratic features (xi×xj):≈3 million features。三百万,计算成本太高了。因此只包含平方项、立方项找偶记回归假设模型只适合n比较小的情况。n较大的情况下,即在复杂的非线性假设上神经网络的效果更为优异。
神经网络算法已经很久了,起初是为了制造能模拟大脑的机器。
模型展示
神经网络模仿了大脑中的神经元。神经元有轴突和树突。轴突相当于输入路线,树突相当于输出路线。神经元就可以看做是一个计算单元。神经元之间
用电流进行交流。(emmm作为一个生物学的学生我居然还清楚地记得这些知识……)
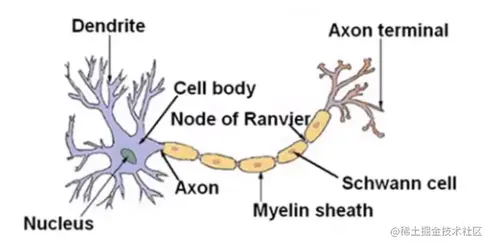
在一个人工实现的神经网络里,用下图一个简单的模型来模拟神经元工作。
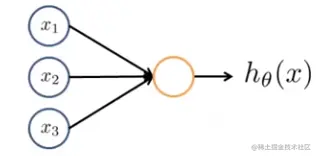
x1−x3表示树突作为输入端,右边则作为轴突输出预测模型。
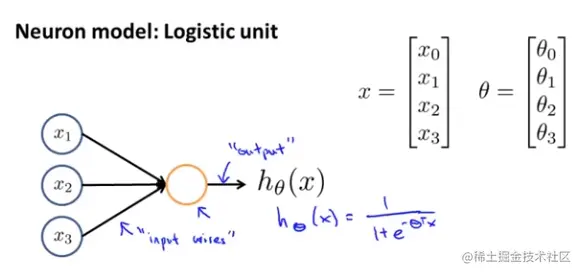
输入是x1−x3但通常会加上额外节点x0,成为偏置单元(bias unit)或者偏置神经元(bias neuron)。
在神经网络的文献中如果看到权重(weight)这个词,他其实和摸清参数θ是同一个东西。
人类的神经网络是一组神经元,下图是一个更复杂的图像,他的第一层蓝色圈圈被称为输入层,因为我们在第一层输入特征量。最后一层的黄色圈圈被称为输出层,因为这一层神经元输出假设的最终计算结果,中间的第二层被称位隐藏层,隐藏层可以不止一层。
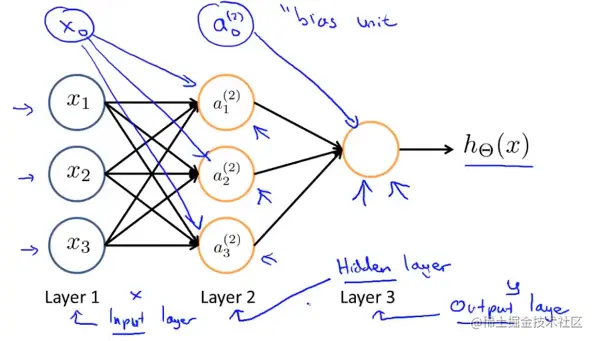

ai(j)=Θ(j)= "activation" of unit i in layer j matrix of weights controlling function mapping from layer j to layer j+1
ai(j)表示第j层第i个神经元或者单元的激活项,至于权重矩阵Θ(j),控制第j层到j+1层的映射关系。
a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)hΘ(x)=a1(3)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
a1(2)的激活函数a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
上一张小图里没有加上偏置单元,看上上个图加上偏置神经元的那个图。这里边Θ(1)矩阵代表的就是第一层(输入层x)到第二层隐藏层a(2)的权重(参数)矩阵。
可以理解为Θ(1)=⎣⎡θ10θ11θ12θ13θ20θ21θ22θ23θ30θ31θ32θ33⎦⎤
取这一小块。在你眼里是个门把手,但是及其只能识别出像素强度值的网格,知道每个像素的亮度值。因此计算机视觉的问题就是根据像素点的亮度矩阵告诉我们这个矩阵代表一个汽车的门把手。