机器学习系列--kmeans分类算法
简介
K-means算法是集简单和经典于一身的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为类簇是由距离靠近的对象组成的,因为把得到紧凑且独立的簇作为最终目标。
算法
核心思想
通过迭代寻找k个类簇的一种划分方案,使得用这k个类簇的均值来代表相应各类样本时所得的总体误差最小。
k个聚类具有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。k-means算法的基础是最小误差平方和准则
步骤
将样本聚类成k个簇,其中k是用户给定的,其求解过程非常直观简单
1.随机选取k个聚类质心点
2.重复下面过程直到收敛
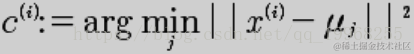
对于每一个样例 i,计算其应该属于的类
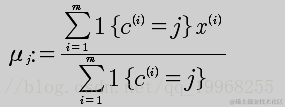
对于每一个类 j,重新计算该类的质心
伪代码
1.创建k个点作为初始的质心点(随机选择)
2.当任意一个点的簇分配结果发生改变时
对数据集中的每一个数据点 对每一个质心 计算质心与数据点的距离 将数据点分配到距离最近的簇(分组) 对每一个簇,计算簇中所有点的均值,并将均值作为质心 (新的均值等于原均值时候跳出迭代输出划分)
特点
各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开
k-means算法的基础是最小误差平方和准则
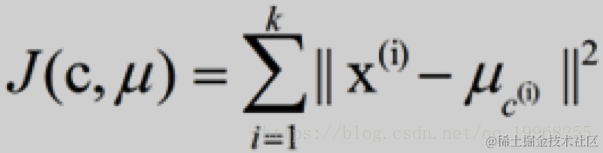
μc(i)表示第i个聚类的均值
各类簇内的样本越相似,其与该类均值间的误差平方越小,对所有类所得到的误差平方求和,即可验证分为k类时,各聚类是否是最优的。
代码
spark2
Scala2.11
1.原生sparkcore
object KmeansTest { val k=2 //类个数 val dim=2 //数据集维度 val shold=0.0000000001 //阀值用于判断聚类中心偏移量 val centers=new Array[Vector[Double]](k) //聚类中心点(迭代更新) /** * 数据 * 1.658985, 4.285136 * -3.453687, 3.424321 * 4.838138, -1.151539 * -5.379713, -3.362104 * * @param sc * @return */ def loadDataSet(sc:SparkContext): Array[Vector[Double]] ={ val file = sc.textFile("") val res=file.map(t=>{ val value=t.split(" ").map(x=>{x.toDouble}) var vector = Vector[Double]() for(i <- 0 until dim) vector ++= Vector(value(i)) vector }).collect() res }
/** * * 随机初始化聚类中心 * k个聚类中心 * 初始化中心点如下: 3 Vector(-5.379713, -3.362104) 初始化中心点如下: 4 Vector(0.972564, 2.924086) * */ def initialCenters(points:Array[Vector[Double]]): Unit ={ val pointsNum=points.length val random = new Random() var index=0 var flag=true var temp=0 val array=new ListBuffer[Int] while(index < k){ val temp: Int = random.nextInt(pointsNum) flag=true if(array.contains(temp)){ flag=false }else{ if(flag){ array.append(temp) index+=1 } } }
for(i <- centers.indices){ centers(i)=points(array(i)) println("初始化中心点如下:") println(array(i)) println(centers(i)) } }
/** * 迭代做聚类 * @param points 随机下标 * @param centers 中心点 */ def kmeans(points:Array[Vector[Double]],centers:Array[Vector[Double]]): Unit = { var bool = true var newCenters = Array[Vector[Double]]() var move = 0.0 var currentCost = 0.0 //当前的代价函数值 var newCost = 0.0 //根据每个样本点最近的聚类中心进行groupBy分组,最后得到的cluster是Map[Vector[Double],Array[Vector[Double]]] //Map中的key就是聚类中心,value就是依赖于该聚类中心的点集 while(bool){//迭代更新聚类中心,直到最优 move = 0.0 // currentCost = computeCost(points,centers) val cluster = points.groupBy(v => closestCenter(centers,v))//聚类中心 newCenters = centers.map(oldCenter => { cluster.get(oldCenter) match {//找到该聚类中心所拥有的点集 case Some(pointsInThisCluster) => //均值作为新的聚类中心 vectorDivide(pointsInThisCluster.reduceLeft((v1,v2) => vectorAdd(v1,v2)),pointsInThisCluster.length) case None => oldCenter } }) for(i <- centers.indices){ //move += math.sqrt(vectorDis(newCenters(i),centers(i))) centers(i) = newCenters(i) } println("新的代价函数值:" + newCost) if(math.sqrt(vectorDis(Vector(currentCost),Vector(newCost))) < shold) bool = false newCost = computeCost(points,centers)//新的代价函数值 println("当前代价函数值:" + currentCost) }//while-end println("寻找到的最优中心点如下:") for(i <- centers.indices){ println(centers(i)) } } /** * 输出聚类结果 * @param points * @param centers */ def printResult(points:Array[Vector[Double]],centers:Array[Vector[Double]]): Unit = { //将每个点的聚类中心用centers中的下标表示,属于同一类的点拥有相同的下标 val pointsNum = points.length val pointsLabel = new Array[Int](pointsNum) var closetCenter = Vector[Double]() println("聚类结果如下:") for(i <- 0 until pointsNum){ closetCenter = centers.reduceLeft((c1,c2) => if (vectorDis(c1,points(i)) < vectorDis(c2,points(i))) c1 else c2) pointsLabel(i) = centers.indexOf(closetCenter) println(points(i) + "-----------" + pointsLabel(i)) }
}
/** * 找到某样本点所属的聚类中心 * @param centers * @param v * @return */ def closestCenter(centers:Array[Vector[Double]],v:Vector[Double]):Vector[Double] = { centers.reduceLeft((c1,c2) => if(vectorDis(c1,v) < vectorDis(c2,v)) c1 else c2 ) } /** * 计算代价函数(每个样本点到聚类中心的距离之和不再有很大变化) * @param points * @param centers * @return */ def computeCost(points:Array[Vector[Double]],centers:Array[Vector[Double]]):Double = { //cluster:Map[Vector[Double],Array[Vector[Double]] //类分组 val cluster = points.groupBy(v => closestCenter(centers,v)) //欧式距离 var costSum = 0.0
for(i <- centers.indices){ println(cluster.get(centers(i)).toBuffer) cluster.get(centers(i)) match{ case Some(subSets) => for(j <- subSets.indices){ costSum += (vectorDis(centers(i),subSets(j)) * vectorDis(centers(i),subSets(j))) } case None => costSum = costSum } } costSum } //--------------------------自定义向量间的运算----------------------------- //--------------------------向量间的欧式距离----------------------------- def vectorDis(v1: Vector[Double], v2: Vector[Double]):Double = { var distance = 0.0 for(i <- v1.indices){ distance += (v1(i) - v2(i)) * (v1(i) - v2(i)) } distance = math.sqrt(distance) distance } //--------------------------向量加法----------------------------- def vectorAdd(v1:Vector[Double],v2:Vector[Double]):Vector[Double] = { var v3 = v1 for(i <- v1.indices){ v3 = v3.updated(i,v1(i) + v2(i)) } v3 } //--------------------------向量除法----------------------------- def vectorDivide(v:Vector[Double],num:Int):Vector[Double] = { var r = v for(i <- v.indices){ r = r.updated(i,r(i) / num) } r }
def main(args: Array[String]): Unit = { val sparkConf = new SparkConf().setMaster("local[2]").setAppName("KmeansTest") val sc=new SparkContext(sparkConf) val rows=loadDataSet(sc) //ArrayBuffer(Vector(1.658985, 4.285136), Vector(-3.453687, 3.424321), // Vector(4.838138, -1.151539), Vector(-5.379713, -3.362104)) initialCenters(rows)
/** * 寻找到的最优中心点如下: Vector(-2.3914716666666664, 1.4491176666666667) Vector(4.838138, -1.151539) 聚类结果如下: Vector(1.658985, 4.285136)-----------0 Vector(-3.453687, 3.424321)-----------0 Vector(4.838138, -1.151539)-----------1 Vector(-5.379713, -3.362104)-----------0 */ kmeans(rows,centers) printResult(rows,centers) } }
2.sparkmllib
object KmeansTest2 { def main(args: Array[String]): Unit = { val sparkConf=new SparkConf().setAppName("KmeansTest2").setMaster("local[2]") val sc=new SparkContext(sparkConf)
val data=sc.textFile("")
val parsedData=data.map(s=>Vectors.dense(s.split(" ").map(_.toDouble)))
val numClusters=2 val numIterations=30 val model=KMeans.train(parsedData,numClusters,numIterations)
// 数据模型的中心点 println("Cluster centres:") for(c <- model.clusterCenters) { println(" " + c.toString) }
// 使用误差平方之和来评估数据模型 val cost = model.computeCost(parsedData) println("Within Set Sum of Squared Errors = " + cost)
// 使用模型测试单点数据 /*println("Vectors 7.3 1.5 10.9 is belong to cluster:" + model.predict(Vectors.dense("1.5 10.9".split(" ") .map(_.toDouble)))) println("Vectors 4.2 11.2 2.7 is belong to cluster:" + model.predict(Vectors.dense("11.2 2.7".split(" ") .map(_.toDouble)))) println("Vectors 18.0 4.5 3.8 is belong to cluster:" + model.predict(Vectors.dense("14.5 73.8".split(" ") .map(_.toDouble))))*/
// 返回数据集和结果 val result = data.map { line => val linevectore = Vectors.dense(line.split(" ").map(_.toDouble)) val prediction = model.predict(linevectore) line + " " + prediction }.collect.foreach(println)
sc.stop
} }