这是我参与8月更文挑战的第19天,活动详情查看:8月更文挑战
这个正规方程是放在多元线性回归里边讲的。之前线性回归我们讲的是梯度下降,循环执行一个公式逐步下降,而正规方程与之相反,是直接对θ求最优解。基本上只需一步就可以完成。
什么是正规方程?
先举个简单的例子:
Intuition:
If 1D(θ∈R)
J(θ)=aθ2+bθ+c
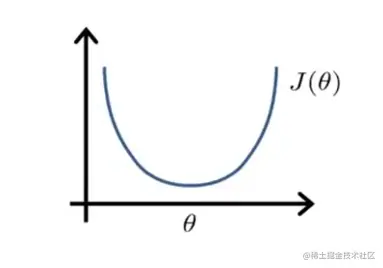
现在假设θ只是一个实数,不是向量,函数J是关于θ的一个二次函数。
对这个函数求最小值,怎么一步实现?只要你学过高中数学就会知道:求导。求出dxdh(x)=0那个x就是符合是函数最小化的值。
但是一般我们接触到的并不是这种函数,取值范围都是向量。在梯度下降中是循环执行对每一个θ求偏导,最后求出何时θ=0,那现在我们就可以直接求出等于0的这一步。
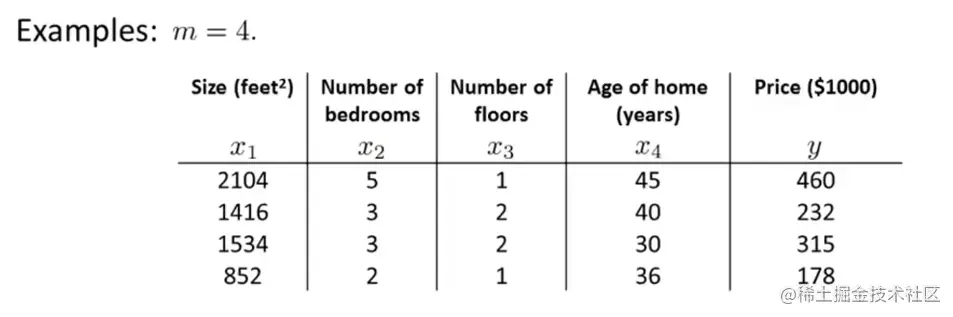
现在我们有一个训练样本,在数据集中加上一列x0=1把这个训练集变成一个系数矩阵:
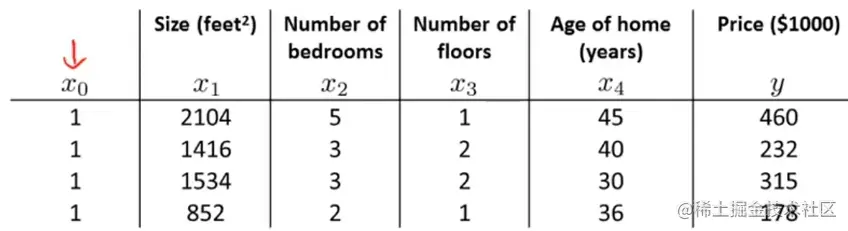
X=⎣⎡11112104141615348525332122145403036⎦⎤
同样把y列成一个向量:
y=⎣⎡460232315178⎦⎤
矩阵X包含了所有的特征量,是一个m*n+1的矩阵,y是一个m维矩阵。m是训练样本的数量。
现在只需要一步:θ=(XTX)−1XTy即可求出最优解。
Set theta to be equal to X transpose X inverse times X transpose y, this would give you the value of theta that minimizes your cost function.
特征量矩阵的转置乘自身,然后求逆,之后再乘特征量矩阵的转置,然后再乘y向量。
所以正规方程就是:
m examples ((x1,y1),...,(xn,yn))
,n features.
假设现在我们的训练集有m个训练样本。一共有n个特征量。那特征量x的向量就是
x=⎣⎡x0ix1ix2i...xni⎦⎤∈Rn+1
而将x转化为矩阵X就变成
X=⎣⎡...(x0i)T......(x1i)T......(x2i)T.........(xni)T...⎦⎤∈Rm×n+1
而y则是:
y=⎣⎡y1y2y3...ym⎦⎤∈Rm
列出Xy以后:
θ=(XTX)−1XTy
在octave中只需要一句pinv(X' * X) * x' * y
并且这种方法也不需要进行特征量缩放。
如果XTX矩阵不可逆怎么办?
其实在octave中,有两个求逆矩阵的方法,一个pinv()一个inv()。用前者,即使矩阵不可逆,你也可以得到卒子红正确的θ值。
可逆矩阵 AB = BA = I,对于矩阵A,能找到一个矩阵B与其相乘,使结果等于单位矩阵,那矩阵A就是可逆矩阵。
一般来说你遇到的不可逆矩阵有两情况:
-
有多余的特征量
比如给你
x1=sizeinfeet2x2=sizeinm2
一个面积单位是平方英尺,一个面积单位是平方米。这种情况下你可以舍弃一个特征量。
-
特征量过多(m<=n)
这种情况下删除某些特征量或者进行正则化。
正则化之后会讲到。
我有个不成熟的想法:为什么不可以将m循环一下,使其称为一个方阵哈哈哈哈哈,就比如⎣⎡a11,a12,a13,a14,a15a21,a22,a23,a24,a25a31,a32,a33,a34,a35a11,a12,a13,a14,a15a21,a22,a23,a24,a25⎦⎤
对比正规方程和梯度下降
| Gradient descent | Normal equation |
|---|
Need to choose α
Needs many iterations | No need to choose α
Don't need to iterate |
| Works well even when n is large. | Need to compute(XTX)−1, Slow if n is very large
The normal equation method actually do not work for some more sophisticated learning algorithms. |
- 梯度下降:
- 正规方程:
- 优点:
- 不需要选择α
- 不需要多迭代
- 不先不要考虑取值范围进行缩放
- 缺点:
- 需要计算(XTX)−1而两个矩阵相乘,复杂度数量级是O(n3)所以数据量比较大的时候运行会很慢
- 对于一些复杂算法程无法使用
总结
数据量小的简单算法使用正规方程更迅速。数据量大或者算法更为复杂还是需要使用梯度下降。