18-19（1.2.1 概率密度）1.2.1 概率密度除了考虑在离散时间集上定义的概率外，我们还希望考虑关于连续变量的

1.2.1 概率密度

除了考虑在离散时间集上定义的概率外，我们还希望考虑关于连续变量的概率。我们将仅限于相对非正式的讨论。如果实值变量 $x$ 落在区间 $(x,x+\delta x)$ 内的概率由 $p(x)\delta x$ 表示 $\delta x\rightarrow 0$ ，那么 $p(x)$ 称为 $x$ 上的概率密度。如图1.12所示。 $x$ 位于区间 $(a,b)$ 内的概率由下式给出：

p(x\in(a,b))=\int_a^bp(x)dx\tag{1.24}

因为概率是非负的，并且因为 $x$ 的值必须位于实轴的某个位置，所以概率密度 $p(x)$ 必须满足这两个条件

p(x)\geq0\tag{1.25}

\int_{-\infty}^\infty p(x)dx=1\tag{1.26}

在变量的非线性变化下，由于雅可比因子，概率密度变换不同与简单函数。例如，如果我们考虑变量 $x=g(y)$ 的变化，那么函数 $f(x)$ 变为 $f(y)=f(g(y))$ 。现在考虑概率密度 $p_x(x)$ ，其对应于相对于新的变量 $y$ 的密度 $p_y(y)$ ，其中足够表示 $p_x(x)$ 和 $p_y(y)$ 是不同密度的事实。对于较小的 $\delta x$ 的值，位于 $(x,x+\delta x)$ 范围内的观测值将转换为 $(y,y+\delta y)$ 范围，其中 $p_x(x)\delta x \simeq p_y(y)\delta y$ ，因此

P(z)=\int_{-\infty}^zp(x)dx\tag{1.28}

它满足 $P'(x)=p(x)$ ，如图1.12所示。

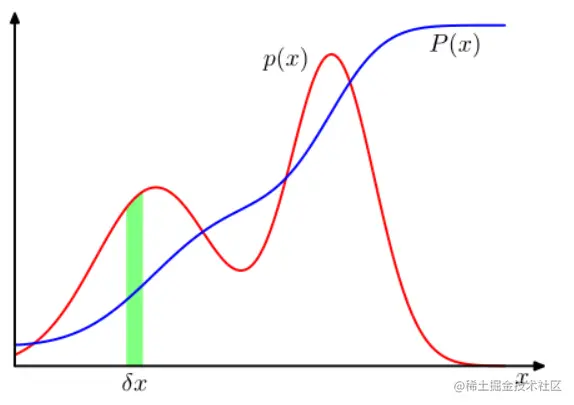
Figure 1.12

图 1.12 离散变量的概率概率可以扩散为连续变量 $x$ 上的概率密度 $p(x)$ ，并且使得位于区间 $(x,\delta x)$ 的 $x$ 的概率由 $\delta x$ 的 $p(x)\delta x$ 给出 $\delta x\rightarrow0$ 。概率密度可以表示为累计分布函数 $P(x)$ 的导数。

如果我们有几个连续变量 $x_1,...,x_D$ ，用向量 $x$ 表示，那么我们可以定义联合概率密度 $p(x)=p(x_1,...,x_D)$ 使得x落入包含点 $x$ 的无穷小体积 $\delta x$ 中的概率由 $p(x)\delta x$ 给出。这个多元概率密度必须满足

p(x)\geq0\tag{1.29}

\int p(x)dx=1\tag{1.30}

其中的积分是对整个 $x$ 空间的积分。我们也可以考虑联合概率分布在离散变量和连续变量上的组合上。

注意，如果 $x$ 是一个离散变量，那么 $p(x)$ 有时被称为概率质量函数，因为它可以视为一组集中在 $x$ 允许值处的 “概率质量”。

概率和积规则以及贝叶斯定理同样适用于概率密度的情况，或离散变量和连续变量的组合。例如，如果 $x$ 和 $y$ 是两个实变量，那么求和规则和乘积规则的形式为

p(x)=\int p(x,y)dy\tag{1.31}

p(x,y)=p(y|x)p(x)\tag{1.32}

连续变量和积规则的形式证明需要一个称为测量理论的数学分支，不在本书的范围内。然而，通过将每个实变量划分为宽度区间，可以非正式地看出它的有效性 $\Delta$ 考虑这些区间上的离散概率分布。走极限 $\Delta\rightarrow0$ 然后将求和转换为积分并给出所需的结果。