这是我参与8月更文挑战的第13天，活动详情查看：8月更文挑战

本文为吴恩达机器学习课程的笔记系列第七篇，主要学习异常检测算法。

异常检测(Anomaly Detection)

异常检测属于非监督问题。异常检测是机器学习算法的一个常见应用，是对不匹配预期模式或数据集中其他项目的项目、事件或观测值的识别。简单来说，当正样本比较多时，通过对正样本的学习，机器学会正样本的特征，从而对异常样本有了识别能力。

异常检测的核心就在于找到一个概率模型，帮助我们知道一个样本落入正常样本中的概率，从而帮助我们区分正常和异常样本。

高斯分布

高斯分布模型是异常检测中常用的概率模型。其概率密度函数如下：

$p(x,\mu,\sigma^2)=\dfrac{1}{\sqrt{2\pi}\sigma}exp(-\dfrac{(x-\mu)^2}{2\sigma^2})$

其中：

• $\mu=\dfrac{1}{m}\sum\limits_{i=1}^{m}x^{(i)}$
• $\sigma^2=\dfrac{1}{m}\sum\limits_{i=1}^{m}(x^{(i)}_j-\mu_j)^2$

应用到异常检测算法，对于$m$ 个样本的数据集，针对每一个特征，进行参数估计：

• $\mu_j=\dfrac{1}{m}\sum\limits_{i=1}^{m}x^{(i)}_j$
• $\sigma^2_j=\dfrac{1}{m}\sum\limits_{i=1}^{m}(x^{(i)}-\mu)^2$

假设每个样本有$n$个特征，即 $x_i$ 变成一个 $n$ 维的向量 $\begin{bmatrix}x_i^{(1)}\\x_i^{(2)}\\ \vdots \\x_i^{(n)}\end{bmatrix}$

对于一个训练实例，有：

$p(x)=\prod\limits_{j=1}^{n}(x_j,\mu,\sigma^2)=\prod\limits_{j=1}^{n}\dfrac{1}{\sqrt{2\pi}\sigma}exp(-\dfrac{(x-\mu)^2}{2\sigma^2})$

如何判断样本是否异常？

我们选择一个$\epsilon$，将 $p(x)=\epsilon$ 作为我们的判定边界，当 $p(x)>\epsilon$ 时预测数据为正常数据，否则为异常。

异常检测与有监督学习对比

异常检测	有监督学习
数据非常偏斜，非常少量的正向类（异常数据$y=1$ ）, 大量的负向类（$y=0$）	数据分布均匀，同时有大量的正向类和负向类
异常的类型不一，很难根据对现有的异常数据（即正样本）来训练算法。	有足够多的正样本，可以根据对正样本的拟合来知道正样本的形态，从而预测新来的样本是否是正样本。
未来遇到的异常可能与已掌握的异常、非常的不同。	未来遇到的正向类实例可能与训练集中的非常近似。
例如： 欺诈行为检测 生产（例如飞机引擎）检测数据中心的计算机运行状况	例如：邮件过滤器 天气预报 肿瘤分类

特征选择

我们使用异常检测算法时，是假设数据集特征符合高斯分布的。但有时候数据集可能像下图左边一样，这时直接用异常检测算法也是可以得出结果，但一般我们可以对数据进行一些转换如取对数操作，将其转换为高斯分布。

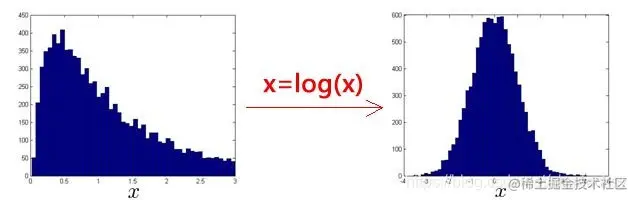
误差分析

有时候，我们可能发现某个异常样本的$p(x)$ 值高于$\epsilon$，我们对此进行分析，观察是哪些异常数据被预测为正常。下面以监测机房中的服务器异常为例：

假设我们选取如下特征：

$x_1=网络流量；x_2=CPU负载$

当出现一个异常：CPU负载很高，而网络流量很低，服务器卡死，无法通信。如下图：

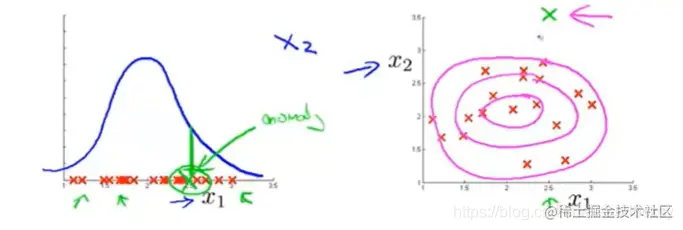
此时的$p(x)$ 值也会很高，为了识别这一异常状况，我们可以构建新的特征：$x_3=\dfrac{CPU负载}{网络流量}$ ，当上述异常发生时，这个特征便会变得很大，有利于我们识别出来。

多元高斯分布

一般的高斯模型因为是同时累乘每个特征的偏差，所以会创造出一个较大的判定边界。

模型定义：

$p(x,\mu,\Sigma)=\dfrac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}exp(-\dfrac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))$

• $\mu=\dfrac{1}{m}\sum\limits_{i=1}^{m}x^{(i)}$
• $\Sigma=\dfrac{1}{m}\sum\limits_{i=1}^{m}(x^{(i)}-\mu)(x^{(i)}-\mu)^T=\dfrac{1}{m}(X-\mu)^T(X-\mu)$

其中，$\mu$ 是一个向量，表示样本均值，$\Sigma$ 表示样本协方差矩阵。

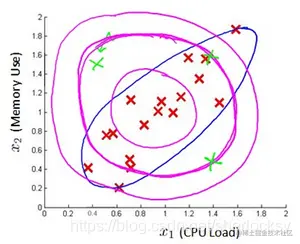
先考虑各个维度不相关，各个维度之间不相关的多元正态分布概率密度其实就是各个维度的正态分布概率密度函数的乘积，其实是因为各变量之间互不相关，因此联合概率密度等于各自概率密度的乘积。

右边项：

如果各个维度是相关的，那怎么办呢？

实际上我们可以利用化归的思想，把相关变成不相关，

方向变换：$u_1=\begin{bmatrix}u_1^{(1)}\\u_1^{(2)} \end{bmatrix}, u_2=\begin{bmatrix}u_2^{(1)}\\u_2^{(2)} \end{bmatrix}$，使得各个维度之间不相关，下面是推导：

最后的概率：

应用到异常检测的算法，首先对各个样本进行参数估计：

• $\mu=\dfrac{1}{m}\sum\limits_{i=1}^{m}x^{(i)}$
• $\Sigma=\dfrac{1}{m}\sum\limits_{i=1}^{m}(x^{(i)}-\mu)(x^{(i)}-\mu)^T$

当新样本$x$到来时，计算$p(x)$：

$p(x)=\dfrac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}exp(-\dfrac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))$

多元高斯分布与一般高斯分布对比

一般高斯分布模型：$p(x)=p(x_1,\mu_1,\sigma_1^2)\times p(x_2,\mu_2,\sigma_2^2)\times ...\times p(x_n,\mu_n,\sigma_n^2)$

可见一般高斯模型是多元高斯模型的一个特例，也就是当协方差矩阵 $\Sigma$ 的上三角和下三角为$0$的时候。即$\Sigma=\begin{bmatrix}\sigma_1^2&0&...&0\\0&\sigma_2^2&...&0\\0&0&\ddots&0\\0&0&...&\sigma_n^2\end{bmatrix}$

两者的区别：

一般高斯分布模型	多元高斯分布模型
需要创建一些特征（比如组合$x_1,x_2$）来描述某些特征的相关性	自动描述了各个特征的相关性
计算复杂度低，适于高维特征	计算较复杂，计算量大
即使样本数$m$较小也适用	必须满足$m>n$，且各个特征必须线性无关，否则协方差矩阵将不可逆