聚类(Clustering)

聚类(Clustering)是将数据集划分为若干相似对象组成的多个组(group)或簇(cluster)的过程，使得同一组中对象间的相似度最大化，不同组中对象间的相似度最小化。属于无监督问题。

K-Means算法

$K$ 就是簇的数量。这个数字是人为选择的。K-Means算法是基于质心划分的。

算法流程：

首先随机选择 $K$ 个点作为初始聚类中心。
对数据集的每个数据，评估其到 $K$ 个中心点的距离，将其与距离最近的中心点关联起来。
重新计算每个簇中的平均值，更新簇中心的位置

距离的判断：欧几里得距离或余弦相似度

算法描述：

$\mu^{(i)}$ 表示第 $i$ 个聚类中心， $x^{(i)}$ 表示第 $i$ 个样本， $m$ 表示样本数

\begin{aligned} &Repeat \{ \\ & \;\; for\; i =\; 1\; to\; m:\\ &\qquad c^{(i)} := 与样本x^{(i)}最近的簇中心的索引 \\ &\;\;for\; k =\; 1\; to\; K: \\ &\qquad \mu^{(k)}:= 第k个簇的平均位置 \\ &\} \end{aligned}

算法优化

K-Means同样也要最小化聚类代价，而最小化的就是所有的数据点与其所关联的聚类中心点之间的距离之和，引入K-Means的代价函数：

$J(c^{(1)},...,c^{(m)},\mu^{(1)},...,\mu^{(K)})=\dfrac{1}{m}\sum\limits_{i=1}^{m}||x^{(i)}-\mu^{c^{(i)}}||^2$ $J$ 也称畸变函数（Distortion Function）

实际上，在第一个for循环里，也就是给样本分配簇中心时，就是在减小 $c^{(i)}$ 引起的代价；在第二个for循环里，则是在减小 $\mu^{(k)}$ 引起的代价。

确定k值

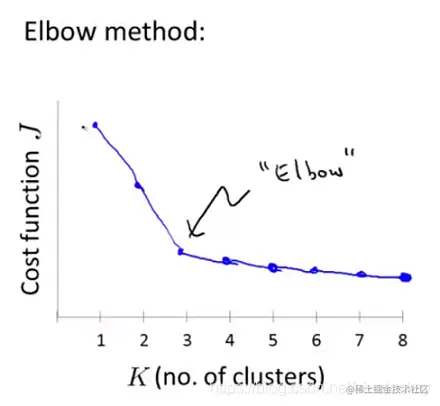
因为不同的初始化很有可能会引起不同的聚类结果，所以应用聚类算法时往往进行多次随机初始化，计算相应代价函数，应用 肘部法则（Elbow Method），选择较为明显的“肘关节”部分对应的 k 值作为聚类数。如下图：

在这里插入图片描述

下面补充几个其它常见的聚类算法：

二分K-Means算法

二分 K-Means（bisecting kmeans）算法，相较于常规的 K-Means，二分 K-Means 不急于一来就随机 K个聚类中心，而是首先把所有点归为一个簇，然后将该簇一分为二。计算各个所得簇的代价函数（即误差），选择误差最大的簇再进行划分（即最大程度地减少误差），重复该过程直至达到期望的簇数目。

误差采用 SSE（Sum of Squared Error）即误差平方和。SSE越小，簇中的对象越集中。

该算法为贪心算法，计算量不小。

DBSCAN算法

DBSCAN算法是基于密度的算法，该算法将具有足够高密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇，它将簇定义为密度相连的点的最大的集合。

基本概念：

$Eps$ 邻域：给定对象半径 $Eps$ 内的邻域称为该对象的 $Eps$ 邻域。
$MinPts$ ：给定邻域包含的点的最小数目，用以决定点 $p$ 是簇的核心部分还是边界点或噪声。
核心对象：如果对象的 $Eps$ 邻域包含至少 $MinPts$ 个的对象，则称该对象为核心对象。
边界点：边界点不是核心点，但落在某个核心点的邻域内。稠密区域边缘上的点。
噪音点：既不是核心点，也不是边界点的任何点。稀疏区域中的点。
直接密度可达：如果 $p$ 在 $q$ 的 $Eps$ 邻域内，而 $q$ 是一个核心对象，则称对象 $p$ 从对象 $q$ 出发时是直接密度可达的 (directly densityreachable)。
密度可达：如果存在一个对象链 $p_1,p_2,...,p_n,p_1=q,p_n=p$ ，对于 $p_i\in D(1\le i\le n)$ ， $p_{i+1}$ 是 $p_i$ 从关于 $Eps$ 和 $MinPts$ 直接密度可达的，则对象 $p$ 是从对象 $q$ 关于 $Eps$ 和 $MinPts$ 密度可达的 (densityreachable)。
密度相连：如果存在对象 $O\in D$ ，使对象 $p$ 和 $q$ 都是从 $O$ 关于 $Eps$ 和 $MinPts$ 密度可达的，那么对象 $p$ 到 $q$ 是关于 $Eps$ 和 $MinPts$ 密度相连的(density-connected)。
基于密度的簇：是基于密度可达性的最大的密度相连的对象的集合。
噪声：不包含在任何簇中的对象。

DBSCAN算法，就是检查数据集中每个点的 $Eps$ 邻域来搜索簇。

算法流程

\begin{aligned} &(1) \text{首先将数据集}D中的所有对象标记为未处理状态 \\ &(2) for\;数据集D中每个对象p \;do \\ &(3) \quad if \;p已经归入某个簇或标记为噪声\;then\\ &(4) \qquad continue;\\ &(5) \quad else\\ &(6) \qquad 检查对象p的Eps邻域 E(p); \\ &(7) \qquad \quad if \;E(p)包含的对象数小于MinPts \;then \\ &(8) \qquad \qquad 标记对象p为边界点或噪声点；\\ &(9) \qquad \quad else\\ &(10) \qquad \qquad 标记对象p为核心点，并建立新簇C；\\ &(11) \qquad \qquad for\; E(p)中所有尚未被处理的对象q\; do\\ &(12) \qquad \qquad \quad 检查其Eps邻域E(p)，若E(p)包含至少MinPts个对象，则将E(p) 中未归入任何一个簇的对象加入C \end{aligned}

算法优劣

优势：

不需要指定簇个数
擅长找到离群点（检测任务）
可以发现任意形状的簇
只需两个参数

劣势：

参数难以选择（参数对结果的影响非常大）
高维数据有些困难（可以做降维）

机器学习入门之聚类算法